Передача тепла через однослойную стенку
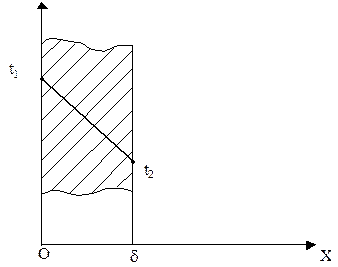
Стационарное температурное поле в однослойной плоской стенке.
Распределение температуры по толщине стенки является линейным – уравнение имеет вид:
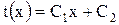
где 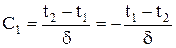 ;
;
С2=t1
Таким образом, искомое распределение температуры по толщине стенки имеет вид:
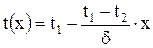
Плотность теплового потока, проходящего через стенку определяем, используя уравнение Фурье:
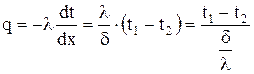 ,
,
где 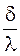 – термическое сопротивление.
– термическое сопротивление.
Передача тепла через многослойную стенку.
Стены металлургических печей и других нагревательных устройств обычно выкладывают из различных огнеупоров, в несколько слоев: три, четыре и более.
Стационарное температурное поле в многослойной стенке:

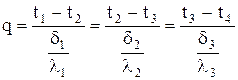
d1, d2, d3 – толщина слоев;
l1, l2, l3, – коэффициенты теплопроводности материалов слоев;
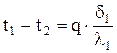 ;
; 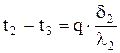 ;
; 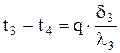 .
.
Складывая, левые и правые части получим:
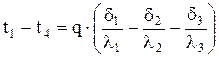 ;
;
или
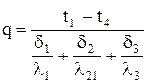
Лекция 9:
Передача тепла конвекцией
Общие сведения
Явление конвекции заключается в переносе тепла движущимися объемами газа или жидкости. Одновременно с конвекцией в газах осуществляется перенос тепла теплопроводностью. В технике часто встречаются конвективный теплообмен газа или жидкости с поверхностью твердых тел. Например при работе обогревателя: воздух соприкасается с горячей поверхностью нагревателя, плотность уменьшается, поднимается вверх; на его место поступают новые холодные объемы воздуха.
Величина теплового потока Q, обусловлена конвективным теплопереносом, определяется законом Ньютона:
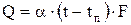 ,
,
где a – коэффициент теплопередачи конвекцией, вт/(м2*град), ккал/(м2*ч*град);
t – температура источника тепла;
tп – температура омываемой теплоносителем поверхности,
F – площадь поверхности теплообмена.
Удельный тепловой поток при конвективном теплообмене:
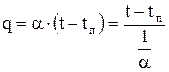
где 1/a – термическое сопротивление теплоотдачи или внешнее тепловое сопротивление.
Внешний теплообмен конвекций связан с омыванием газом поверхности нагрева или охлаждения. Тепловой поток при передачи конвекцией определяется по формуле Ньютона:
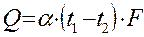 , Вт, (1)
, Вт, (1)
где α – коэффициент теплоотдачи, 
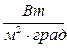
t1 – температура теплоотдающей среды (твердого тела при его охлаждении, газа – при нагреве)
t2 – температура тепловоспринимающей среды (твердого тела – при его нагреве, газа или жидкости – при охлаждении), С
Удельный тепловой поток равен:
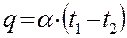 ,
, 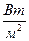 (2)
(2)
Для определения коэффициентов теплоотдачи α обычно пользуются экспериментальными формулами, разработанными на основе теории подобия критериальном виде. Определяемым в этих формулах является критерий Нуссельта:
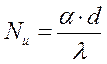 , (3)
, (3)
где d – линейный размер твёрдого тела, м;
λ – коэффициент теплопроводности среды, 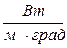
Определяющий критерий зависит от характера движения (свободное или вынужденное) и режимы движения (ламинарное или турбулентное).
Свободная конвекция.
Внешний теплообмен свободной конвекцией возникает при свободном движении газа у нагретой или охлажденной поверхности, обусловленном разной плотностью среды при наличии разности температур (неравномерном температурном поле).
Например, теплоотдача свободной конвекцией имеет место при охлаждении на воздухе горячего металла, при передачи тепла в окружающую среду наружной поверхностью кладки печей и т.д.
Для определения коэффициента теплоотдачи при свободной конвекции пользуются следующими зависимостями:
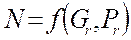 . (4)
. (4)
Здесь Gr – критерий Просгофа;
Pr – критерий Прандтля.
Критерий Просгофа:
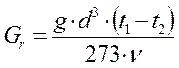 , (5)
, (5)
гдеg = 9,81 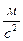 – ускорение силы тяжести;
– ускорение силы тяжести;
d–определяющий размер тела, м;
t1 и t2 - температура соответственно греющей и нагреваемой среды, С;
υ– коэффициент кинематической вязкости газа, 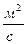
Критерий Прандтля:
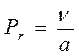 , (6)
, (6)
где а – коэффициент температуропроводности, 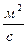
Расчетная формула для определения коэффициента теплоотдачи α в критериальном виде имеет вид:
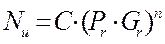 , (7)
, (7)
В формуле (7) физические величины отнесены к средней температуре:
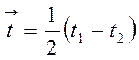 .
.
а) при: 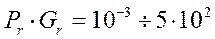
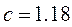
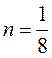
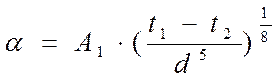 ,
, 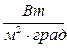 (8)
(8)
б) при: 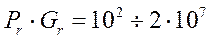
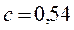
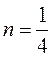
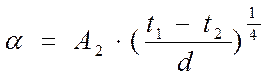 ,
, 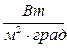 (9)
(9)
в) при: 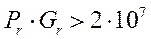
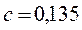
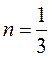
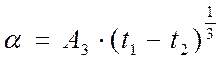 ,
, 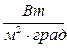 (10)
(10)
Значение коэффициентов А находят из справочных таблиц.
В формулах (8), (9) и (10) приняты следующие линейные размеры тела: для шара и горизонтальных труб – их диаметр, для вертикальных труб и плит – высота омываемого участка, для горизонтальных плит – их наименьшая длина.
3. Вынужденная конвекция при продольном обтекании поверхности.
Продольная или поперечная обтекания твердой поверхности играют большую роль, например, при нагреве воздуха в трубчатых или блочных рекуператорах. Определяющим критерием конвективного теплообмена является критерием Рейнольдса:
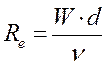 ;
;
где W – скорость движения потока при действительных условиях, м/с;
d – диаметр канала, м;
υ - коэффициент кинематической вязкости 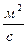 .
.
При вынужденном ламинарном движении на условия теплообмена оказывает влияние также свободное движение, в связи, с чем в этом случае учитывается и критерий Gr.
При ламинарном движении газа в каналах различного сечения (Re ≤ 2100):
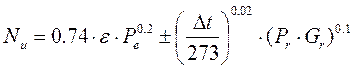 (11)
(11)
где ε – коэффициент, зависящий от отношения L/d, определяется по справочным таблицам;
∆t = t1 - t2 - температурный напор, С;
Pe – критерий Пекле; Pe = Wd/a; W – скорость потока, м/с; d – диаметр канала, м; a – коэффициент теплопроводности среды, 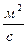 .
.
В формуле (11) знак «+» относится к совпадению направления свободного и вынужденного движения, знак «−» при противоположных направлениях.
Физические величины в формуле (11) должны быть отнесены к средней температуре:
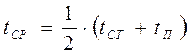 ,
,
где tст – температура стенки, С;
tп – средняя температура потока, С.
При турбулентном движении газа (Re ≥ 2300):
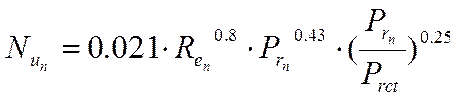
| (12) |
При переходном движении газа:
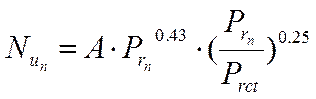 .
.
Значение коэффициента А = f (Re) в зависимости от Re определяют по справочным таблицам.
Выражение (Prn/ Prст) для газов близко к единицы.
В каналах не круглого сечения в качестве диаметра канала применяется эквивалентный диаметр dэкв = 4F/П, где F- площадь канала; П – периметр; в случае круглого канала – о обычный диаметр d = 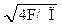
4) Вынужденная конвекция при поперечном обтекании труб и цилиндров.
При поперечном обтекании одиночной трубы или цилиндра и Ren = 10 ÷ 1000 коэффициент теплоотдачи конвекцией определяется из формулы:
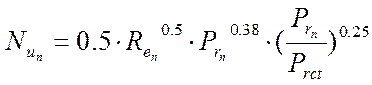 |
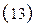 |
При расчете рекуператоров большое значение имеет теплообмен в пучках труб.
Расположение пучков труб рекуператорах чаще всего бывает коридорное и шахматное.
При Ren = 2·100 ÷ 2·100000 формулы для определения критерия Нуссельта следующие:
а) для коридорных пучков:
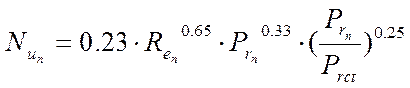 |
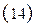 |
б) для шахматных пучков:
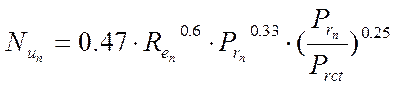 |
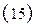 |
В формулах (14) и (15) в качестве определяющего размера принимают наружный диаметр труб.
Лекция 10:
Излучение твердых тел
