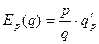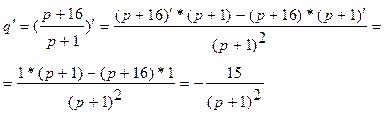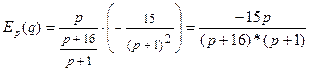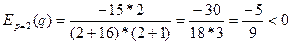Тема 1. «Пределы числовых последовательностей и функций»
Красноярск 2016
Составители: доцент Л.М. Коренюгина,
старший преподаватель Е.С. Разгулина
Коренюгина Л.М., Разгулина Е.С.
МаТЕМАТИЧЕСКИЙ АНАЛИЗ: Практические задания по дисциплине для студентов очной формы обучения направления 38.03.01 Экономика
/ Л. М. Коренюгина, Е. С. Разгулина. – Красноярск: АНО ВО СИБУП, 2016. – с.
Все темы сопровождаются расчётными примерами с обстоятельными пояснениями. Предложены варианты выполнения контрольной работы.
Методические указания утверждены и одобрены к печати научно–методическим советом СИБУП от 2016 г. Протокол №
Коренюгина Л. М., Разгулина Е. С., 2016
АНО ВО Сибирский институт бизнеса, управления и психологии, 2016
Содержание
ВВЕДЕНИЕ 4
Тема 1. «Пределы числовых последовательностей и функций». 5
Тема 2: «Дифференциальное исчисление функции одной переменной». 17
Тема 3: «Дифференциальное исчисление функции нескольких переменных» 29
Тема 4: «Интегральное исчисление». 41
Тема 5: «Дифференциальные уравнения». 50
Тема 6: «Ряды». 85
Итоговая контрольная работа №1 по темам 1,2,3. 96
Итоговая контрольная работа №3 по теме 5. 102
СПИСОК ЛИТЕРАТУРЫ... 104
ВВЕДЕНИЕ
Тема 1. «Пределы числовых последовательностей и функций»
Пример1.1
Найти область определения функции, исследовать заданную функцию на чётность.
1. a) f(x)= arctg( 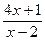 ); b) f(x)=
); b) f(x)= 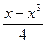 -ctg(2x);
-ctg(2x);
Решение:
А)) f(x)= arctg( 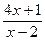 );
);
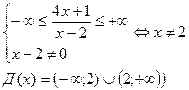
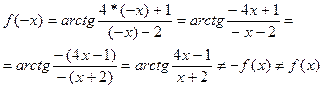
b) f(x)= 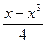 -ctg(2x);
-ctg(2x);
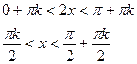
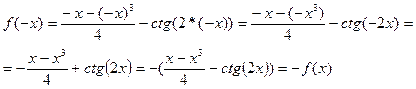
Пример1.2.
Найти предел
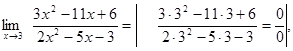 Здесь мы имеем с неопределенностью вида
Здесь мы имеем с неопределенностью вида 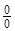 .
.
Разложим в числителе данное выражение на множители
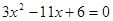
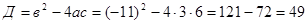
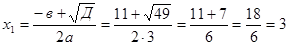
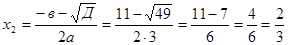
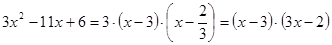
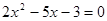
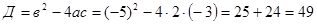
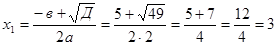
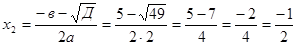
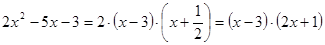
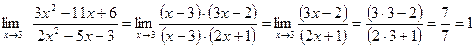
Пример1.3.
Найти предел
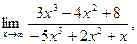 Здесь мы имеем с неопределенностью вида
Здесь мы имеем с неопределенностью вида 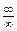 . Разделим числитель и знаменатель данной дробно-рациональной функции на
. Разделим числитель и знаменатель данной дробно-рациональной функции на 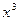 (на x в наивысшей степени). Тогда используя свойства пределов, получим
(на x в наивысшей степени). Тогда используя свойства пределов, получим
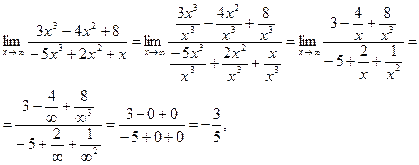
Пример1.4.
Найти предел
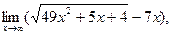
Здесь мы имеем с неопределенностью вида ¥–¥. Умножим и разделим данное выражение на точно такое же, но со знаком плюс между слагаемыми (на сопряженное выражение):
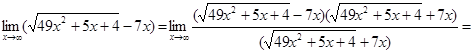
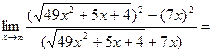
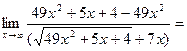
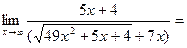
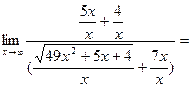
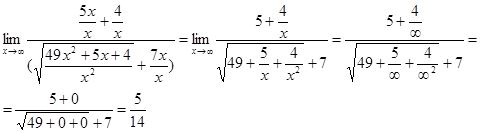
Пример1.5.
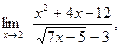
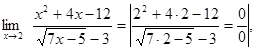
Здесь мы имеем с неопределенностью вида 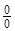 . Умножим числитель и знаменатель на точно такое же выражение, стоящее в знаменателе, но со знаком плюс между слагаемыми:
. Умножим числитель и знаменатель на точно такое же выражение, стоящее в знаменателе, но со знаком плюс между слагаемыми:
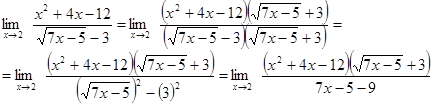
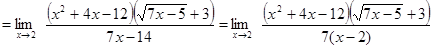
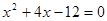
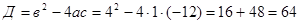
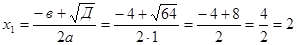
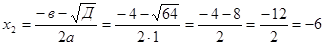
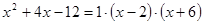
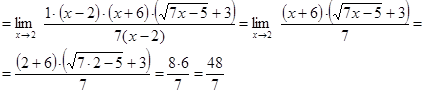
Пример1.6.
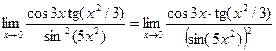 Здесь мы имеем с неопределенностью вида
Здесь мы имеем с неопределенностью вида 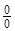 . При вычислении данного предела воспользуемся методом эквивалентных бесконечно малых величин.
. При вычислении данного предела воспользуемся методом эквивалентных бесконечно малых величин.
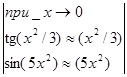 =
= 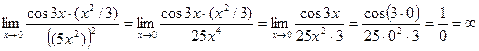 Пример1.7.
Пример1.7.
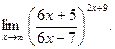 Здесь мы имеем с неопределенностью вида
Здесь мы имеем с неопределенностью вида 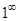 . Преобразуем выражение, стоящее в скобках, следующим образом
. Преобразуем выражение, стоящее в скобках, следующим образом
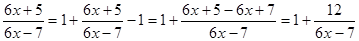 .
.
Тогда исходный предел можно преобразовать так:
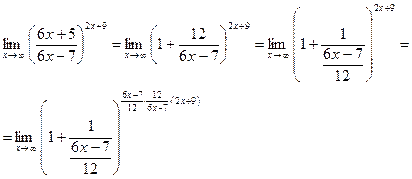
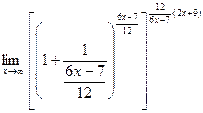
Предел выражения в квадратных скобках, в соответствии со вторым замечательным пределом, равен
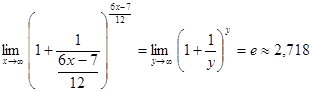 .
.
В результате получаем
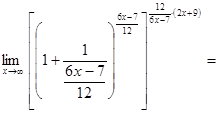
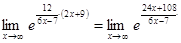
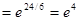 .
.
Пример1.8.
Вычислить пределы функций, не пользуясь правилом Лопиталя.
a ) 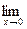
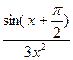 ; b )
; b ) 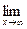
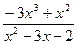 ; c )
; c ) 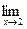
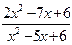 ;
;
d ) 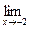
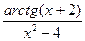 ;
;
Решение:
а) 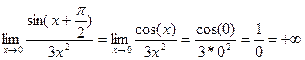 ;
;
b ) 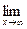
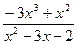
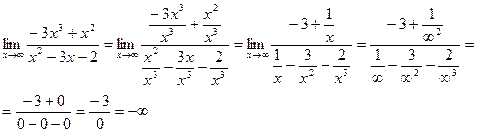 ;
;
c ) 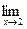
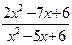 ;
;
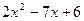 =0
=0
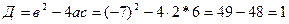
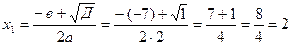
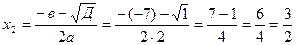
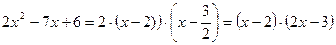
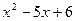 =0
=0
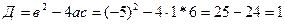
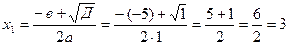
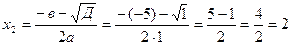
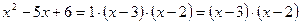
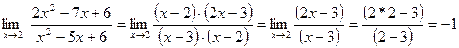
d ) 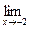
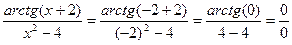
Здесь мы имеем с неопределенностью вида 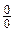 .
.
При вычислении данного предела воспользуемся методом замены и методом эквивалентных бесконечно малых величин.
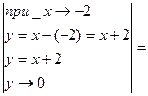
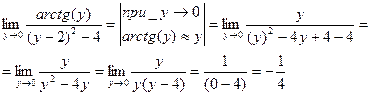

Пример 1.9.
Задана функция y=f(x) и два значения аргумента x 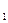 и x
и x 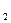 . Требуется:
. Требуется:
1) найти область непрерывности функции и установить, является ли данная функция непрерывной для каждого из заданных значений аргумента;
2) в случае разрыва функции сделать вывод о характере точки разрыва;
3) сделать схематический чертёж в окрестности точки разрыва.
f(x)= 12 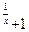 , x
, x 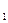 = 1 , x
= 1 , x 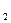 = 0 ;
= 0 ;
Данная функция элементарная
1) Область определения
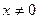
Д(х)= 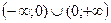
Во всех точках определения функция непрерывна
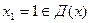
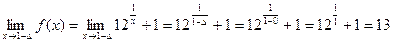
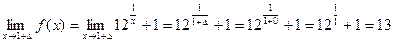
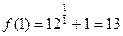
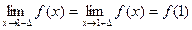
В точке x1 = 1 функция непрерывна
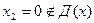
определим характер точки разрыва
Для этого найдем односторонние пределы
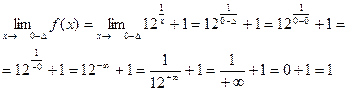
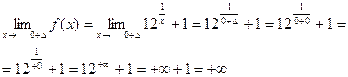
В точке x2 = 0 функция терпит разрыв второго рода
 |
 | |||||
 | |||||
 |

Пример 1.10.
Найти точки разрыва функции и определить характер разрыва. Построить график функции.
f(x)= 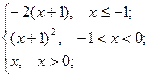
Данная функция задана тремя элементарными функциями, определенными на различных интервалах изменения х.
Функция непрерывна на каждом интервале
Разрыв возможен только в точках x1 = -1, x2 =0, где меняется аналитическое выражение функции
Для этого найдем односторонние пределы
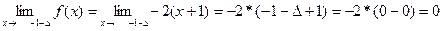
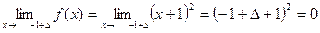
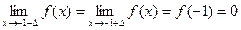
В точке x1 = -1 функция непрерывна
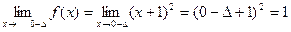
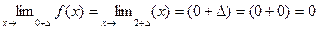
f(0)не определено
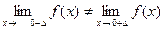
 В точке x2 = 0 функция терпит разрыв первого рода (односторонние пределы конечные числа не равные между собой)
В точке x2 = 0 функция терпит разрыв первого рода (односторонние пределы конечные числа не равные между собой)
 |
Тема 2: «Дифференциальное исчисление функции одной переменной»
Пример 2.1. Найти производную 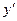
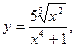 При вычислении производной данной функции следует использовать правило дифференцирования частного:
При вычислении производной данной функции следует использовать правило дифференцирования частного: 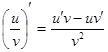 . В результате получим
. В результате получим
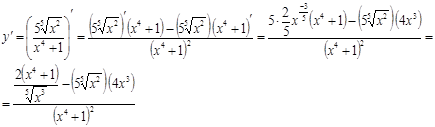
Пример 2.2. Найти производную 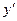
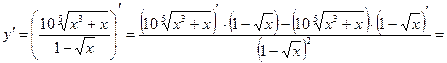
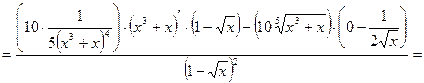
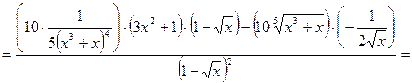
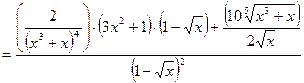
Пример 2.3. Найти производную 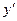
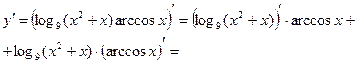
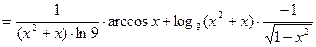
Пример 2.4. Найти производную 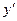
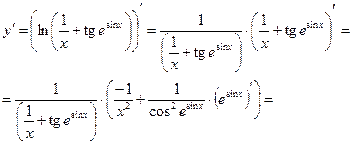
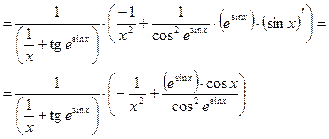
Пример 2.5. Найти производную 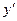
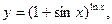
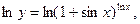
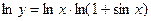
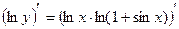
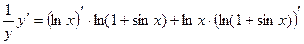
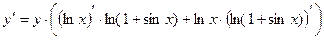
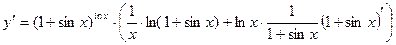
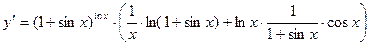
Пример 2.6. Найти производную 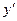
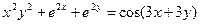
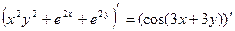
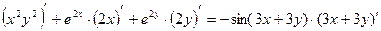
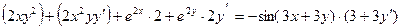
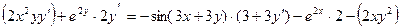
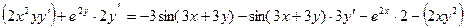
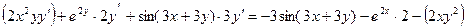
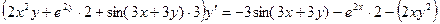
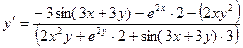
Пример 2.7. Найти производную 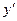
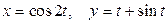 .
.
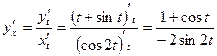
Пример 2.8.
Найти наибольшее и наименьшее значения функции y = x3–3x+1 на отрезке [1/2; 2].
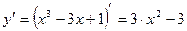
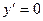
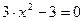
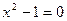
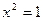
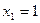
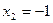
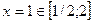
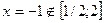
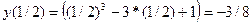
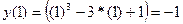
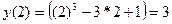
Ответ : 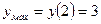
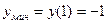
Пример 2.9.
Составьте уравнение касательной в точке 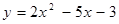
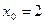
Решение:
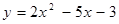
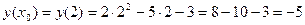
Найдем производную:
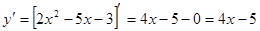 .
.
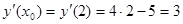
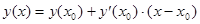 касательная
касательная
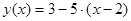
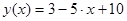
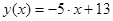
Ответ : 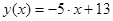 касательная к графику функции в точке
касательная к графику функции в точке
Пример 2.10. Исследовать методами дифференциального исчисления функцию.
Построить график этой функции, используя результаты исследования.
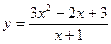
Общая схема исследования:
1. Область определения
2. Точки пересечения с осями координат
С ось ох =>у=0
3. Четность-нечетность, периодичность.
4. Точки экстремума, промежутки возрастания, убывания функции.
5. Точки перегиба, промежутки выпуклости, вогнутости.
6. Асимптоты вертикальные и наклонные.
7. График.
2) Область определения 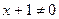
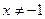 Д(х)=
Д(х)= 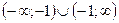
3) Точки пересечения с осями координат
С ось ох =>у=0
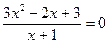
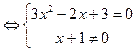
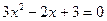
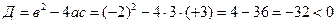
Нет точек пересечения с осями координат
3) Четность-нечетность, периодичность
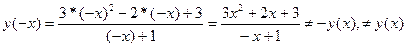 не является четной и не является нечетной, график не симметричен относительно оси оу и начала координат.
не является четной и не является нечетной, график не симметричен относительно оси оу и начала координат.
Функция не содержит тригонометрических выражений - не является периодической.
4)Точки экстремума, промежутки возрастания, убывания.
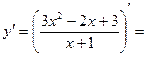
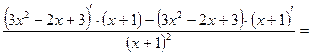
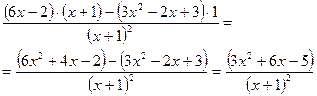
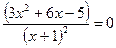
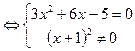
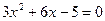
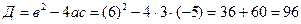
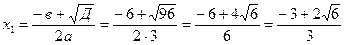
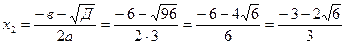
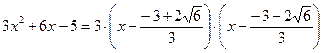
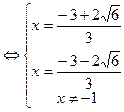 точки экстремума х=
точки экстремума х= 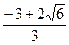 и х=
и х= 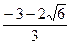
Найдем знак первой производной на промежутках области определения
| х | 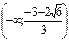 | 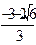 | 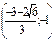 | 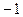 | 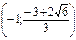 | 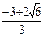 | 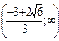 |
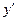 | + | - | Не опр | - | + | ||
| у |  | макс |  | Не опр |  | мин |  |
5)Точки перегиба, промежутки выпуклости, вогнутости
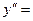
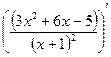 =
= 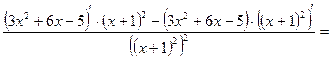
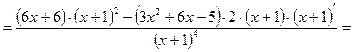
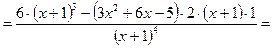
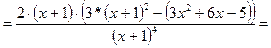
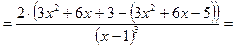
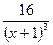
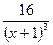
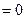
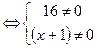 действительных корней нет, точек перегиба нет . Найдем знак второй производной на промежутках области определения.
действительных корней нет, точек перегиба нет . Найдем знак второй производной на промежутках области определения.
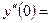
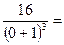
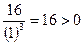
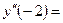
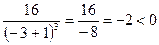
| х | 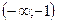 | -1 | 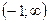 |
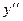 | - | Не опр | + |
| у |  | Не опр | 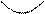 |
6) Асимптоты
У=кх+в
К= 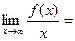
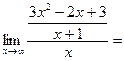
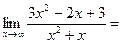
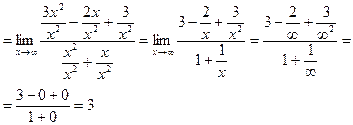
в= 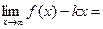
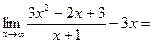
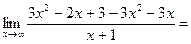
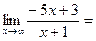
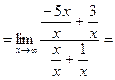
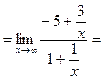
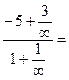
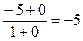
У=3х-5–наклонная асимптота
Вертикальные асимптоты
Х=1 точка разрыва
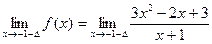 =
= 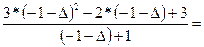 =
= 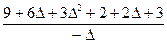 =
= 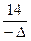 =
= 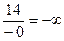
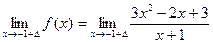 =
= 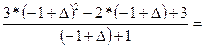 =
= 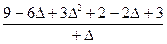 =
= 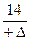 =
= 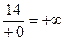

Пример 2.11.
Вычислить предельную выручку, если известны уравнения спроса10q+p-100=0 и значения цены р=80 на продукцию (- количество продукции. р-цена продукции) Что она показывает?
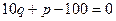
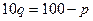
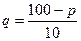
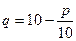
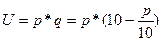
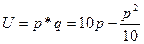
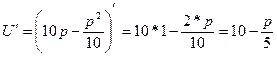
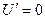
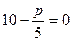
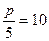
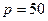 оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
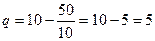 Количество товара, которое можно продать с учетом спроса при оптимальной цене.
Количество товара, которое можно продать с учетом спроса при оптимальной цене.
Пример 2.12.
Функции спроса и предложения имеют вид 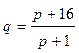 - спроса,
- спроса, 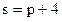 - предложения.
- предложения.
Найти: 1) равновесную цену 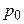 ;
;
2) эластичность спроса и предложения для этой цены 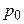 .
.
1) равновесная цена 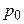 находится в случае, если спрос равен предложению
находится в случае, если спрос равен предложению
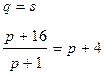
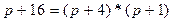
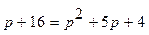
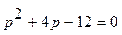
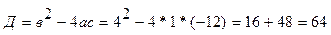
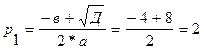
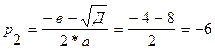
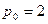 оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
оптимальная цена, при которой получаем максимальную выручку и при которой спрос равен передложению
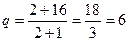 Количество товара, которое можно продать с учетом спроса при оптимальной цене.
Количество товара, которое можно продать с учетом спроса при оптимальной цене.
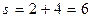 Спрос на товар по оптимальной цене
Спрос на товар по оптимальной цене
2) эластичность спроса и предложения для этой цены 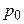 .
.
Эластичностью функции f(x) в точке x0 называют предел
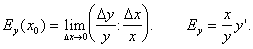
Спрос – это количество товара, востребованное покупателем. Ценовая эластичность спроса ED – это величина, характеризующая то, как спрос реагирует на изменение цены. Если |ED| > 1, то спрос называется эластичным, если |ED| < 1, то неэластичным. В случае ED = 0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.