Характеристики апериодических корреляционных функций M – последовательностей
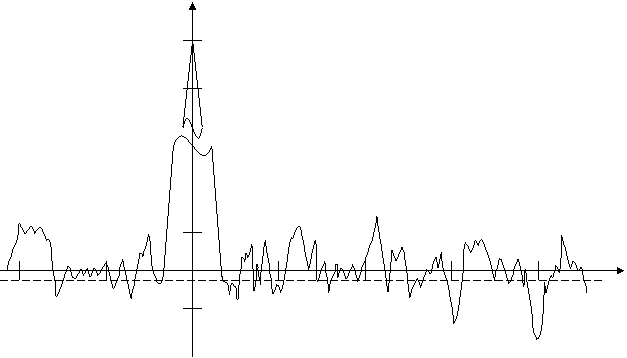
АКФ периодических М – последовательностей имеет вид, представленный на рис.2.5, где боковые пики равны - 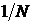 . Однако, АКФ апериодической М – последовательности рис.2.7 (N=127) имеет боковые пики существенно большие, чем у периодической ПСП.
. Однако, АКФ апериодической М – последовательности рис.2.7 (N=127) имеет боковые пики существенно большие, чем у периодической ПСП.
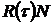
127
120 N=127
10 - 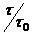
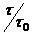
0
- 60 - 30 30 60 90 120
-10
Рис.2.7. АКФ апериодической М – последовательности с N=127.
В табл. 2.5 приведены для сравнения обобщенные характеристики КФ М – последовательностей в апериодическом режиме и СП (см. раздел 2.3), где:
-среднеквадратическое значение боковых пиков 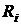 определено дисперсией
определено дисперсией
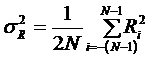 ; (2.38)
; (2.38)
-среднее значение модулей боковых пиков
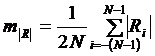 ; (2.39)
; (2.39)
-среднеквадратическое значение модулей пиков определено дисперсией
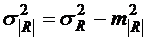 ; (2.40)
; (2.40)
-максимальные значения бокового пика 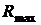 .
.
Таблица 2.5
| Корреляционные функции | 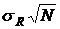 | 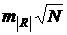 | 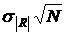 | 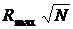 |
| АКФ М – последовательностей | 0,4 | 0,32 | 0,26 | 0,7…1,25 |
| ВКФ М – последовательностей | 0,73 | 0,54 | 0,48 | 1,4…5 |
| КФ (АКФ и ВКФ) случайных последовательностей | 0,7 | 0,56 | 0,43 | 2,1…3,5 |
Цифры, приведенные в таблице, не нормированы, т.е. умножены на 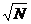 и определяют превышение σR ,
и определяют превышение σR , 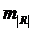 ,
, 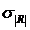 и
и 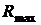 уровня
уровня 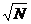 .
.
Отметим, что среднее значение боковых пиков равно 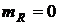 (сравни с (2.22)для СП), а ВКФ М – последовательностей имеют большие боковые пики, чем АКФ. Однако, характеристики этих ВКФ близки к статистическим характеристикам КФ СП:
(сравни с (2.22)для СП), а ВКФ М – последовательностей имеют большие боковые пики, чем АКФ. Однако, характеристики этих ВКФ близки к статистическим характеристикам КФ СП: 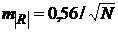 ,
, 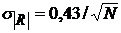 , что и обусловило их название “псевдослучайные последовательности”.
, что и обусловило их название “псевдослучайные последовательности”.
Следует отметить также, что уровень 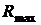 для различных М – последовательностей может превышать значение 1/
для различных М – последовательностей может превышать значение 1/ 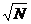 в 5…6 раз.
в 5…6 раз.
2.4.2. Многофазные сигналы. Амплитудно-фазоманипулированные
Сигналы
Максимальные уровни боковых пиков 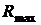 апериодических АКФ ПСП конечной длительности можно уменьшить, применяя многофазные сигналы и амплитудно-фазоманипулированные сигналы.
апериодических АКФ ПСП конечной длительности можно уменьшить, применяя многофазные сигналы и амплитудно-фазоманипулированные сигналы.
Многофазные сигналы можно построить дискретизацией аналоговых сигналов с ЧМ, например, линейно-частотной модуляцией (ЛЧМ). На рис.2.8, изображена зависимость фазы θ от t огибающей сигнала с ЛЧМ (рис.1.1) в форме записи (1.15).
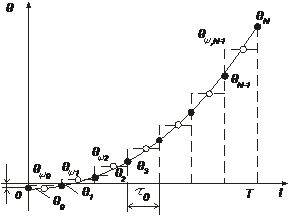
Рис.2.8. Зависимость фазы θ огибающей сигнала с ЛЧМ
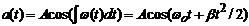 , где
, где 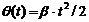 .
.
ЛЧМ сигнал длительностью Т можно представить в виде последовательности N радиоимпульсов с мгновенной частотой, линейно изменяющейся в течение импульса 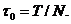 Значения линейно-ломанной аппроксимирующей дискретной функции совпадают с непрерывной θ(t) в точках, кратных τ0, т.е. θn=θ (n τ0), n = 0,1,…N-1.
Значения линейно-ломанной аппроксимирующей дискретной функции совпадают с непрерывной θ(t) в точках, кратных τ0, т.е. θn=θ (n τ0), n = 0,1,…N-1.
Если в качестве начальных фаз многофазного сигнала ЧМ взять
θфn=(θn+θn+1)/2, то начальные фазы n-го импульса многофазного сигнала, соответствующего аналоговому сигналу ЛЧМ, равны:
θфn=(n2+n) π/N. (2.41)
Меняя β (т.е. θфn ) получим систему многофазных сигналов.
Модуль АКФ такого многофазного сигнала равен
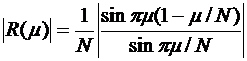 . (2.42)
. (2.42)
В качестве аналогового сигнала можно взять также сигнал с квадратичной частотой модуляцией (КЧМ). Известно, что модули АКФ этих аналоговых и соответствующих многофазных сигналов близки, а боковые пики 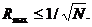
Амплитудно-фазоманипулированные (АФМ) сигналы. Можно показать [1], на основании (2.8), что идеальной АКФ ФМ ПСП без боковых пиков соответствует бесконечная ПСП. Реальные конечные ПСП, уменьшающие боковые пики АКФ ПСП символов an, n=0,1…N, можно построить, уменьшая амплитуды крайних оставленных и отброшенных символов бесконечной ПСП, отсчитываемых от середины ПСП. При этом известно, что лучшим АФМ сигналом является ПСП символов рис.2.9а с квадратичным фазовым спектром Ψ(ω) (2.7) КП и огибающей (1.13) с косинусной формой, т. е. пик - фактором 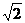 .
.
Если произвести двоичное квантование (клипирование) по уровню АФМ сигнала (рис.2.9а), т.е. получить 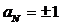 (рис.2.9б), то получим ФМ сигнал, АКФ которого будет обладать большими, но все же достаточно малыми боковыми пиками.
(рис.2.9б), то получим ФМ сигнал, АКФ которого будет обладать большими, но все же достаточно малыми боковыми пиками.
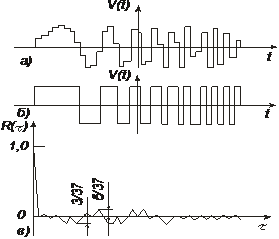
Рис.2.9. АФМ сигнал (а), ФМ сигнал (б), АКФ ФМ сигнала (в).
Например, АФМ сигнал с квадратичным фазовым спектром при N=37 имеет максимальный боковой пик АКФ 1,5%. При этом максимальный боковой пик АКФ ФМ сигнала (рис.2.9в) равен 5/37=0.135, что несколько меньше 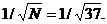 Можно показать, что среднеквадратичное значение боковых пиков АКФ таких ФМ сигналов (при оптимальном выборе их параметров) равно
Можно показать, что среднеквадратичное значение боковых пиков АКФ таких ФМ сигналов (при оптимальном выборе их параметров) равно 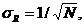 т.е. такие сигналы можно отнести к оптимальным (или минимаксным) ФМ сигналам.
т.е. такие сигналы можно отнести к оптимальным (или минимаксным) ФМ сигналам.
Минимаксными ФМ сигналами называют сигналы, у которых максимальные боковые пики АКФ минимальны.
2.4.3.Cистемы ФМ сигналов
Ранее отмечалось, что для помехозащищенных ШСС требуется большой объем L (1.5) нормальных и больших систем ФМ ШПС.
К такому объему можно приблизиться, реализуя системы сигналов на основе, например, систем Уолша или производные системы [1] ФМ сигналов на основе М-последовательностей.
Система сигналов Уолша. Многие системы ФМ сигналов образованы на базе систем сигналов Уолша, построенных на основе матрицы Адамара
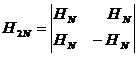 , (2.43)
, (2.43)
где HN - матрица Адамара порядка N, а H2N - порядка 2N.
Полагая H1=1 из (2.43) можно получить матрицы порядка 2
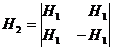 или 4,8…2т, где т-целое число. Например, порядка 8
или 4,8…2т, где т-целое число. Например, порядка 8
 (2.43')
(2.43')
В качестве КП системы Уолша можно брать строки или столбцы матрицы Адамара. Число этих КП (объём системы) равно порядку матрицы N.
Обозначим j-ю кодовую последовательность Уолша в (2.43') как {Wj}, 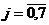 , а её п-ый символ через Wj(п). На основании уравнения ортогональности матриц Адамара
, а её п-ый символ через Wj(п). На основании уравнения ортогональности матриц Адамара 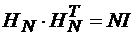 , где в обычном произведении матриц Т - знак транспонирования, а I- единичная матрица, можно записать уравнение ортогональности ПСП Уолша
, где в обычном произведении матриц Т - знак транспонирования, а I- единичная матрица, можно записать уравнение ортогональности ПСП Уолша
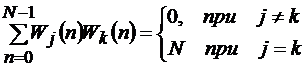 . (2.44)
. (2.44)
На рис.2.10 приведены ПСП системы Уолша согласно матрице Н8, которые упорядочены по числу блоков μ в последовательности.
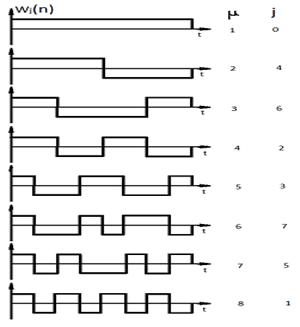
Рис.2.10. Система сигналов Уолша.
Отметим, что число блоков μ в различных последовательностях изменяется от 1 до N, 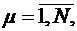 и плохо согласуется с блоковой структурой кода СП (2.23), (2.27). Поэтому система сигналов Уолша обладает плохими корреляционными свойствами, т.е. АКФ и ВКФ имеют большие боковые пики.
и плохо согласуется с блоковой структурой кода СП (2.23), (2.27). Поэтому система сигналов Уолша обладает плохими корреляционными свойствами, т.е. АКФ и ВКФ имеют большие боковые пики.
При этом спектр (2.6) кодовой ПСП Уолша с μ=1 имеет максимум (рис.2.1) при ω = 0, а с μ = N имеет максимум при ω = π/τ0 и оба максимума равны N. Соответственно максимум СПМ равен N2. У остальных ПСП максимумы лежат между ω = 0 и ω = π/τ0.
На базе систем Уолша можно строить производные системы сигналов.
Производным сигналом называют сигнал, образованный посимвольным произведением двух или более исходного и производящего сигналов, которые могут быть узкополосными и широкополосными.
К таким системам можно отнести:
-сегментные cистемы, реализуемые путем выделения перекрывающихся или не перекрывающихся сегментов (отрезков) из ПСП на основе М-последовательности большой длины N;
-циклические системы Голда, Касами.
Выбор производящего сигнала зависит от исходного сигнала. Если исходный сигнал U широкополосный, то производящий V тоже широкополосный с малыми уровнями боковых пиков ФН. Если исходный сигнал узкополосный, то для производящего сигнала достаточно многократное превышение полосы исходного сигнала и малый уровень боковых пиков АКФ.
Производные сегментные системы сигналов. Обозначим комплексную огибающую (1.15) исходной М-последовательности U(t), где
0 ≤ t ≤T, а модуль огибающей (1.13) производящего сигнала V(t)=1, 0 ≤ t ≤ T0, гдеT0 < T. В этом случае выделение сегмента из ПСП эквивалентно применению узкополосного производящего сигнала с прямоугольной огибающей и длительностью, равной длительности сегмента T0.
Производный сигнал
Sp(t)=U(t+tp)∙V(t) (2.45)
называют р-м сегментом, расположенным на отрезке [0,T0], который вырезается из исходного сигнала (ПСП) на отрезке [tp, tp+T0]. Последовательность сегментов 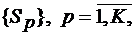 образует систему сигналов
образует систему сигналов
с объемом системы при примыкающих сегментах 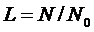 и длительностью сегмента
и длительностью сегмента 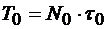 .
.
ВКФ сегментов и максимальные боковые пики ВКФ сегментов равны:
:
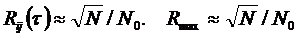 . (2.46)
. (2.46)
При проектировании системы сигналов задается эффективное значение ВКФ 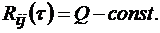 При заданном Q и известном, например, N ПСП из (2.46) определяют длительность сегмента
При заданном Q и известном, например, N ПСП из (2.46) определяют длительность сегмента 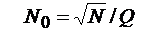 и объем системы
и объем системы 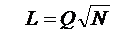 .
.
Производный сигнал может формироваться и при перекрывающихся сегментах.
Производные циклическиесистемысигналов. Пусть для циклических систем даны две кодовые ПСП {А(ν)}, {В(ν)}, где ν- номер символа в ПСП, 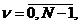 а символы А(ν), В(ν) принадлежат мультипликативной комплексно-сопряженной р-ичной группе.
а символы А(ν), В(ν) принадлежат мультипликативной комплексно-сопряженной р-ичной группе.
Если р >2, то будем называть сигнал многофазным. Этим ПСП можно поставить в однозначное соответствие цифровые кодовые ПСП {а(ν)}, {b(ν)},символы которых а(ν), b(ν) принадлежат аддитивным р-ичным группам.
При р =2 символами ПСП {А(ν)}, {В(ν)} являются 1 и -1, а символами цифровых ПСП являются 0 и 1.
Формирование КФ (2.18) сводится к перемножению символов А(ν) и В*(ν) с последующим суммированием, где *-знак комплексной сопряженности.
При переходе к символам а(ν), b(ν) КФ определяется через разности этих символов по mod p на основе сравнения (Примечание стр.23)
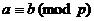 , т.е.
, т.е. 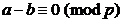 . (2.47)
. (2.47)
Для циклических систем ФМ сигналов ПСП {а(ν)}, {b(ν)} должны обладать следующим циклическим свойством: разность по mod p ПСП {а(ν)} и её циклической перестановкой {а(ν+μ)} является другой циклической перестановкой {а(ν+λ)} исходной ПСП, т.е.
{а(ν)} - {а(ν+μ)}= {а(ν+λ)}, (2.48)
где λ≠0 и λ≠μ(mod p). Аналогично:
{ b(ν)}- {b(ν+μ)}= {b(ν+λ)}.
Равенства (2.48) выполняются для М-последовательностей согласно их аддитивно-циклическим свойствам.
Пример. Циклические перестановки получаются так: исходная ПСП {а(ν)} записывается в виде периодической бесконечной ПСП:
…a(N-2),a(N-1), a(0), a(1),…a(ν),… a(μ),… a(N-2), a(N-1), a(0), a(1),a(μ), ..
Т.е. она начинается с символа a(0) и заканчивается символом a(N-1) . Циклическая перестановка {а(ν+μ)} начинается с символа a(μ) при ν=0 и заканчивается при ν = N-1символом a(μ +N-1).
Циклическая система сигналов состоит из последовательностей {Сj(ν)}, 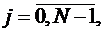 символы которых определяются равенством
символы которых определяются равенством
Cj(ν)=a(ν)-b(ν+j), (2.49)
где 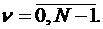
Каждая ПСП циклической системы равна разности между ПСП {а(ν)} и ПСП циклической перестановки {b(ν+j)}, т.е.
{Cj(ν)}={a(ν)-b(ν+j)} (2.50)
Такие циклические системы являются производными, где система последовательностей {b(ν+j)} является исходной, а ПСП
{а(ν)}- производящей.
Известно, что ВКФ сигналов циклической системы определяются периодическими ВКФ, ВФН образующих последовательностей. Поэтому для построения циклической системы минимаксных сигналов (Rmax→min) необходимо, чтобы периодические ВКФ и ВФН образующих сигналов имели малые боковые пики (Rmax(λ)→min). Общего метода построений таких сигналов нет.
Циклические системы Голда. По методу Голда образующим двоичным (p=2) М-последовательностям длины N=2n-1 должны соответствовать примитивные многочлены, корнями которых являются α-ν для первой и (α2l+1)-ν для второй последовательностей, где l -любое целое число, взаимно-простое с п.
Примитивным называют неприводимый (не может быть представлен в виде произведения) многочлен, одним из корней которого является примитивный элемент поля Галуа GF(2n).
Корень α называется примитивным, если все его степени (α0, α1 ,..αN= α0) дают различные элементы поля.
Такие образующие ПСП выбираются по известным [1] таблицам неприводимых многочленов и периодические нормированные ВКФ ПСП циклической системы сигналов являются случайными уровнями с
максимальными боковыми пиками
Rmax (λ ) ≤ 1,4/ 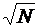 , (2.51)
, (2.51)
что меньше в 2 раза, чем для полного кода (3/ 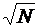 ).
).
Пример. Полагая обозначения n=k эквивалентными, возьмем [2] в качестве образующих М-последовательностей пару при k=5 предпочтительных ПСП длины N=2k-1=31, которым соответствуют полиномы 101001 и 111011(см. раздел 2.4.1):
f1(x) =а0x5+а3x2+1
f2(x) = а0x5+а1x4+ а3x2+ а4x+1. (2.50')
Эти ПСП имеют трехуровневую периодическую ВКФ {-1, -t(k), t(k) -2}, где уровень t(k) определен (2.32').
Из этой пары ПСП {a(ν)} и {b(ν)} образуем согласно (2.50) ансамбль
последовательностей {Cj(ν)}, 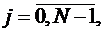 длины N каждая, взяв для каждого циклического сдвига j посимвольную сумму по mod2 символов последовательности {a(ν)} и символов циклически сдвинутой на j версии ПСП {b(ν+j)} или наоборот. Таким образом, получим N новых периодических последовательностей с периодом N=2k-1.
длины N каждая, взяв для каждого циклического сдвига j посимвольную сумму по mod2 символов последовательности {a(ν)} и символов циклически сдвинутой на j версии ПСП {b(ν+j)} или наоборот. Таким образом, получим N новых периодических последовательностей с периодом N=2k-1.
Если включить в этот ансамбль и исходные ПСП {a(ν)} и {b(ν)}, то получим ансамбль из (N+2)=33 ПСП. Эти ПСП называют последовательностями Голда, из которых 31 ПСП не являются последовательностями максимальной длины. Схема реализации генератора предпочтительных М-последовательностей, которым соответствуют примитивные многочлены (2.50'), и генератора ПСП Голда представлена на рис.2.10'.
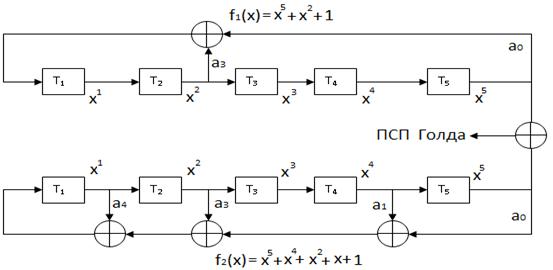
Рис.2.10'. Схема реализации генератора предпочтительных
М-последовательностей (2.50') и соответсвующих ПСП Голда
АКФ ансамбля из 31 ПСП Голда не являются в отличие от М-последо-вательностей двоичными. Голд показал, что значения ВКФ любой пары ПСП ансамбля (N+2) последовательностей Голда и пиковые значения не нормированной АКФ Rmax являются троичными с возможными значениями {-1,-t(k), tk-2}, где уровень t(k) определен (2.32').
Циклические последовательности Касами образуются аналогичными процедурами согласно (2.50), где, если ввести задержку D(j), то можно записать в виде:
{Cj(ν)}={А(ν)} 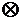 {D(j)B(ν)}, (2.52)
{D(j)B(ν)}, (2.52)
где символ 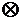 - посимвольное умножение последовательностей {А(ν)} и {D(j)B(ν)}, а произведение D(j)B(ν) является символом B(ν), сдвинутым на jтактов. Число всех ПСП равно N+2 (N сдвигов плюс две исходных ПСП).
- посимвольное умножение последовательностей {А(ν)} и {D(j)B(ν)}, а произведение D(j)B(ν) является символом B(ν), сдвинутым на jтактов. Число всех ПСП равно N+2 (N сдвигов плюс две исходных ПСП).
Для малой системы Касами с ансамблем 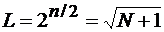
предложено брать исходные М - последовательности: {А(ν)} с периодом 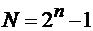 , а { B(ν)} с периодом
, а { B(ν)} с периодом 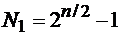 и
и 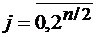 .
.
Пример. Рассмотрим процедуру генерации [2] ансамбля ПСП Касами из L=2k/2 двоичных ПСП периода N=2k-1, когда k–четно.
В этой процедуре начинаем с М-последовательности {a} и формируем двоичную последовательность {b}, взяв каждый (2k/2+1) символ из {a}, т.е. последовательность {b} формируется путем децимации (прореживания) {a} через (2k/2+1) символ. Полученная последовательность {b} периодическая с периодом (2k/2-1), например, при k =10 период ПСП {a} равен N=2k-1=1023, а период {b} равен (2k-1)=31. Следовательно, если мы будем наблюдать 1023 символа последовательности {b}, то увидим 33 повторения 31 символьных последовательностей.
Теперь, взяв N=2k-1 символа из ПСП {a} и {b}, мы формируем новый ансамбль ПСП путем суммирования по mod2 символов из {a} и символов {b} и всех (2k/2-2)=30 циклических сдвигов символов из {b}.
Включая ПСП {a} в ансамбль, мы получим ансамбль объемом из L=2k/2 (1 ПСП {a}+1 ПСП{b}+30 ПСП{b} циклической перестановки) двоичных ПСП длины N=2k-1 каждая, которые называются последовательностями Касами.
АКФ и ВКФ (не нормированные) этих ПСП имеют значения из ряда: {-1,-(2k/2 +1), 2k/2 -1}, а максимальное значение ВКФ для любой пары ПСП этого ансамбля равно 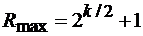 . Эта величина удовлетворяет нижней границе
. Эта величина удовлетворяет нижней границе 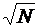 , найденной Уолшем для любой пары двоичных ПСП периода N=2k-1 в ансамбле М - последовательностей. Следовательно, малые ПСП Касами длины N=2k-1 из ансамбля L=2k/2 оптимальны.
, найденной Уолшем для любой пары двоичных ПСП периода N=2k-1 в ансамбле М - последовательностей. Следовательно, малые ПСП Касами длины N=2k-1 из ансамбля L=2k/2 оптимальны.
Большая система Касами получается при произвольном перемножении двух исходных М–последовательностей с периодом 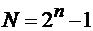 , образующих циклическую систему (2.52), на М–последовательность с периодом
, образующих циклическую систему (2.52), на М–последовательность с периодом 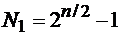 , где п - четно. Символически этот алгоритм можно записать в виде:
, где п - четно. Символически этот алгоритм можно записать в виде:
{Kij(ν)}={А(ν)} 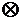 {D(j)B(ν)}
{D(j)B(ν)} 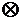 {D(i)∙ C(ν)}, (2.53)
{D(i)∙ C(ν)}, (2.53)
где {А(ν)}, {B(ν)} - ПСП периода N, а {С(ν)} - ПСП периода N1; D(j), D(i) – символы сдвига, 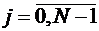 ,
, 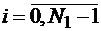 .
.
При значении степени характеристического полинома исходных ПСП 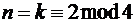 объем большой системы Кассами:
объем большой системы Кассами: 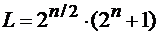 ,
,
а при 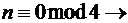 соответственно
соответственно 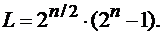
При больших п объем большой системы Касами 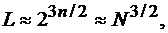 т.е. в
т.е. в 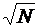 раз больше объема нормальной системы. Максимальные пики нормированной ВКФ малой и больших систем Касами удовлетворяют соотношению
раз больше объема нормальной системы. Максимальные пики нормированной ВКФ малой и больших систем Касами удовлетворяют соотношению 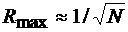 , которое в 2 раза превышает эффективную оценку (2.14), полученную из условия ограниченности объема тела ВФН и в
, которое в 2 раза превышает эффективную оценку (2.14), полученную из условия ограниченности объема тела ВФН и в 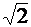 раз эффективную оценку (2.22)
раз эффективную оценку (2.22) 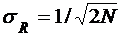 для СП.
для СП.
Большие производно-циклические системы можно построить на посимвольном перемножении производящей последовательности {V} на последовательность Уолша {Wm} и на циклическую последовательность Голда {Gn} или вместо системы Голда можно использовать большую систему Касами {Kn} (2.53). В этом случае j-я ПСП определяется следующим образом:
{Aj}={V} 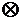 {Wm}
{Wm} 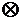 {Gn}
{Gn}
{Aj}={V}  {Wm}
{Wm}  {Kn}. (2.54)
{Kn}. (2.54)
Поскольку 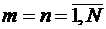 , то
, то 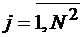 , т.е. объем системы сигналов для первой системы равен
, т.е. объем системы сигналов для первой системы равен 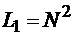 . Так как объем системы {Kn} равен
. Так как объем системы {Kn} равен 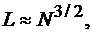 то
то 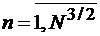 и объем второй системы равен
и объем второй системы равен 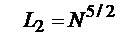 . Однако характеристики ВКФ этих систем (2.54) неизвестны.
. Однако характеристики ВКФ этих систем (2.54) неизвестны.
Известно, что среднее значение объема больших систем сигналов определяется нижней границей, которая, при допустимом уровне R0<<1 (максимума модуля нормированной ВКФ), равна:
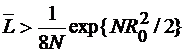 (2.55)
(2.55)
т.е. растет экспоненциально от 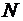 .
.
Однако, реальная оценка объема больших систем сигналов равна
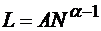 , (2.56)
, (2.56)
где A-const, зависящая от N и α,; α-const, зависящая от N и допустимого уровня R0, например: для L=N → α=2;адляL=N2 → α=3 и т. д.
Кроме того, для лучших больших систем ФМ сигналов известны верхняя и нижняя оценки максимальных пиков нормированных КФ 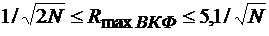 (2.57)
(2.57)
Таким образом, циклические системы Голда и Кассами позволяют строить нормальные и большие системы ФМ сигналов.
Однако, линейные рекуррентные ПСП (М-последовательности, последовательности Голда, Кассами) не обеспечивают помехозащищенность (структурную скрытность) систем связи с ШПС.
Известно [2,5,6], что постановщику помех достаточно произвести посимвольный прием 2∙k символов М-последовательности, следующих друг за другом, чтобы раскрыть закон её формирования и перехватить
информацию или сформировать имитирующую помеху подавления ШСС.
