Тема. понятие соответствия

Содержание

1.Понятие соответствия между множествами

2.Способы задания соответствий

3.Соответствие обратное данному. Взаимно однозначное соответствие

4.Равномощные множества. Счетные множества

Основная литература [ ];

Дополнительная литература [ ]

ПРАКТИЧЕСКАЯ РАБОТА. СООТВЕТСТВИЯ МЕЖДУ ДВУМЯ МНОЖЕСТВАМИ (С/Р)

Цель. Показать практическую значимость при изучении математики в начальной школе понятий соответствия, способов задания соответствий; познакомится с новыми понятиями: соответствие, обратное данному, взаимно однозначное соответствие, равномощные множества, счетное множество.

Теоретическая часть

Вопросы к изучению

1. Понятие соответствия между множествами

2. Способы задания соответствий

3. Соответствие обратное данному. Взаимно однозначное соответствие

4. Равномощные множества. Счетные множества

Основные понятия темы

Ø соответствие, обратное данному;

Ø взаимно однозначное соответствие;

Ø равномощные множества;

Ø счетное множество.

Определения, замечания, выводы

Ø Любое соответствие S между множествами Х и Y есть подмножество декартова произведения этих множеств, т.е. S Ì Х ´ Y.

Ø Задают соответствия так же, как и множества вообще.

Ø Графики взаимно обратных соответствий между числовыми множествами симметричны относительно биссектрисы 1 – го и 3 – го координатных углов.

Практическая часть

Обязательные задания

1. Вычислив длины заданных отрезков, учащийся записал: АВ = 7см, СD = 12 см, KL = 15cм, XY= 12см. Соответствие между какими множествами он установил? Задайте это соответствие при помощи предложения с двумя переменными и графа.

2. Даны множества: Х = {2,5}, Y = {3,6}. Перечислите элементы декартова произведения данных множеств и образуйте все подмножества полученного множества. Какое из подмножеств задает соответствие: а) «больше»; б) «меньше»; в) «меньше на 1»; г) «меньше в 3 раза»?

3. Соответствие «число х в два раза больше числа у» рассматривается между множествами Х и Y . Каким будет его график, если: а) Х = {2,4,6,8}, Y = N; б) Х = [2,8], Y = R; в) Х = Y = R.

4. Множества Х = {1,3,4,6} и Y = {0,1} находятся в соответствии S = {(1,1), (3,0), (3,1), (4,0), (4,1), (6,1)}. Задайте соответствие S^-1, обратное соответствию S, и постройте на одном чертеже их графики.

5. Между множествам Х – углов треугольника АВС и множеством Y – его сторон задано соответствие Т – «угол х лежит против стороны у». Задайте соответствие Т^-1, обратное соответствию Т, при помощи: а) предложения с двумя переменными; б) графа.

6. Задайте при помощи графа соответствия между множествами Х = {а, б, с} и Y = {2, 4, 6} так, чтобы одно из них было взаимно однозначным.

7. Даны множества: А= {1,2,5}, В = {3,7}. Найдите А´B и В´А. Верно ли, что найденные множества равномощны?

8. Докажите, что множество А счетно, если: а) А = {9, 10, 11, 12,…}; б) А = {а êа = 3п, п ÎN}; в) А = {а êа = п², п ÎN}.

10. Покажите, что выполняя нижеприведенные задания, учащиеся начальных классов используют понятие равночисленности множеств:

а) Нарисуй на другой фигуре столько же точек, сколько на первой (точки не пересчитывать).

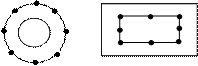
б) Нарисуй, не считая, столько же квадратов и столько же отрезков, сколько на рисунке треугольников.

в) У Димы было 28 марок, а у Коли на 7 марок больше. Сколько марок было у Коли?

г) У Маши 9 игрушек, а у Риты на 2 меньше. Сколько игрушек у Риты?

д) Для детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили детям?

е) Для детского сада купили 15 красных мячей, а зеленых в 3 раза меньше. Сколько зеленых мячей купили детям?

Творческие задания

1. Сколько взаиМно однозначных соответствий можно установить между двумя множествами. Состоящими из двух элементов? Из трех элементов?

2. Установите взаимно однозначное соответствие между множеством N и множеством N \ R; где Р – множество натуральных чисел от 1 до п.

3. Является ли множество всех целых чисел счетным?

ПРИМЕРНЫЙ ВАРИАНТ КОНТРОЛЬНОЙ (ЗАЧЕТНОЙ) РАБОТЫ

Группа А

1. Выбери правильный из ответов:

а) множество – это набор объектов определенной природы;

б) под множеством понимают совокупность объектов, отвечающих определенным свойствам;

в) под множеством понимают совокупность элементов, которые можно пересчитать.

2. Среди следующих высказываний укажите истинные: а) 100 Î N; б) -8 Î Z; в) 5,36 Î Q; г) 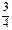Î N; д) 0 Î Z; е) -3ÏN; ж) 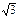Î Q; з)102ÏR; и) 1,3Î N.

3. Х – множество прямых плоскости. Какое из следующих отношений является отношением эквивалентности на этом множестве: а) «х параллельна у»; б) «х перпендикулярна у»; в) «х пересекает у»?

Группа Б

1. Найдите АÈB, АÇB, А \ В, если: А = { х | хÎR, -5< х< 5}, В = { х | хÎR, 1£ х < 4}.

2. Из множества К = {0, 2, 6, 8, 9, 12, 15}выделили два подмножества: К₁ - числа, кратные 2; К₂ -числа, кратные 3. Произошло ли разбиение множества К на классы? Почему?

3. На множестве Х={0, 3, 6, 9, 12, 15, 18} задано отношение R.Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R –« х больше у в 3 раза»; б) R – « х больше у на 3».

Группа В

1. Даны два множества А ={4, 6, 8} и В ={3, 7}. Найдите множества А ´B и B´A. Можно ли установить взаимно однозначное соответствие между ними?

2. Проверьте справедливость равенства (A \ B)´С=(A´С) \ (B´С)для множеств А = {3, 5, 7}, В = {5, 7}, С = {1, 4}.

3. На множестве Х = { 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} задано отношение «иметь один и тот же остаток от деления на 4». Показать, что данное отношение есть отношение эквивалентности, записать все классы эквивалентности, на которые разбивается множество Х, построить граф этого отношения.

Критерии оценки:Задания группы А оцениваются 1 баллом, группы Б – 2 баллами, группы В – 3 баллами. Выполнение заданий группы А обязательно; за каждое не правильно выполненное задание этой группы от общего количества баллов вычитают 1 балл. За 7-10 баллов студент получает оценку «3» (зачет), за 11-14 – оценку «4», за 15 – 18 – оценку «5».