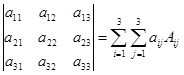Операция умножения двух матриц водится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы
Произведением матрицы Amxn =(ail) на матрицу Bnxp=(blk) называется матрица Cmxp=(Cik) такая, что 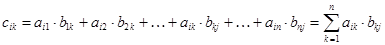
Таким образом, каждый элемент 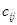 , находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Если матрицы А и В квадратные, одного размера, то произведения А×В и В×А всегда определены. Причем А×Е=Е×А=А, где А- квадратная матрица, Е- единичная матрица того же размера.
Матрицы называются перестановочными, если А×В=В×А.
Умножение матриц обладает следующими свойствами:
1. А ×(В × С)=(А × В) × С 2. А ×(В+С)=А × В+А × С
3. (А+В) × С=А × С+В × С 4. a ×(А × В)=(a × А) × В
Если эти суммы и произведения имеют смысл.
Для операции транспонирования матриц верны следующие свойства: (А+В)Т=АТ+ВТ; (А × В)Т=ВТ × АТ.
Определители. Основные понятия
Если матрица квадратная, то ее можно оценить (определить), то есть поставить в соответствие число.
Определение. Определителем D матрицы А (или detА) называется многочлен, составленный из элементов этой матрицы. Для матрицы порядка n, определитель записывается в виде:
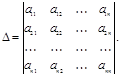
Если матрица числовая, то значение определителя есть число, которое находят по известным правилам.
Свойства определителей:
1. Определитель матрицы не изменится, если матрицу протранспонировать: 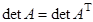 .
.
2. Определитель матрицы равен нулю, если он содержит строку (столбец), все элементы которой равны нулю.
3. Определитель матрицы равен нулю, если элементы двух строк (столбцов) одинаковые.
4. Определитель матрицы равен нулю, если элементы двух строк (столбцов) пропорциональны.
5. Определитель матрицы меняет свой знак на противоположный, если поменять места две строки (столбца).
6. Если все элементы некоторой строки (столбца) имеют общим множитель, то он выносится за знак определителя.
7. Если к одной строке (столбцу) определителя прибавить другую строку (столбец), умноженную на число, то значение определителя не изменится.
8. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
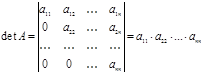
Вычисление определителей
Определитель 2-го порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали, то есть 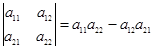
Определитель 3-го порядка вычисляется по формуле:
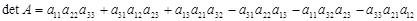
Для ее запоминания используется мнемоническое правило - правило треугольников. Оно состоит в изображении (явном или мысленном) элементов матрицы точками. Точки, соответствующие произведениям, которые входят в определитель, соединяются отрезками.

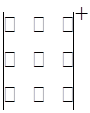

Главной диагонали и двум треугольникам, основания которых параллельны главной диагонали, соответствуют произведения со знаком «+», а побочной диагонали и треугольникам, основания которых ей параллельны, соответствуют произведения со знаком «-».
Определение. Минором к порядка, 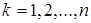 , матрицы порядка n называется определитель, полученный из исходного вычеркиванием n-k строк и n-k столбцов. Определитель, составленный из элементов стоящих на пересечении вычеркнутых n-k строк и столбцов, называется дополнительным минором к минору k порядка.
, матрицы порядка n называется определитель, полученный из исходного вычеркиванием n-k строк и n-k столбцов. Определитель, составленный из элементов стоящих на пересечении вычеркнутых n-k строк и столбцов, называется дополнительным минором к минору k порядка.
Определение. Минором 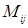 элемента
элемента 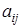 ,
, 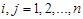 , называется определитель порядка n-1, полученный вычеркиванием строки i и столбца j из определителя D порядка n. Элемент
, называется определитель порядка n-1, полученный вычеркиванием строки i и столбца j из определителя D порядка n. Элемент 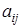 и его минор
и его минор 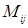 являются взаимнодополнительными минорами.
являются взаимнодополнительными минорами.
Определение. Алгебраическим дополнением элемента 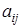 определителя D называется число
определителя D называется число 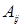 равное минору
равное минору 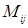 со знаком «+», если сумма i+j четная, и со знаком «-», если сумма i+j нечетная, то есть
со знаком «+», если сумма i+j четная, и со знаком «-», если сумма i+j нечетная, то есть 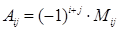 . (1)
. (1)
Определитель n-го порядка можно вычислить разложением по строке i (столбцу j). Например, для определителя 3-го порядка получаются следующие равенства:
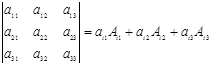 ,
, 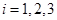 или
или