Лекция 6. Исследование систем линейных уравнений

Теорема Кронекера-Капелли. Решение систем линейных уравнений методом Гаусса

Пусть задана система из т линейных уравнений с п неизвестными :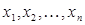

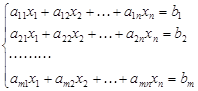
Решением системы называется такой набор чисел 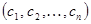, что при его подстановке в систему вместо соответствующих неизвестных (с₁ вместо х₁, …, с_п вместо х_п) каждое из уравнений системы обращается в тождество.

Если система имеет хотя бы одно решение, она называется совместной; система, не имеющая ни одного решения, называется несовместной. Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех решений этих систем совпадают.

Матрица 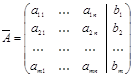называется расширенной матрицей системы.

Теорема (Кронекера-Капелли)Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы: .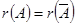

Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы – выяснить, определенна она или нет. При этом возможны три варианта:

1. Если 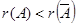, то система несовместна.

2. Если 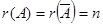, где п- число неизвестных, то система совместна и определенна.

3. Если 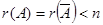, то система совместна и неопределенна.

Метод Гаусса основан на алгоритме последовательного исключения неизвестных.

Задача состоит в том, чтобы привести ее к «треугольному» виду при помощи эквивалентных преобразований, то есть получить единицы на главной диагонали и нули под ними.

Выпишем расширенную матрицу коэффициентов системы.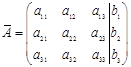

Алгоритм состоит в том, что на каждом шаге выполняются следующие действия (количество шагов определяется количеством уравнений). Выбирается одна из ненулевых, не рассмотренных ранее строк, ее номер считаем равным i. Все элементы этой строки делятся на элемент, стоящий на i-м месте (номер столбца этого элемента равен j). Если на i-м шаге какая-то из строк содержит уже на i-м месте единицу, то именно она переставляется и считается i-й строкой. Далее, добавляя к остальным строкам строку i, умноженную на подходящее число, добиваемся того, что все элементы столбца j, расположенные ниже строки i, были равны нулю.

При решении системы уравнений методом Гаусса возможны следующие случаи:

1. Если матрица 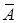приведена к треугольному виду, то система совместна и имеет единственное решение.

2. Если матрица 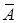содержит хотя бы одну строку, все элементы которой равны нулю, то система совместна и имеет множество решений.

3. Если матрица 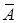содержит строку, все элементы которой, кроме свободного члена, равны нулю, то система несовместна, то есть решения не имеет.

Определение. Система линейных алгебраических уравнений (СЛУ) называется однородной, если все свободные члены системы равны нулю.

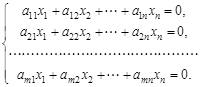
Очевидно, что однородная СЛУ всегда совместна, так как одно ее решение всегда известно: все неизвестные равны нулю.

Теорема. Однородная система имеет единственное нулевое решение, тогда и только тогда, когда определитель матрицы коэффициентов при неизвестных не равен нулю. В противном случае система имеет множество решений.