Операция сложения матриц вводится только для матриц одинаковых размеров

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. М. КОЗЫБАЕВА

РЫБАЛКО Н.А.

КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

« МАТЕМАТИКА»

Для специальности 5В072700 «Технология продовольственных продуктов»

г. Петропавловск

2014 г.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РЕСПУБЛИКИ КАЗАХСТАН

Северо-Казахстанский государственный университет

Им. М. Козыбаева

Специальность: 5В072700 «Технология продовольственных продуктов»

РЫБАЛКО Н.А.

КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

« МАТЕМАТИКА»

г. Петропавловск

2014 г.

Рецензент

Шмигирилова И. Б., к.п.н., доцент

Разработчики:

Рыбалко Н. А., старший преподаватель

Курс лекций содержит теоретический материал по всем темам курса, предусмотренным программой. Наряду с подробно излженными воросами теории содержится достаточное количество примеров.

Система менеджмента качества СКГУ им. М.Козыбаева

сертифицирована на соответствие требованиям ISO 9001:2008

Лекция 1-2. Матрицы. Определители

Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов одинаковой длины. Матрица записывается в виде:

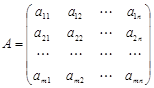(1.1)

Или сокращенно 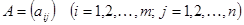где i – номер строки; j - номер столбца

Матрицу А называют матрицей размерности mxn и пишут A_mxn. Числа a_ij, составляющие матрицу, называют ее элементами.

Элементы матрицы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.

Матрицы равны между собой, еcли равны все соответствующие элементы этих матриц, т.е. А=В, если a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу nxn называют матрицей n-го порядка.

Квадратная матрица называется треугольной, если все её элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой матрицей. Обозначается буквой О и имеет вид: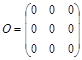

Матрица, элементы главной диагонали которой единицы, а все остальные нули, называется единичной матрицей, обозначается буквой Е и имеет вид: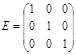

В матричном исчислении матрицы О и Е играют такую же роль, как и числа 0 и 1 в арифметике.

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^Т.

Транспонированная матрица обладает следующим свойством: (А^Т)^Т=А

Действия над матрицами.

Сложение матриц

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц А_mxn=(a_il) и B_mxn=(b_ij) называется матрица C_mxn=(c_ij) такая, что c_ij=a_ij+b_ij (i=1,2,…,m; j=1,2,…,n)

Разность матриц определяется аналогично.

Умножение матрицы на число

Произведением матрицы А_mxn=(a_il) на число k называется матрица В_mxn=(b_il) такая, что b_ij=k×a_ij (i=1,2,…,m; j=1,2,…,n)

Матрица –А=(-1)А называется матрицей противоположной матрице А.

Разность матриц А-В можно определить как А-В=А+(-В).

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

А+В=В+А 1×А=А

А+(В+С)=(А+В)+С a(А+В)=aА+aВ

А+0=А (b+a)×A=aA+bA

А-А=0 a(bA)=(ba)A

Где А, В, С – матрицы a,b- числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц называются следующие операции:

-перестановка местами двух параллельных рядов матрицы;

-умножение всех элементов ряда матрицы на число, отличное от нуля;

-прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одна из них получена из другой с помощью элементарных преобразований. Запись А~В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю.

Такую матрицу называют канонической.

Произведение матриц