Лекции 15. Элементы теории корреляции

Пусть по выборке объема п получено эмпирическое распределение:

Варианты	x1	x2	…	xm
Эмпирические (наблюдаемые) частоты	n1	n2	…	nm

По данным наблюдений выдвигают гипотезу о законе распределения генеральной совокупности, например, предполагают, что генеральная совокупность распределена равномерно или нормально. Такие гипотезы называют статистическими. Затем для тех же объектов, которые попали в выборку, вычисляют частоты, исходя уже из теоретической гипотезы. В результате получают частоты (их называют выравнивающими (теоретическими) частотами), которые, вообще говоря, отличаются от наблюдавшихся. Как определить, правильно или нет выдвинута гипотеза, т. е. случайны ли расхождения наблюдавшихся и выравнивающих частот или эти расхождения являются следствием неправильности гипотезы? Для решения этого вопроса применяют критерии согласия эмпирических наблюдений выдвинутой гипотезе. Имеется несколько критериев согласия: 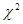(хи-квадрат) К. Пирсона, Колмогорова, Смирнова и др.

Критерии согласия и позволяют оценить вероятность того, что полученная выборка не противоречит сделанному предположению о виде закона распределения рассматриваемой случайной величины.

В различных критериях согласия в качестве меры расхождения статистического и теоретического законов распределения принимают различные величины.

В критерии согласия Пирсона (критерий χ²) за меру расхождения принимается величина χ², опытное значение 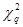которой определяется 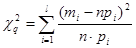, где l – число разрядов, на которые разбиты все опытные значения величины χ, n – объем выборки, m_i – численность i-го разряда, p_i – вергоятность попадания случайной величины X в интервал i-го разряда, вычисленная для теоретического закона распределения.

При 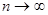закон распределения 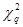независимо от вида закона распределения случайной величины стремится к закону χ²- распределения с k=l-r-1степенями свободы, где r– число параметров теоретического распределения, вычисляется по данной выборке.

Значения вероятностей 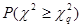в зависимости от 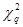и k приведены в таблице.

Для применения критерия согласия Пирсона в общем случае необходимо, чтобы объем выборки n и численность разрядов 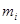были достаточно велики (практически считается достаточным, чтобы было )

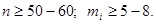Рассмотрим суть критерия 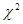Пирсона.

Предположим, что на основе приведенного выше распределения выдвинута гипотеза Н: генеральная совокупность имеет нормальное распределение. Для вычисления выравнивающих частот поступают следующим образом:

1. Находят значения ,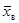

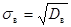
2. Выравнивающие частоты 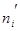ищут по формуле: 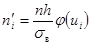, где п- сумма наблюдавшихся частот, h- разность между двумя соседними вариантами, 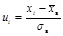и .

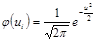В результате получено множество выравнивающих частот .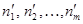

Обозначим через 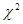сумму квадратов разностей между эмпирическими и выравнивающими частотами, деленных на соответствующие выравнивающие частоты .

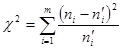Для данной выборке по этой формуле находим значение случайной величины 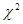. Обозначим его через 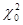. Затем определяем число 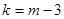, называемое числом степеней свободы, где т- число различных вариант выборки.

Теперь проверка гипотезы Н проводится следующим образом: задаемся уровнем значимости р, т. е. столь малой вероятностью р, при которой о событии 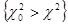, имеющем вероятность р, можно с большой уверенностью сказать, что в единичном испытании оно не произойдет. В таблице значений 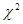по заданному уровню значимости р и числу степеней свободы к находят значение 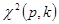. Если окажется, что 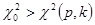, то гипотеза Н отвергается на уровне значимости р, так как произошло событие, которое не должно произойти при верной гипотезе Н; если же 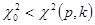, то Н принимается на уровне значимости р. Обычно в качестве р берут либо 0,05, либо 0,01, либо 0,001.

Если каждому значению одной случайной величины соответствует значение другой, то случайные величины связаны функциональной зависимостью. Однако такая строгая зависимость реализуется весьма редко, т.к. очень часто оба признака (или один из них) подвержены еще действиям случайных факторов, причем среди этих факторов могут быть и общие для обоих признаков. В этом случае и возникает другой вид зависимости – корреляционная зависимость.

Определение 1. Две случайные величины Х и Y находятся в корреляционной зависимости, если каждому значению любой из этих величин соответствует определенное распределение вероятностей другой величины.

Определение 2. Условным математическим ожиданием дискретной случайной величины Х при Y=y (у-определенное возможное значение Y) называют сумму произведений возможных значений величины Х на их условные вероятности: 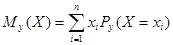, где 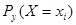- условная вероятность равенства Х=x_i при условии, что Y=y.

Для непрерывных величин 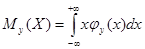, где 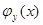- плотность вероятности случайной непрерывной величины Х при условии Y=y.

Условное математическое ожидание 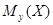есть функция от у: 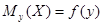, которую называют функцией регрессии величины Х на величину Y.

Корреляционная зависимость проявляется в том, что при изменении одной величины, изменяется условное математическое другой.

Аналогично определяется условное математическое ожидание случайной величины Y и функция регрессии Y на Х: .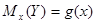

Уравнение 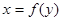( 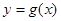) называют уравнением регрессии Х на Y (Y на Х), а линию на плоскости, соответствующую этому уравнению, называют линией регрессии.

Линия регрессии Y на Х (Х на Y) показывает, как в среднем зависит Y от Х (Х от Y).

Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции.

Определение 1. Если Х и Y- независимые случайные величины, то .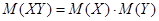

Если же Х и Y не являются независимыми случайными величинами, то .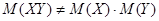

За меру связи (зависимости) двух случайных величин Х и Y приминают безразмерную величину r, определяемую соотношением: 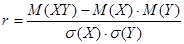или более кратко соотношением: 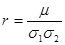, где 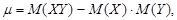, 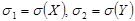и называемую коэффициентом корреляции.

При этом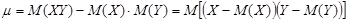

Определение 2. Случайные величины Х и Y называют некоррелированными, если r=0, и коррелированными, если .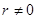

Свойства коэффициента корреляции:

1. Если Х и Y- независимые случайные величины, то коэффициент корреляции равен нулю.

2. Коэффициент корреляции по абсолютной величине не превышает единицы, т.е. 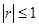, причем, чем ближе 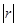к единице, тем больше корреляционная зависимость между 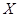и 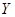приближается к линейной, а при 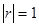случайные величины связаны линейной функциональной зависимостью.

3. Коэффициент корреляции характеризует относительную величину отклонения математического ожидания произведения 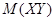от произведения математических ожиданий 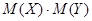величин Х и Y. Так как это отклонение имеет место только для зависимых величин, то коэффициент корреляции характеризует тесноту зависимости между Х и Y.

Определение. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регресси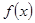и и 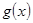являются линейными. В этом случае обе линии регрессии являются прямыми; они называются прямыми регрессиями.

Выведем уравнение прямой линии регрессии Y на Х, т. е. найдем коэффициент линейной функции .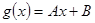

Обозначим 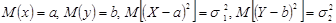. Используя свойства математического ожидания, найдем:

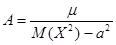или .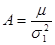

Полученный коэффициент называют коэффициентом регрессии Y на Х и обозначают :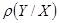

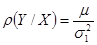
Таким образом, уравнение прямой регрессии Y на Х имеет вид 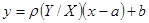. Аналогично можно получить уравнение прямой регрессии Х на Y: 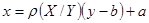, где коэффициент регрессии Х на Y: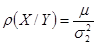

Уравнения прямых регрессии можно записать в более симметричном виде, если воспользоваться коэффициентом корреляции: 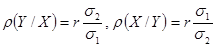и поэтому уравнения прямых регрессий принимают вид: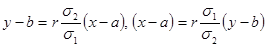

Из уравнений прямых регрессии видно, что обе эти прямые проходят через точку 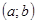; угловые коэффициенты прямых регрессии равны соответственно: .

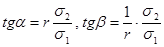Так как 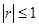, то 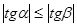. Это означает, что прямая регрессия Y на Х имеет меньший наклон к оси абсцисс, чем прямая Х на Y. Чем ближе 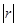к 1, тем меньше угол между прямыми регрессии. Эти прямые сливаются тогда и только тогда, когда .

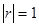При 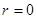прямые регрессии имеют уравнения 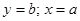. В этом случае ; .

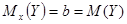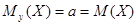Коэффициенты регрессии имеют тот же знак, что и коэффициент корреляции r, и связаны соотношением: 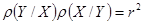.