Лекция 26. Интегрирование дробно-рациональных функций
Выделение правильной рациональной дроби
Неправильную дробь всегда можно свести к правильной, разделив числитель на знаменатель «столбиком» и выделив из дроби целую часть, т.е. многочлен: 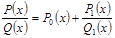
Поэтому 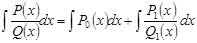 .
.
Интеграл 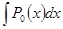 вычисляется элементарно. Рассмотрим интегрирование правильных рациональных дробей.
вычисляется элементарно. Рассмотрим интегрирование правильных рациональных дробей.
Правильные дроби следующих четырех типов называются простейшими дробями: I. 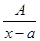 ; II.
; II. 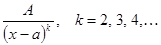 III.
III. 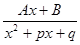 IV.
IV. 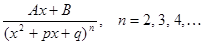
При этом предполагается, что А, В, p,q- действительные числа, а квадратный трехчлен 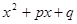 в дробях III и IV типов не имеет действительных корней (т. е.
в дробях III и IV типов не имеет действительных корней (т. е. 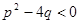 ).
).
Интегрирование простейших рациональных дробей
Рассмотри интегралы от простейших дробей:
I. 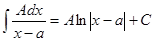 II.
II. 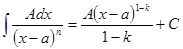
III. Для вычисления интеграла от рациональной дроби третьего типа 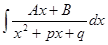 поступают следующим образом: выделяют полный квадрат в знаменателе
поступают следующим образом: выделяют полный квадрат в знаменателе 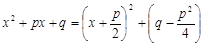 , затем делают подстановку
, затем делают подстановку 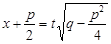 .
.
IV. Для вычисления интеграла от рациональной дроби четвертого типа, сначала, как и для дроби III типа, в числителе дроби выделяется полный квадрат, и делается подстановка
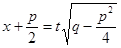 , после чего данный интеграл сводится к виду:
, после чего данный интеграл сводится к виду:
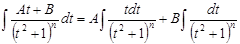 . Первый интеграл правой части легко сводится к «табличному», а второй – находится с помощью рекуррентной формулы:
. Первый интеграл правой части легко сводится к «табличному», а второй – находится с помощью рекуррентной формулы:
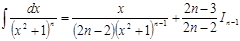 , где
, где 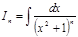
Метод неопределенных коэффициентов
Для представления правильной рациональной дроби в виде суммы простейших следует её знаменатель Q(x) разложить на множители (линейные и квадратичные с отрицательными дискриминантами) и воспользоваться следующими правилами:
1. Каждому линейному множителю (х-а) ставить в представлении f(x) слагаемое 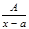 ;
;
2. Каждому множителю вида (x-a)k, k=2,3,… ставить в представлении f(x) k слагаемых 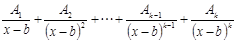 ;
;
3. Каждому множителю вида 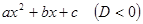 ставить в представлении f(x) слагаемое
ставить в представлении f(x) слагаемое 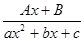 .
.
Числа А, В, А1, А2,…, Аk-1, Ak являются неопределёнными коэффициентами. Для нахождения неопределённых коэффициентов все простейшие дроби приводят к общему знаменателю Q(x) и приравнивают числители обеих частей равенства. Затем приравнивают коэффициенты при одинаковых степенях х. Это приводит к системе уравнений, из которой и находят значения интересующих нас коэффициентов.
Лекция 27. Понятие определенного интеграла
Определенный интеграл как предел интегральной суммы
Пусть функция 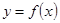 определена на отрезке
определена на отрезке 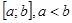 . Выполним следующие действия.
. Выполним следующие действия.
1. С помощью точек 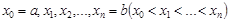 разобьем отрезок
разобьем отрезок 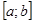 на n частичных отрезков
на n частичных отрезков 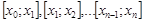 .
.
2. В каждом частичном отрезке 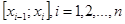 выберем произвольную точку
выберем произвольную точку 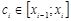 и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину 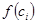 .
.
3. Умножим значение функции 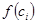 на длину
на длину 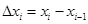 соответствующего частичного отрезка
соответствующего частичного отрезка 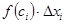 .
.
4. Составим сумму всех таких произведений: 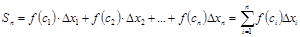 . Данная сумма называется интегральной суммой функции
. Данная сумма называется интегральной суммой функции 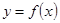 на отрезке
на отрезке 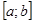 . Обозначим через
. Обозначим через 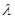 длину наибольшего частичного отрезка.
длину наибольшего частичного отрезка.
5. Найдем предел интегральной суммы, когда 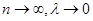 .
.
Если при этом интегральная сумма 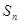 имеет предел
имеет предел 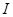 , который не зависит ни от способа разбиения отрезка
, который не зависит ни от способа разбиения отрезка 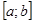 на частичные отрезки, ни от выбора точек в них, то число
на частичные отрезки, ни от выбора точек в них, то число 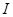 называется определенным интегралом от функции
называется определенным интегралом от функции 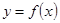 на отрезке
на отрезке 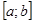 и обозначается
и обозначается 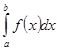 . Таким образом,
. Таким образом, 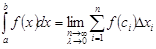 .
.
Числа 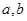 называются соответственно нижним и верхним пределами интегрирования,
называются соответственно нижним и верхним пределами интегрирования, 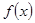 - подынтегральной функцией,
- подынтегральной функцией, 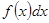 - подынтегральным выражением,
- подынтегральным выражением, 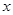 - переменной интегрирования, отрезок
- переменной интегрирования, отрезок 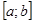 - отрезком интегрирования.
- отрезком интегрирования.
Функция 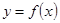 , для которой на отрезке
, для которой на отрезке 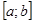 существует определенный интеграл, называется интегрируемой на этом отрезке.
существует определенный интеграл, называется интегрируемой на этом отрезке.
Фигура, ограниченная сверху графиком функции 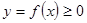 , снизу – осью ОХ, сбоку – прямыми
, снизу – осью ОХ, сбоку – прямыми 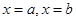 , называется криволинейной трапецией. Найдем ее площадь.
, называется криволинейной трапецией. Найдем ее площадь.
На каждом частичном отрезке построим прямоугольник, одна из сторон которого равна 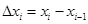 , а другая -
, а другая - 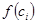 . Тогда площадь каждого такого прямоугольника равна
. Тогда площадь каждого такого прямоугольника равна 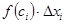 , а площадь полученной при разбиении ступенчатой фигуры -
, а площадь полученной при разбиении ступенчатой фигуры - 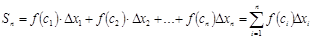 и приближенно равна площади соответствующей криволинейной трапеции.
и приближенно равна площади соответствующей криволинейной трапеции.
С уменьшением всех величин 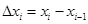 точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади криволинейной трапеции принимается предел, равный
точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади криволинейной трапеции принимается предел, равный 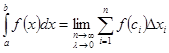 . То есть, определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
. То есть, определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
Теорема Коши:если функция 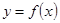 непрерывна на отрезке
непрерывна на отрезке 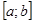 , то определенный интеграл
, то определенный интеграл 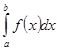 существует. (без доказательства)
существует. (без доказательства)
Укажем некоторые свойства определенного интеграла, вытекающие непосредственно из его определения:
1. Определенный интеграл не зависит от обозначения переменной интегрирования: 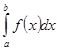 =
= 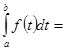
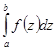 .
.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: 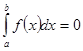 .
.
3. Для любого действительного числа с верно равенство 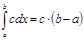 .
.
Основные свойства определенного интеграла.
1. 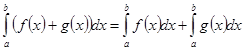 .
.
2. 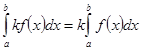 3.
3. 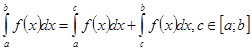
4. Если на отрезке 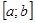 функции
функции 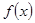 и
и 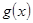 интегрируемы и
интегрируемы и 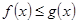 , то
, то 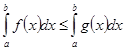 .
.
следствие 1:если 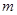 и
и 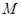 - наименьшее и наибольшее значение функции
- наименьшее и наибольшее значение функции 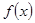 на отрезке
на отрезке 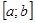 , то
, то 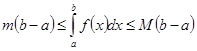 .
.
следствие 2:если на отрезке 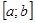 функции
функции 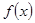 и
и 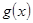 интегрируемы,
интегрируемы, 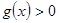 и
и 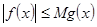 , то
, то 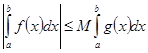 .
.
«Теорема о среднем». Если функция 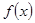 непрерывна на отрезке
непрерывна на отрезке 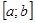 , то существует точка
, то существует точка 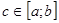 такая, что
такая, что 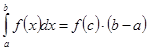 . Число
. Число 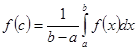 называется средним значением функции
называется средним значением функции 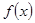 на отрезке
на отрезке 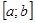 .
.
