Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Уравнения с правой частью специального вида
Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.
Различают следующие случаи:
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид: 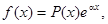 где
где
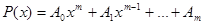 - многочлен степени m.
- многочлен степени m.
Тогда частное решение ищется в виде: 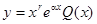
Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного диффе
II. Правая часть линейного неоднородного дифференциального уравнения имеет вид: 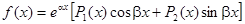
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид: 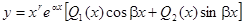 , где число r показывает сколько раз число
, где число r показывает сколько раз число 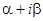 является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
Если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т.е. если уравнение имеет вид: 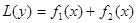 , то частное решение этого уравнения будет
, то частное решение этого уравнения будет 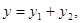 где у1 и у2 – частные решения вспомогательных уравнений
где у1 и у2 – частные решения вспомогательных уравнений
Лекция 8. Числовые ряды
Определение. Сумма членов бесконечной числовой последовательности 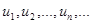 называется числовым рядом.
называется числовым рядом. 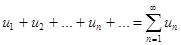 При этом числа
При этом числа 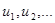 будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда.
Определение. Суммы 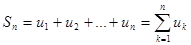 , n = 1, 2, … называются частными (частичными) суммамиряда.
, n = 1, 2, … называются частными (частичными) суммамиряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение. Ряд 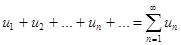 называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм. 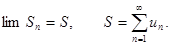
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда 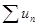 и
и 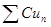 , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд 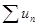 сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд 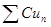 тоже сходится, и его сумма равна СS. (C ¹ 0)
тоже сходится, и его сумма равна СS. (C ¹ 0)
3) Рассмотрим два ряда 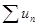 и
и 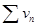 . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд 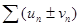 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды 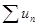 и
и 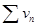 сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд 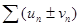 тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s. 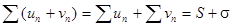
Разность двух сходящихся рядов будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Как правило используются более простые признаки сходимости:
1) Если ряд 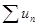 сходится, то необходимо, чтобы общий член un стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд
сходится, то необходимо, чтобы общий член un стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд 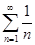 является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.
2) Если ряд сходится, то последовательность его частных сумм ограничена. Однако, этот признак также не является достаточным.
Например, ряд 1-1+1-1+1-1+ … +(-1)n+1+… расходится, т.к. расходится последовательность его частных сумм в силу того, что 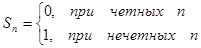
Однако, при этом последовательность частных сумм ограничена, т.к. 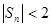 при любом n.
при любом n.
Замечание:Ряд 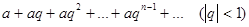 составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет
составленный из членов любой убывающей геометрической прогрессии, является сходящимся и имеет 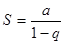
Замечание:ряд 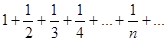 называется гармоническим, расходится.
называется гармоническим, расходится.
