Основные уравнения магнитного поля
Математической моделью стационарного магнитного поля нелинейной магнитной системы, заданного известным распределением в декартовой системе координат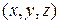 
объемных плотностей токов 
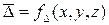, является система уравнений, в которую входят [3,4]:
- первое уравнение Максвелла
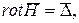(2.1)
где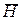 
- вектор напряженности магнитного поля,
- уравнение непрерывности магнитного поля
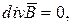(2.2)
где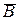 
- вектор магнитной индукции,
- уравнение связи между векторами индукции и напряженности магнитного поля (в виде характеристик намагничивания среды)
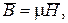(2.3)
где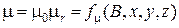 
– магнитная проницаемость в средах нелинейной магнитной системы.
Для тангенциальных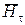 
и нормальных 
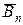составляющих на границе раздела сред 
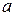и 
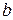уравнения граничных условий можно записать в виде:
; 
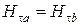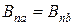. (2.4)
Для граничных условий на границе области поля нелинейной системы:
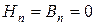, (2.5)
если за пределами области поля имеется среда с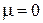 
, и
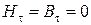, (2.6)
если за пределами области поля имеется среда с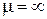 
.
Существующие аналитические методы не могут обеспечить решение системы уравнений (2.1)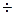 
(2.6). В магнитной системе электромеханических устройств это связано с их сложной трехмерной геометрией, многообразием границ раздела сред с различными магнитными свойствами, нелинейностью характеристик намагничивания ферромагнитных материалов. Для получения возможности аналитического решения принимается ряд упрощающих допущений:
- зубчатые поверхности магнитных сердечников заменяются гладкими;
- основное поле и поля рассеяния насыщенной машины рассматриваются независимо;
- магнитное поле насыщенной машины представляется в виде суммы двух независимых полей, по продольной и поперечной осям;
- коэффициенты поля, найденные в линейном приближении, используются при расчете насыщенной машины;
- насыщение магнитной цепи машины учитывается коэффициентом насыщения и т.д.
Разработанные на основе этих допущений упрощенные математические модели ЭМП имеют невысокую точность и их применение ограничивается предварительными проектными расчетами.
С ростом электромагнитных нагрузок применение указанных допущений приводит к заметным ошибкам на стадии проектирования ЭМП. Возможность повышения степени достоверности математических моделей ЭМП, прежде всего, связана с глубоким анализом магнитного поля в ферромагнитных средах на основе применения современных численных методов решения нелинейных краевых задач. Такие исследования позволяют не только по-новому построить математические модели ЭМП, но и учесть особенности электромагнитных процессов, возникающие в ЭМП с высокими электромагнитными нагрузками и нетипичными для электрических машин общепромышленного применения конфигурациями и соотношениями геометрических размеров. Современный уровень развития методов решения краевых задач математической физики и возможности вычислительной техники позволяют существенно уточнить и дополнить математические модели ЭМП. На основе распределения магнитного поля в ЭМП можно определить такие величины, как электромагнитные силы (ЭМС) и электромагнитные моменты (ЭММ) и т.д.