Пример выполнения задания. Задача. Парашютист спрыгивает с высоты h0 и раскрывает парашют на высоте h1

Задача. Парашютист спрыгивает с высоты h₀ и раскрывает парашют на высоте h₁. Определить, будет ли скорость приземления безопасной.

Цель моделирования. Определить конечную скорость движения тела и сравнить ее с безопасной (10 м/с).

Формализация. Будем считать, что форма человека близка к сферической, форма парашюта – полусферической. Тело характеризуется массой m, радиусом (r- человека и r₁ – парашюта) и площадью поперечного сечения ( S и S₁ соответственно). Среда характеризуется плотностью ρ и вязкостью μ. В ходе движения меняются время t, скорость v и высота h. Задача состоит в том, чтобы определить v_кон в момент времени, когда h станет близкой к нулю.

Построение математической модели. Воспользуемся моделью (2):

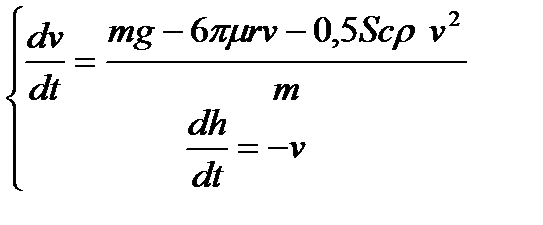
Выбор метода исследования. Применим для решения системы дифференциальных уравнений метод Эйлера:

; ;

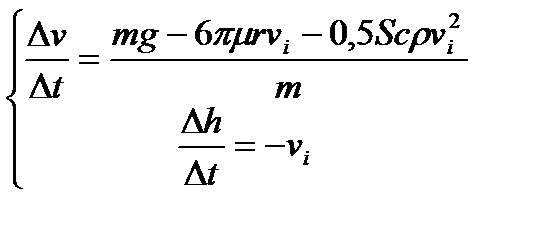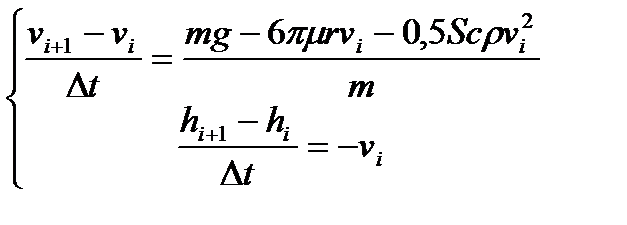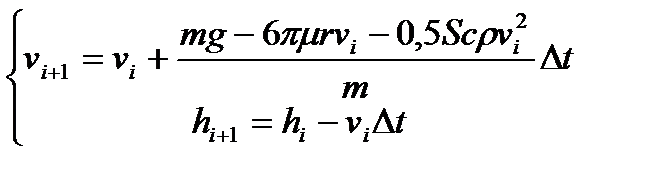
Построение компьютерной модели и ее проверка Выберем для моделирования среду табличного процессора Excel. Для проверки модели на адекватность рассмотрим движение без сопротивления среды (k₁=0 и k₂=0)

Свободное падение тела
Параметры движения	Параметры тела	Параметры среды	Коэффициенты
Время t0		Масса m		Вязкость	0,0182	k1	0,000
Скорость v0		Радиус r	0,3	Плотность	1,2	k2	0,000
Высота h0		Радиус r1	1,5
Высота h1		Площадь S	0,053
Шаг ∆t	0,5	Площадь S1	7,069
		Коэффициент с	0,40
		Коэффициент с1	0,55

Рис. 2 Исходные данные задачи о свободном падении (сопротивление среды не учитывается)

Изменение скорости и высоты со временем

t	v	h
0,5	4,9	1000,0
	9,8	997,6
1,5	14,7	992,7
	19,6	985,3
2,5	24,5	975,5
	29,4	963,3
3,5	34,3	948,6
	39,2	931,4
4,5	44,1	911,8
	49,0	889,8
5,5	53,9	865,3
	58,8	838,3
t	v	h
6,5	63,7	808,9
	68,6	777,1
7,5	73,5	742,8
	78,4	706,0
8,5	83,3	666,8
	88,2	625,2
9,5	93,1	581,1
	98,0	534,5
10,5	102,9	485,5
	107,8	434,1
11,5	112,7	380,2
	117,6	323,8
12,5	122,5	265,0

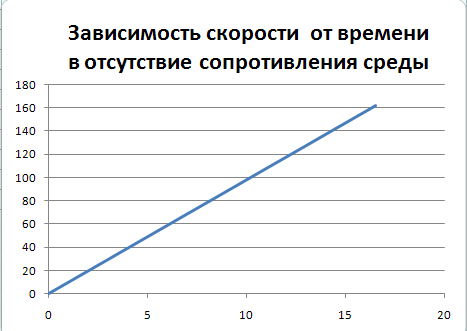
В отсутствие сопротивления среды скорость растет со временем по линейному закону, что соответствует аналитическому решению уравнений

Добавим силу сопротивления ( 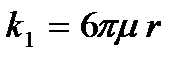и )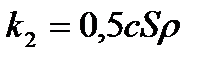

Свободное падение тела с учетом сопротивления
Параметры движения	Параметры тела	Параметры среды	Коэффициенты (без парашюта)
Время t0		Масса m		Вязкость	0,0182	k1	0,045
Скорость v0		Радиус r	0,3	Плотность	1,2	k2	0,013
Высота h0		Радиус r1	1,5			Коэффициенты (с парашютом)
Высота h1		Площадь S	0,053			k1	0,515
Шаг ∆t	0,5	Площадь S1	7,069			k2	2,333
		Коэффициент с	0,40
		Коэффициент с1	0,55

Изменение скорости и высоты со временем

t	v	h
0,5	4,9	1000,0
	9,8	997,6
1,5	14,7	992,7
	19,6	985,3
2,5	24,4	975,5
	29,3	963,3
3,5	34,1	948,7
	38,9	931,6
4,5	43,7	912,2
	48,4	890,3
5,5	53,1	866,1
	57,8	839,6
6,5	62,4	810,7
	10,3	779,5
7,5	13,7	774,3
	15,8	767,5

t	v	h
8,5	17,0	759,6
	17,6	751,1
9,5	17,9	742,3
	18,1	733,3
10,5	18,2	724,3
	18,2	715,2
11,5	18,2	706,1
	18,2	697,0
12,5	18,2	687,9
	18,2	678,8
13,5	18,2	669,7
	18,2	660,6
14,5	18,2	651,5
	18,2	642,3
15,5	18,2	633,2
	18,2	624,1
16,5	18,2	615,0

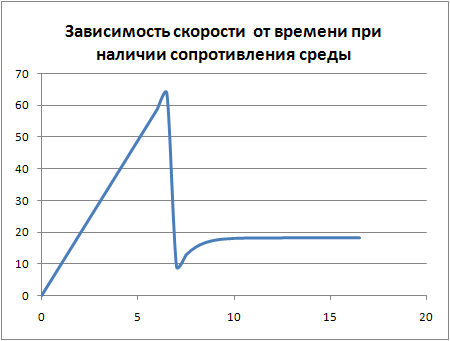Вывод. Если при падении с высоты 1000 м раскрыть парашют на высоте 800 метров,
то скорость падения 18,2 м/с значительно превысит безопасную

Использование модели

Данная модель позволяет решать не только описательные, но и оптимизационные задачи, например:

- Найти оптимальную с точки зрения безопасности высоту раскрытия парашюта;

- Найти оптимальные размеры парашюта;

- Найти максимальную высоту, с которой можно спрыгнуть без парашюта и не пострадать и т.д.