V. Продолжение работы по теме урока. 1. В ы п о л н е н и е задания № 370

1. В ы п о л н е н и е задания № 370.

– Рассмотрите рисунок. Как изображен муравей слева? (В натуральную величину.)

– Как он изображен справа? (В увеличенном виде.)

– Определите масштаб увеличенного изображения и запишите его.
(Масштаб 10 : 1.)

– Объясните, как вы рассуждали. (Надо измерить размеры муравья слева и справа с помощью линейки. Затем выполнить деление 50 : 5 =
= 10 : 1.)

– Что означает масштаб 100 : 1? В каком случае применяется такой масштаб? (При увеличении реальных размеров.)

– Начертите прямоугольник со сторонами 2 мм и 4 мм. Удобный получился чертеж?

– Что надо сделать, чтобы чертеж стал удобным? Какой надо использовать масштаб? Объясните свой выбор. (Масштаб 10 : 1.)

– Начертите данный прямоугольник в масштабе 10 : 1. Чему будут равны его стороны на чертеже? (2 см и 4 см.)

2. В ы п о л н е н и е задания № 388.

– Прочитайте условие задачи.

– Что известно в задаче? Что требуется узнать?

– Выполните чертеж к задаче и решите ее.

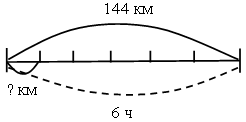
Р е ш е н и е:

144 : 6 = 24 (км в час) – скорость теплохода.

– Как надо вычислить скорость движения?

– Чтобы определить скорость движения, надо пройденный путь разделить на время движения.

– Составьте обратную задачу, в которой нужно определить путь, пройденный теплоходом. (Теплоход двигался 6 часов со скоростью 24 км в час. Какой путь прошел теплоход?)

– Придумайте несколько ситуаций, где используется путь.

3. Р а б о т а в печатной тетради № 3, задание № 37.

Р е ш е н и е. Восстановить единичный отрезок можно на первом, втором и последнем лучах сверху вниз. Третий луч дан неверно, так как расстояние между точками 0 и 3 меньше утроенного расстояния между точками 3 и 4.

VI. Итог урока.

– Что нового узнали на уроке?

– Как выбрать единичный отрезок на числовом луче, если координаты точек соответствуют дробным числам?

– Как узнать скорость движения?

– Какие задачи называют обратными?

Домашнее задание:учебник, № 370 (4); тетрадь № 3, задание № 38.

Задание 38. При использовании таблицы лучше начать с расстановки минусов в соответствии с условиями задачи: так как ежику не досталось выражения, в котором есть действия первой ступени, минусы ставятся в первой строке в первом и третьем столбцах таблицы: так как белочка не получила выражения с действиями второй ступени, минусы нужно поставить в ее строке во все столбцы кроме первого. Отсюда следует, что белочке досталось первое выражение (ставим + в соответствующей клетке, в остальных клетках первого столбца ставим –). Находим значения остальных выражений и сравниваем с решениями данной в задании системы неравенств. Значения третьего и четвертого выражений являются ее решениями, а второго нет. Значит, это выражение досталось зайчику. В остальных клетках его строки и второго столбца ставим минусы. В третьем столбце три верхние клетки заняты минусами, значит, третье выражение досталось мышке, а четвертое – ежику.

У р о к 110 (30).
Сложное (двойное) неравенство

Цели: ввести понятие о сложном (двойном) неравенстве; учить читать, записывать и составлять сложное неравенство на основе преобразования нескольких простых; совершенствовать навыки нахождения точек с дробными координатами на числовом луче; продолжить формирование навыков решения задач, основанных на знании суммы углов треугольника; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. И г р а «Молчанка».

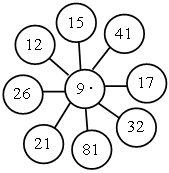
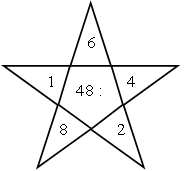
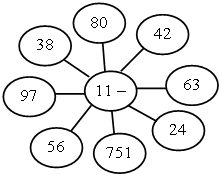
2. З а д а ч а.

В Центре детского творчества 7 кружков юных техников по 15 человек в каждом, 8 кружков рукоделия по 10 человек в каждом и 6 кружков рисования по 12 человек в каждом. Объясните, что обозначают выражения:

15 · 7 10 · 8 15 · 7 – 10 · 8 12 · 6 – 10 · 8

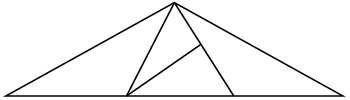
3. Сколько треугольников на чертеже?

4. Вставьте знаки >, < или =, чтобы получились верные записи:

(76 + 53) · 9 …76 · 9 + 53 · 15

7 · 4 + 3 · 4 … (7 + 3) · 4

17 · 5 … (9 + 8) · 6.