Преобразование лапласа. основные теоремы преобразования лапласа

ОСНОВНЫЕ ТЕОРЕМЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА.

Функция 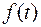называется оригиналом, если:

1) ;

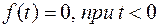2) 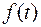- кусочно-гладкая кусочно-непрерывная функция;

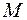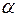3) существует показатель роста, т. е. найдутся такие числа и , что . (*)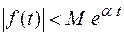

Наименьшее из чисел 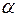или предел, к которому стремится наименьшее число, для которого справедливо равенство (*), называется абсциссой абсолютной сходимости и обозначается .

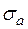В дальнейшем под изображением 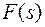будем понимать:

.

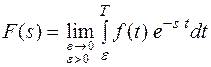Такое уточнение изображения никак не сказывается на выполнении прямого и обратного преобразования Лапласа. Оно проявляет себя лишь в некоторых свойствах преобразования Лапласа.

Теорема 1.

Если 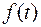является оригиналом, то изображение 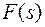определено в области 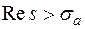и является в этой области аналитической функцией.

Первая часть теоремы, утверждающая существование изображения в области 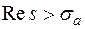, непосредственно следует из обобщенного преобразования Фурье. Докажем, что изображение 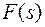в этой области является аналитической функцией.

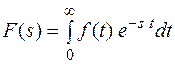
продифференцируем по s

.

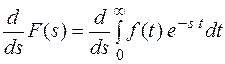Переходя к дифференцированию под знаком интеграла, получим

.

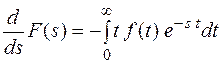Покажем, что интеграл существует. Оценим

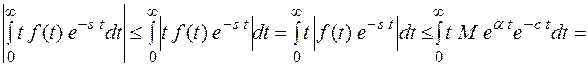
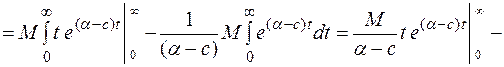
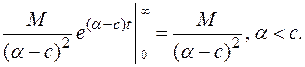
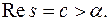
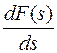Т. о. получили, что интеграл существует, следовательно, производная существует при можно взять сколь угодно близким числу . Отсюда следует, что существует в области 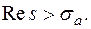Теорема доказана.

Теорема 2(основная теорема об обратном преобразовании Лапласа).

Если функция 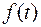является оригиналом, а 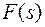- изображение функции 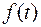, то в каждой точке t непрерывности функции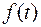

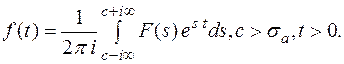
Доказательство этой теоремы следует из обобщенного преобразования Фурье. Она уточняет, что обратное преобразование Лапласа сходится к 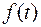только в точках непрерывности функции 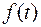. В точках разрыва 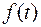обратное преобразование Лапласа сходится к среднему значению.

ЛЕКЦИЯ 12

План лекции

1. Изображение некоторых элементарных функций.

2. Линейность преобразования Фурье.

3. Теоремы об изображении производной и интеграла.

4. Теоремы об изменении масштаба, смещения в комплексной области.

ИЗОБРАЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

1.Найдем преобразование Лапласа функции 1(t): L[1(t)].

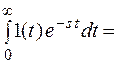
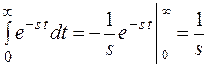
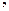
L[1(t)] = при Res > 0 ( )

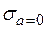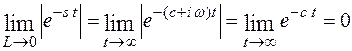, при с >0

L[1(t)] = 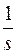, при Res > 0 .

2. Найдем преобразование Лапласа функции sinbt: L[sinbt].

L[sinbt] =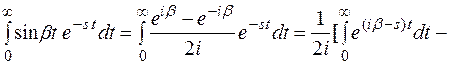

,

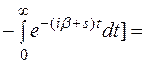
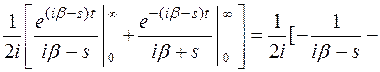
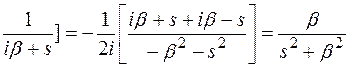
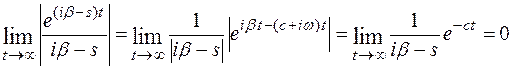при с 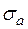> 0, > 0 .

Приведем таблицу соотношений оригинал-изображение.

№	f(t)	F(s)	sa
	1(t)	1/s
	e-α t	1/(s+α)	-α
	eα t	1/(s-α)	α
	sinbt	β/(s2+β2)
	cosbt	s/(s2+β2)
	t	1/s2
	tn	n!/sn+1

СВОЙСТВА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА.

1.Линейность преобразований.

Теорема 1.

Если функция f₁(t) и f₂(t) являются оригиналами и имеют, соответственно, изображения F₁(s) и F₂(s), то преобразование Лапласа от соотношения

L[k₁ f₁(t) 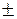k₂ f₂(t)] = k₁F₁(s) 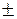k₂ F₂(s) ,

где k₁, k₂- некоторые константы.

Доказательство.