Понятие и функции комплексного переменного

СПЕЦГЛАВЫ МАТЕМАТИКИ

КОНСПЕКТ ЛЕКЦИЙ

для студентов

Направление подготовки: 550200 Автоматизация и управление

Специальности подготовки:

210500 Системы управления

летательными аппаратами

071800 Мехатроника

210300 Роботы и

робототехнические системы

120900 Проектирование

технологических комплексов

очной формы обучения

Тула 2000г.

ОГЛАВЛЕНИЕ

ЛЕКЦИЯ 1.............................................................................................................4

ЛЕКЦИЯ 2............................................................................................................10

ЛЕКЦИЯ 3............................................................................................................15

ЛЕКЦИЯ 4............................................................................................................20

ЛЕКЦИЯ 5............................................................................................................25

ЛЕКЦИЯ 6............................................................................................................29

ЛЕКЦИЯ 7............................................................................................................34

ЛЕКЦИЯ 8............................................................................................................41

ЛЕКЦИЯ 9............................................................................................................48

ЛЕКЦИЯ 10..........................................................................................................55

ЛЕКЦИЯ 11..........................................................................................................62

ЛЕКЦИЯ 12..........................................................................................................68

ЛЕКЦИЯ 13..........................................................................................................75

ЛЕКЦИЯ 14..........................................................................................................83

ЛЕКЦИЯ 15..........................................................................................................93

ЛЕКЦИЯ 16.........................................................................................................100

ЛЕКЦИЯ 17.........................................................................................................106

АННОТАЦИЯ

Излагаются математические методы, необходимые для качественного усвоения курса "Теория автоматического регулирования". Рассматриваются следующие разделы математики: элементы теории функции комплексного переменного, причем особое внимание уделяется теории вычетов; преобразование Фурье и преобразование Лапласа; разностные уравнения и решетчатые функции; дискретное преобразование Лапласа и Z-преобразование, а также свойства Z-преобразования. Вводится обобщенная функция Дирака (d-функция) и рассматривается дифференцирование разрывных функций, т.е. обобщенная производная таких функций.

Изложение сопровождается рассмотрением значительного числа примеров, которые, на наш взгляд, улучшают усвоение материала.

ЛЕКЦИЯ 1

План лекции

1. Понятие комплексного числа.

2. Комплексная плоскость. Тригонометрическая форма записи комплексных чисел.

3. Извлечение корня из комплексного числа.

4. Понятие области на комплексной плоскости.

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

1. Комплексная плоскость. Тригонометрическая форма записи комплексного числа.

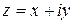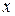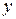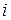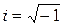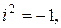
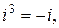
Комплексным числом называется выражение вида , где и действительные числа, - мнимая единица ( ), причем 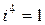и т.д.

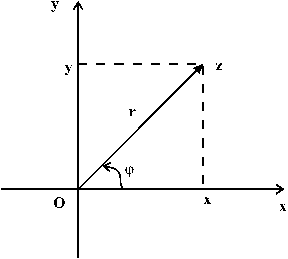Рассмотрим плоскость с прямоугольной декартовой системой координат. Такая плоскость называется комплексной. Точку на комплексной плоскости можно задать с помощью радиуса 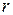и полярного угла .

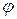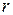- модуль комплексного числа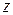 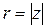, 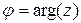; 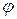- аргумент числа .

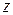За положительное направление угла 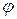принят отсчет против часовой стрелки от положительного направления оси .

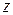Аргумент комплексного числа является неоднозначной величиной и задается с точностью до слагаемого кратного двум. В дальнейшем аргумент, как многозначную величину будем обозначать 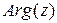, а для конкретности сохраним .

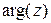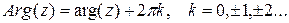
Главное значение аргумента: .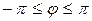

Из рисунка видно, что

;

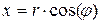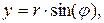
таким образом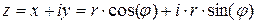

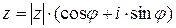- тригонометрическая форма записи комплексного числа.

;

; ; ;

;

;

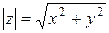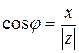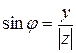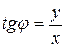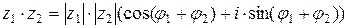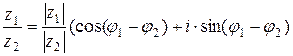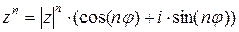- формула Муавра.

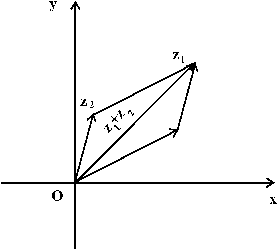
Точки на комплексной плоскости, а, следовательно, и комплексные числа можно задать с помощью вектора. При сложении и вычитании комплексных чисел используют общие правила сложения и вычитания векторов.

Извлечение корня из комплексного числа.

(*)

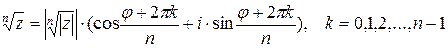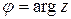
Пусть 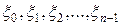- корни 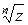. Из равенства (*) следует, что

(**)

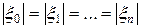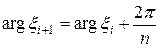
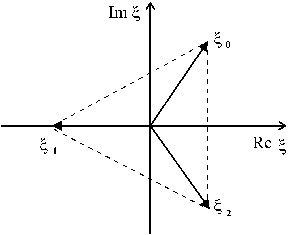
Из равенства (**) следует, что если комплексные корни изобразить на комплексной плоскости в виде вектора, то вершины этих векторов будут лежать в углах правильного 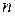-угольника, вписанного в окружность радиуса .

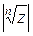Пример. Найдем корень третьей степени из числа –1.

; ;

;

;

, ;

,

, .

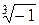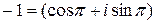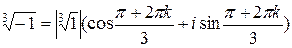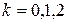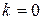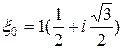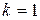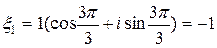
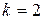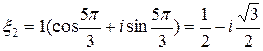ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

1.Область на комплексной плоскости.

Областью на комплексной плоскости называется множество D точек z, удовлетворяющих следующим свойствам:

1) вместе с каждой точкой z из множества D области принадлежит и некоторый круг с центром в данной точке: 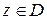(свойство открытости);

2) любые две точки можно соединить линией, состоящей из точек множества (свойство связанности).

Рис. 1

Простейшим примером области является понятие e окрестности на комплексной плоскости.

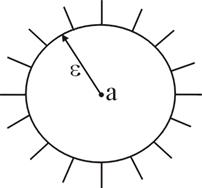Под e окрестностью точки а понимают открытый круг радиусаe с центром в точке а (рис. 2), т.е. множество точек z удовлетворяют неравенству: .

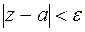Рис.2

Точка z называется граничной точкой области, если сама она области не принадлежит, но любая ее e окрестность содержит точки из области D. Совокупность граничных точек образует границу области D.

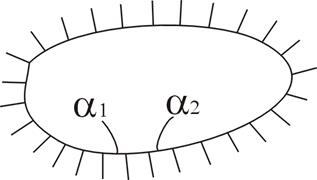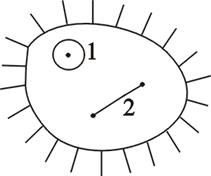
Мы будем рассматривать те области, границы которых состоят из конечного числа линий и разрезов: например на рис.3 представлена односвязная область, а на рис.4 трехсвязная область.

Рис. 3

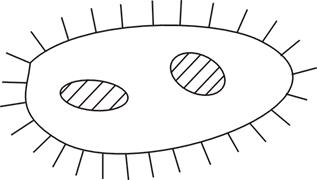Рис. 4

Число связанных частей, на которое разбивается граница области D называется порядком связанности области.

Область, присоединяющая границы, называется замкнутой областью и обозначается .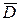

ЛЕКЦИЯ 2

План лекции

1. Функции комплексного переменного.

2. Дифференцируемость и аналитичность.

3. Условия Коши-Римана.

Понятие и функции комплексного переменного.

Рассмотрим две комплексные плоскости «W» и «z» ( ; ).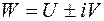

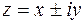Говорят, что на множестве Е плоскости «z» задана функция (W=f(z)), если указано правило, по которому каждой точке z из Е ставится в соответствие одна или несколько точек плоскости «W».

Если точка z пробегает значения множества Е, то точка W будет пробегать значения некоторого множества F.

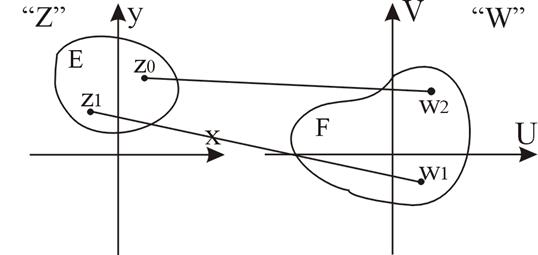Множество Е – область определения функции f(z), а множество F – область значения функции f(z).

Рис. 5

Если каждой точке z множества Е ставится в соответствие только одна точка F, то такая функция называется однозначной функцией, иначе многозначной.

Задание функции комплексного переменного эквивалентно заданию двух функций вещественного переменного.

.
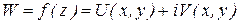