Интегрирование тригонометрических функций
Интегралы типа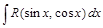 
Интегралы типа 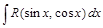, где R — рациональная функция от 
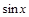и 
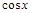, подстановкой 
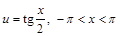можно привести к интегралам от рациональных функций.
В самом деле, если:
; 
; 
; 
; 
,
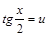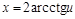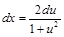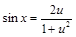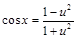тогда
= 
.
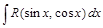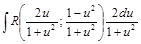Пример 1. Вычислить интеграл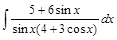 
.
Решение. Применяем универсальную подстановку
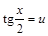, тогда ; ; ,
= 
= 
.
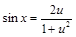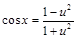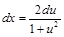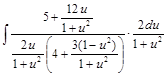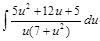Разложим дробь под интегралом на простые дроби:
.
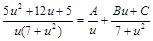Отсюда
= 
; 
; 
; 
.
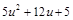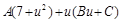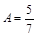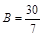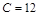Поэтому
J =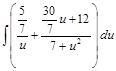 
=
= 
=
= 
.
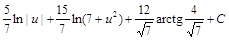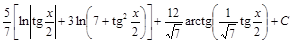Пример 2. Вычислить интеграл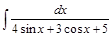 
.
Решение. Используем подстановку 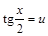, тогда
; ; .
= 
= 
=
= 
= 
= 
.
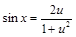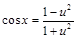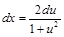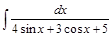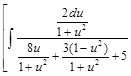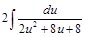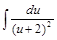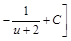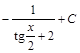Если функция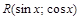 
нечетная относительно 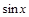или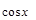 
, т.е.
= 
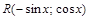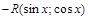
или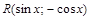 
= ,
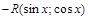то можно использовать подстановку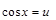 
или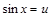 
.
Пример 3.Вычислить интеграл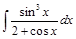 
.
Решение.
= 
= 
=
= 
= 
= 
=
= 
= 
=
= 
.
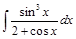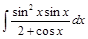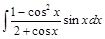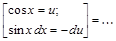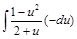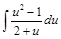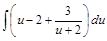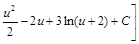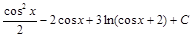Если функция четная относительно 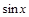и 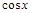одновременно, т.е.
= ,
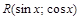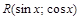то 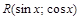можно привести к интегралу от рациональной функции с помощью подстановки 
.
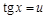Интегралы вида
; 
; 
.
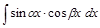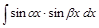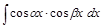Для интегрирования произведения синусов и косинусов разных аргументов применяются тригонометрические формулы:
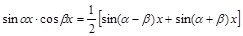
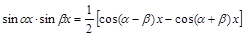
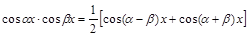
Пример 4.
=
= 
.
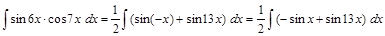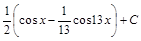Интегрирование четных степеней синусов и косинусов
.
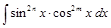Здесь следует применять формулы понижения степени
.
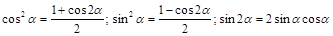Пример 5.
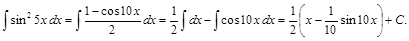
Пример 6.
= 
= 
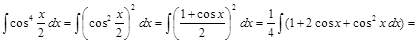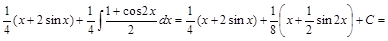
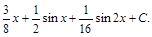
Пример 7.
.
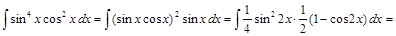
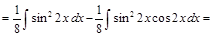
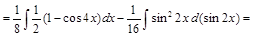
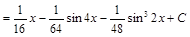Интегрирование нечетных степеней синусов и косинусов
Интегрирование
,
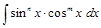где хотя бы один из показателей т и п – нечетный, (например,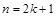 
) учитывая, что 
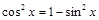, имеем:
,
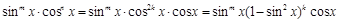где целесообразной будет подстановка .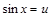
Пример 8.Вычислить интеграл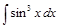 
.
Решение.
.
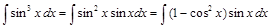Применяя подстановку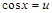 
, имеем:
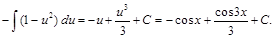
Пример 9.Вычислить интеграл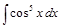 
.
Решение.
.
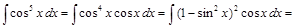
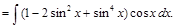Применяя подстановки
, 
,
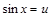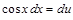имеем
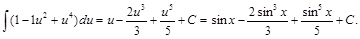
Интегрирование целых степеней тангенса и котангенса
Для интегрирования целых степеней тангенса и котангенса применяются формулы:
; 
.
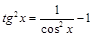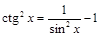Пример 10.Вычислить интеграл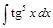 
.
Решение.
= 
= 
=
= 
= 
=
= 
= 
=
= 
.
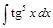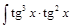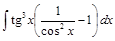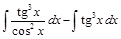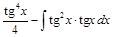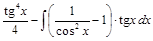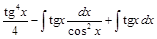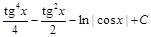Интегрирование иррациональных функций
При интегрировании выражений, которые содержат дробные степени переменной интегрирования (т.е. иррациональности), методом подстановки сводят подинтегральную функцию к рациональной дроби. Рассмотрим несколько случаев.
Интегрирование иррациональных выражений методом подстановки
Подинтегральная функция является рациональной дробью относительно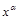 
, где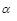 
– дробное число. В этом случае вводят новую
переменную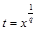 
, где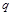 
– общий знаменатель дробных показателей степени переменной х.
Пример 1.Найти интеграл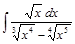 
.
Решение. Имеем: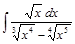 
.
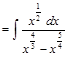Общий знаменатель дробных показателей степеней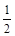 
, 
, 
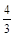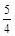переменной х равняется 12. Поэтому сделаем подстановку 
, 
, 
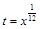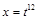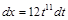и получим:
.
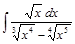
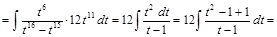
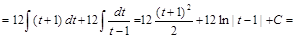
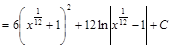Интегрирование выражений, содержащих дробные степени линейного двучлена
Подинтегральное выражение содержит дробные степени линейного двучлена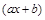 
. В этом случае целесообразно сделать подстановку 
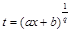, где q – общий знаменатель дробных показателей степеней двучлена.
Пример 2.Найти интеграл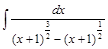 
.
Решение. Пусть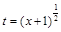 
, 
, 
, 
.
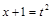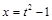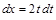Поэтому
.
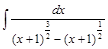
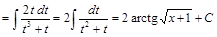