Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений

Правило решения произвольной системы линейных уравнений:

1) Найти ранги основной и расширенной матриц системы, если 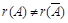, то система несовместна;

2) Если 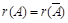, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные 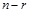неизвестных называют свободными и переносят в правые части уравнений;

3) Найти выражения главных неизвестных через свободные. Получено общее решение системы.

4) Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.

Пример 1. Исследовать на совместность систему

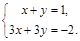
Решение. , .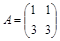

, .

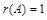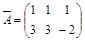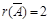
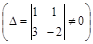Таким образом, 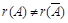, следовательно, система несовместна.

Пример 2. Решить систему

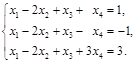
Решение. 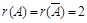. Берем два первых уравнения:

;

; ; .

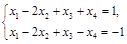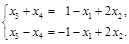
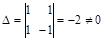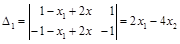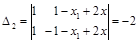Следовательно, 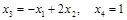– общее решение. Положив, например 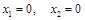, получаем одно из частных решений: .

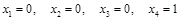Матричный способ решения системы

Рассмотрим решение системы трех линейных уравнений с тремя неизвестными матричным способом.

Используя правила умножения матриц, данную систему уравнений можно записать в виде АХ = В , где

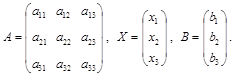
Пусть матрица А невырожденная, т.е. 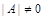. Умножая обе части матричного уравнения слева на матрицу 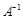, получим обратную матрицы А: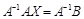

Учитывая, что 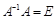, имеем .

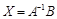Пример 1. Решить систему уравнений матричным способом:

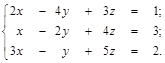
Решение.Обозначим матрицы:

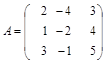– коэффициенты при неизвестных;

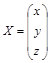– столбец неизвестных; 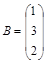– столбец свободных членов.

Тогда систему можно записать матричным способом: АХ = В , где 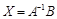. Найдем обратную матрицу .

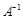а) вычислим определитель матрицы:

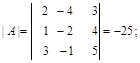
б) найдем алгебраические дополнения элементов матрицы:

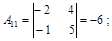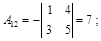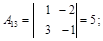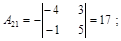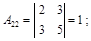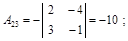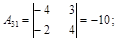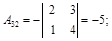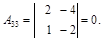Тогда обратная матрица имеет вид

,

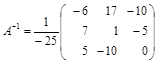итак,

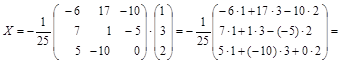
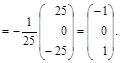
Откуда:

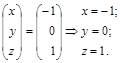
Правило Крамера

Если основной определитель 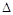матрицы А неоднородной системы п линейных алгебраических уравнений с п неизвестными не равняется нулю, то эта система имеет единственное решение, которое находится по формуле

,

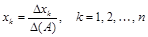где 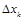— вспомогательный определитель, который получается из основного определителя 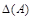путем замены его k-го столбца столбцом свободных членов системы.

Рассмотрим решение системы трех линейных уравнений из тремя неизвестными методом Крамера:

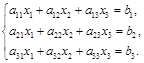
Для нахождения 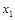, , 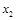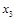применим формулы Крамера:

, , ,

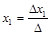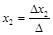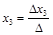где 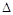– определитель системы, элементы которого есть коэффициенты при неизвестных:

.

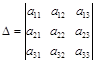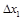получен путем замены первого столбца определителя 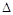столбцом свободных членов:

. ; .

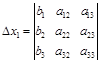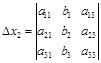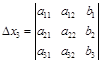Пример 2. Решить систему уравнений по правилу Крамера:

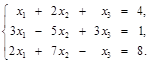
Решение.а) Вычисляем определитель матрицы системы, раскладывая его по первой строке

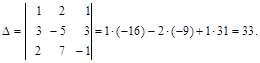
Так как 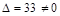не равняется нулю, то система уравнений имеет единственное решение.

б) Вычисляем определители

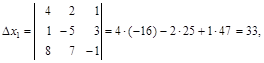
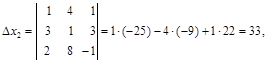
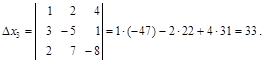
в) По формулам Крамера находим решение системы уравнений

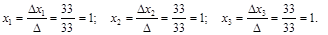
Метод Гаусса

Основная идея метода Гаусса заключается в последовательном исключении неизвестных. Объясним содержание этого метода на системе трех уравнений из тремя неизвестными:

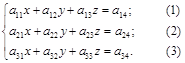
Допустим, что 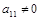(если 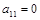, то изменим порядок уравнений, выбрав первым уравнением то, в котором коэффициент при х не равняется нулю).

Первый шаг:

а) делим уравнение (1) на ;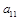

б) множим полученное уравнение на 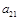и отнимаем с (2);

в) потом множим на 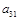и отнимаем с (3).

В результате первого шага будем иметь систему:

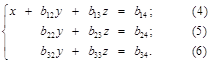
причем ; .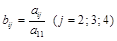

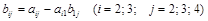Второй шаг: поступаем с уравнениями (5) и (6) точно так же, как с уравнениями (1), (2), (3).

В итоге исходная система приводится к ступенчатому виду:

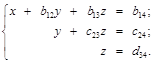
Из преобразованной системы все неизвестные определяются последовательно без проблем.

Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов.

Пример 3. Решить методом Гаусса систему:

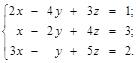
Решение. Переход от одной матрицы к другой будем записывать с помощью знака эквивалентности ~:

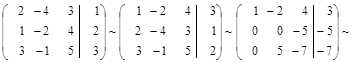
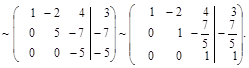
По полученной матрице выписываем преобразованную систему:

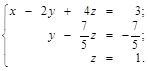
Тогда: ; ; .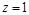

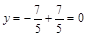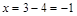Если система имеет единое решение, то ступенчатая система приводится к треугольной, т.е. к такой, в которой последнее уравнение будет содержать одно неизвестное. В случае неопределенной системы, т.е. такой, в которой число неизвестных больше числа линейно независимых уравнений, треугольной системы не будет, так как последнее уравнение будет содержать больше одного неизвестного (система имеет бесчисленное множество решений).

Если система несовместна, то, после приведения ее к ступенчатому виду, она будет содержать хотя бы одно уравнение вида 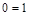, т.е. уравнение, в котором все неизвестные имеют нулевые коэф-фициенты, а правая часть отлична от нуля (система решений не имеет).

Метод Гаусса применим к произвольной системе линейных уравнений (при любых m и n).