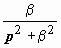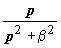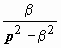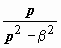Множества на комплексной плоскости
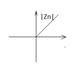
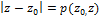
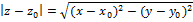
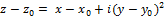
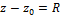 уравнение окружности в т z0 – центр.
уравнение окружности в т z0 – центр.
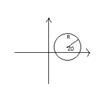
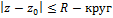
Опр. ε-окрестностью т. Z0 называется множество т. Z, удовлетворяющих неравенству:
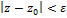
Т.е. это открытый круг с центром в т. Z и радиусом ε.
Пусть определено некоторое множество Е.
Точка Z называется внутренней точкой множества Е, если ∃ ε-окрестности этой точки целиком лежащая в Е.
Множество Е у которого все точки внутренние, называется открытым.
Множество Е называется связным, если 2 любые его точки можно соединить непрерывной кривой лежащей во множестве.
Связное открытое множество называется областью
Пусть дано множество Е.
Множество всех граничных точек множества, называется его границей.
Область вместе с присоединенной границей называется замкнутой областью.
Область называется односвязной если ее граница состоит из 1 непрерывно замкнутой кривой.
Область называется n – связной, если ее граница состоит из n. непрерывных, непересекающихся кривых.
9. Функция комплексного переменного. Предел и непрерывность функции комплексного переменного. Дифференцируемость функции комплексного переменного. Производная. Необходимое и достаточное условия дифференцируемости.
Если каждому комплексному числу z из некот. Области D zэD поставить в соответиствии 1 или неск. Комплексных чисел w по какому то закону z → w(f над стрелкой), то говорят что задана ф-я комплексного переменного. При этом D наз-ся областью определения ф-ии, w- значением ф-ии.
Если каждому числу z w=f(z) поставлено в соотв-ии единств-е число w, то область наз-ся однозначной, в противоположном случае-многозначной. Если однозначная ф-я такова, что 2-ум разл. Значениям z соотв-ют различные значения w, то такая ф-я наз-ся однолистной.
Непрерывность ФКП. Пусть функция w = f(z) определена в окрестности точки z0 = x0 + iy0. Функция называется непрерывной в точке z0, если:
1. существует 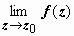 ;
;
2. 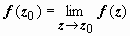
Предел ФКП. Ф-я f(z) имеет предел при z→z0 =x0 + iy0 , если сущ-ют пределы
Lim u(x,y)=u0(при x→x0, y→y0)
Lim v(x,y)=v0(при x→x0, y→y0)
Если ф-я двух перем. u(x,y) имеет предел в т.(x0,y0), то этот предел не зависит от направления.
Дифференцируемость функции комплексной переменной
.Пусть w = f(z) определена, однозначна и принимает собственные значения в окрестности точки z = x + iy ∈ C. Производной функции w = f(z) в точке z называется предел 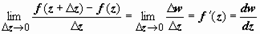 . Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.
. Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.
Однозначная функция называется аналитической в точке z, если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитической в области D,если она аналитична в каждой точке этой области
Необходимость условия дифференцируемости:
Пусть функция f(z) диф. В точке z0 , т.е. существует 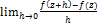 ,
,
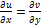
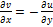
Достаточность условия дифференцируемости:
Условия Коши-Риммана выполнено 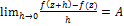
10 . Ряды с комплексными членами. Степенные ряды. Представление основных элементарных функций при помощи рядов. Показательная и логарифмическая функции. Обратные тригонометрические и обратные гиперболические функции.
a1+a2+…+an+.. Числовой ряд может быть составлен из комплексных членов z1+z2+…+zn+...;Sn= 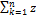 k;
k; 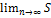 n=S=A+iB. Если каждый член ряда может быть представлен в виде zn=xn+iyn, т. е. x1+iy1=z1..;z1+z2+…+zn+..(1) наш ряд может быть разложен в 2 ряда x1+x2+…+xn+...+i(y1+y2+…+yn+..). Теор. Ряд с комплексными членами (1) сх-ся тогда и только тогда, когда сх-ся ряды, составленные из действительных и мнимых частей членов исходного ряда
n=S=A+iB. Если каждый член ряда может быть представлен в виде zn=xn+iyn, т. е. x1+iy1=z1..;z1+z2+…+zn+..(1) наш ряд может быть разложен в 2 ряда x1+x2+…+xn+...+i(y1+y2+…+yn+..). Теор. Ряд с комплексными членами (1) сх-ся тогда и только тогда, когда сх-ся ряды, составленные из действительных и мнимых частей членов исходного ряда 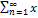 n;
n; 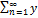 n. Пусть дан ряд z1+z2+…+zn+… (1). Если ряд, составленный из |z1|+|z2|+…+|zn|+...(2) сх-ся, то исходный ряд также сх-ся. При этом ряд (1) называется абсолютно сх-ся. Док-во: |zn|=
n. Пусть дан ряд z1+z2+…+zn+… (1). Если ряд, составленный из |z1|+|z2|+…+|zn|+...(2) сх-ся, то исходный ряд также сх-ся. При этом ряд (1) называется абсолютно сх-ся. Док-во: |zn|= 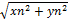 ; |zn|=
; |zn|= 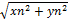 ≥|xn|; |zn|≥|yn| . Ряд из комплексных членов сх-ся, но ряд, составленный из их модулей расх-ся (возможна и такая ситуация), в этом случае исходный ряд –условно сх-ся. Т. к. ряд, составленный из модулей является рядом с действительными членами, то для абсолютной сх-ти ряда (1) применимы известные признаки сх-ти: 1) q=
≥|xn|; |zn|≥|yn| . Ряд из комплексных членов сх-ся, но ряд, составленный из их модулей расх-ся (возможна и такая ситуация), в этом случае исходный ряд –условно сх-ся. Т. к. ряд, составленный из модулей является рядом с действительными членами, то для абсолютной сх-ти ряда (1) применимы известные признаки сх-ти: 1) q= 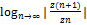 ; q<1сх-ся абсол. q>1расх-ся. 2) q=
; q<1сх-ся абсол. q>1расх-ся. 2) q= 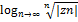 q<1 q>1. C0+C1(z-z0)+…+Cn(z-z0)n+…(3)-степенной ряд. Если (3) сх-ся в т. z1, то он абсолютно сх-ся во всех точках z, которые удовлетворяют неравенству |z-z0|<|z1-z0|. Если (3) расх-ся в т. z2, то он расх-ся во всех точках z, для которых выполняется неравенство |z-z0|>|z2-z0|. z2=z*z; z2*z=z3; ez=ex+iy; eiy=cosy+isiny; ez=ex(cosy+isiny); ez=1+z+
q<1 q>1. C0+C1(z-z0)+…+Cn(z-z0)n+…(3)-степенной ряд. Если (3) сх-ся в т. z1, то он абсолютно сх-ся во всех точках z, которые удовлетворяют неравенству |z-z0|<|z1-z0|. Если (3) расх-ся в т. z2, то он расх-ся во всех точках z, для которых выполняется неравенство |z-z0|>|z2-z0|. z2=z*z; z2*z=z3; ez=ex+iy; eiy=cosy+isiny; ez=ex(cosy+isiny); ez=1+z+ 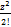 +…=
+…= 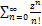 . Используя ряды Маклорена для элементарной ф-ии мы можем определить соответствующую ф-ию для комплексного переменного. ---.Опр. Число w называется логарифмом комплексного числа z если z=ew при этом об-ют w=Lnz. Пусть число z=|z|(cosφ+isinφ)=|z|eiφ ; w=|w|(cosψ+isinψ)=|w|eiψ=u+iv; z=|z|eiφ=eu+iv
. Используя ряды Маклорена для элементарной ф-ии мы можем определить соответствующую ф-ию для комплексного переменного. ---.Опр. Число w называется логарифмом комплексного числа z если z=ew при этом об-ют w=Lnz. Пусть число z=|z|(cosφ+isinφ)=|z|eiφ ; w=|w|(cosψ+isinψ)=|w|eiψ=u+iv; z=|z|eiφ=eu+iv 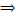 |z|(cosφ+isinφ)=en(cosu+isinv); |z|=eu: v=φ+2πk; u=ln|z|; Lnz=ln|z|+i(argz+2πk). zn=enlnz Для 2-х комплексных чисел z,α общей степенной ф-ей zα=eαlnz.arccosz=iLn(z+
|z|(cosφ+isinφ)=en(cosu+isinv); |z|=eu: v=φ+2πk; u=ln|z|; Lnz=ln|z|+i(argz+2πk). zn=enlnz Для 2-х комплексных чисел z,α общей степенной ф-ей zα=eαlnz.arccosz=iLn(z+ 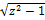 ); arshz=Ln(z+
); arshz=Ln(z+ 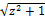 ); arthz=
); arthz=  Ln
Ln 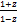 ; arcthz=
; arcthz=  Ln
Ln 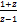 ; ez+2πi=ez. Любой вертикальный отрезок с абц.λ высотой 2π ф-ии ez отображается в окружность с центром в начале координат с радиусом eλ. Полубесконечная горизонтальная полоса (x≥0) шириной 2π ф-ии ez отображается во внешность круга радиусом 1
; ez+2πi=ez. Любой вертикальный отрезок с абц.λ высотой 2π ф-ии ez отображается в окружность с центром в начале координат с радиусом eλ. Полубесконечная горизонтальная полоса (x≥0) шириной 2π ф-ии ez отображается во внешность круга радиусом 1
11 .Интеграл от функции комплексного переменного по дуге. Сведение к определенному интегралу.
(граф.с дугой АВ) Пусть в области G комплексной плоскости лежит дуга 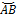 и пусть в этой области определена ф-ия комплексного переменного f(z), разобьем
и пусть в этой области определена ф-ия комплексного переменного f(z), разобьем 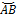 точками z0=A, z1,z2,…,zn=B на n частей. Пусть zk=xk+iyk на каждой из получившихся маленьких дуг произвольным образом выберем произвольную точку Śk. Вычислим значение ф-ии в этой т. f(Śk)=uk+ivk, также Δzk=zk-zk-1=xk+iyk-xk-1-iyk-1=(xk-xk-1)+i(yk-yk-1)=Δxk+iΔyk. Найдем произведение и составим сумму f(Śk)=Δzk;Sn=
точками z0=A, z1,z2,…,zn=B на n частей. Пусть zk=xk+iyk на каждой из получившихся маленьких дуг произвольным образом выберем произвольную точку Śk. Вычислим значение ф-ии в этой т. f(Śk)=uk+ivk, также Δzk=zk-zk-1=xk+iyk-xk-1-iyk-1=(xk-xk-1)+i(yk-yk-1)=Δxk+iΔyk. Найдем произведение и составим сумму f(Śk)=Δzk;Sn= 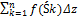 k (1). Сумма (1) – интеграл. сумма для ф-ии f(Śk) по дуге
k (1). Сумма (1) – интеграл. сумма для ф-ии f(Śk) по дуге 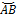 , она очевидно зависит от числа n, способа разбиения дуги на части и способа выбора точек Śk внутри этих частей n
, она очевидно зависит от числа n, способа разбиения дуги на части и способа выбора точек Śk внутри этих частей n 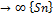 . В том случае, если λ=max|Δzk|
. В том случае, если λ=max|Δzk| 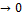 ; k=1,…n.найдем
; k=1,…n.найдем 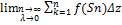 k (2). Если этот предел существует и не зависит от способа разбиения дуги и от способа выбора точек Śk, то он называется интегралом от ф-ии комплексного переменного f(z) вдоль дуги
k (2). Если этот предел существует и не зависит от способа разбиения дуги и от способа выбора точек Śk, то он называется интегралом от ф-ии комплексного переменного f(z) вдоль дуги 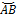 и обозначается
и обозначается 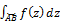 ;
; 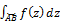 =
= 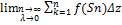 k . Теор. Если кривая l определенная (кусочно-непрерывная, кусочно-гладкая), а f(z) непрерывная, то интеграл (3) существует и равен
k . Теор. Если кривая l определенная (кусочно-непрерывная, кусочно-гладкая), а f(z) непрерывная, то интеграл (3) существует и равен  , где f(z)=u(x,y)+iv(x,y) (4). Замечание: т. к. интеграл от ф-ии комплексного переменного по дуге равен сумме криволинейных интегралов 2го рода, то св-ва этого интеграла должны совпадать со св-ми криволинейного интеграла 2го род:1)
, где f(z)=u(x,y)+iv(x,y) (4). Замечание: т. к. интеграл от ф-ии комплексного переменного по дуге равен сумме криволинейных интегралов 2го рода, то св-ва этого интеграла должны совпадать со св-ми криволинейного интеграла 2го род:1) 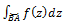 = -
= - 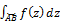 2) если дугу
2) если дугу 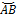 разбить на части точкой С то интеграл по
разбить на части точкой С то интеграл по 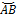 = сумме интегралов:
= сумме интегралов: 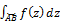 =
= 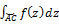 +
+ 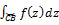 3)Св-во линейности: f(z)=k1f1(z)+k2f2(z)
3)Св-во линейности: f(z)=k1f1(z)+k2f2(z) 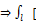 k1f1(z)+k2f2(z)]dz=k1
k1f1(z)+k2f2(z)]dz=k1 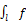 1(z)dz+k2
1(z)dz+k2 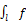 2(z)dz
2(z)dz
12. Теорема Коши для односвязной области. Первообразная. Неопределенный интеграл. Теорема Коши для многосвязной области.
Если D - односвязная ограниченная область, w = f( z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f(z) по L равен нулю: 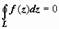 .
.
Доказательство:эта теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 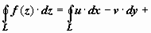
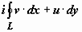 , то, применяя к действительным криволинейным интегралам формулу Грина, получим
, то, применяя к действительным криволинейным интегралам формулу Грина, получим 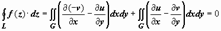 вследствие условий Коши-Римана
вследствие условий Коши-Римана 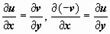 . Символом G в доказательстве обозначена область, заключённая внутри контура L
. Символом G в доказательстве обозначена область, заключённая внутри контура L
Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f(z), и имеющих общие начальную и конечную точки, интеграл 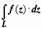 имеет одинаковое значение.
имеет одинаковое значение.
Первообразная:
Если функция f(z) аналитична в некоторой области D
И если аналитическая функция F(z) в этой области удовлетворяет рав-ву 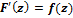 то F(z) называется первообразной для функции f(z) ,
то F(z) называется первообразной для функции f(z) ,
Очевидно для любого C , F(z)+Cтак же будет первообразной . если F1(z) и F2(z) – первообразные для функции f(z), то F1(z)-F2(z)=C=const
Неопр. интеграл :
Пусть на комплексной плоскости С задана ориентированная кусочно-гладкая кривая 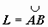 , на которой определена функция w = f(z). Разобьём кривую точками z0 = A, z1, z2, …, zn = B на n частей, на каждой из дуг
, на которой определена функция w = f(z). Разобьём кривую точками z0 = A, z1, z2, …, zn = B на n частей, на каждой из дуг 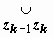 выберем произвольную точку tk, найдём f(tk) и составим интегральную сумму
выберем произвольную точку tk, найдём f(tk) и составим интегральную сумму 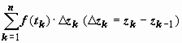 . Предел последовательности этих сумм при n → ∞, max|Δ z k| → 0 (k = 1, 2, ..., n), если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек tk, называется интегралом от функции w = f(z) по кривой L и обозначается
. Предел последовательности этих сумм при n → ∞, max|Δ z k| → 0 (k = 1, 2, ..., n), если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек tk, называется интегралом от функции w = f(z) по кривой L и обозначается 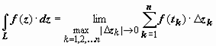 .
.
Теорема. Если функция w = f(z) непрерывна на кривой L, то она интегрируема по этой кривой.
Док-во. Распишем действительные и мнимые части всех величин, входящих в интеграл: z k = x k + iy k, f( z) = u(x, y) + iv(x, y), t k = ξ k + iζ k, Δzk = zk − zk -1 = (xk + iyk) − (xk -1 + iyk -1) = (xk − xk -1) + i(yk − yk -1) = Δx k + iΔy k, тогда f(t k)·Δz k = (u(ξk, ζk) + iv(ξk, ζk))(Δxk + i Δyk) = (u(ξk, ζ kk)·Δx k − v(ξk, ζk)·Δy k) + i (u(ξk, ζk)·Δy k + v(ξk, ζk)·Δx k), и сумма 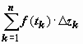 разобьётся на две
разобьётся на две 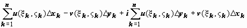 . Каждая из этих сумм - интегральная сумма для действительных криволинейных интегралов второго рода, соответственно,
. Каждая из этих сумм - интегральная сумма для действительных криволинейных интегралов второго рода, соответственно, 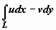 и
и 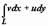 . Если L - кусочно-гладкая кривая, w = f(z) - непрерывна (тогда непрерывны её координатные функции u(x, y) и v(x, y)), то существуют пределы этих сумм при max|Δzk| → 0 (k = 1, 2, 3, ..., n) - соответствующие криволинейные интегралы, следовательно, существует
. Если L - кусочно-гладкая кривая, w = f(z) - непрерывна (тогда непрерывны её координатные функции u(x, y) и v(x, y)), то существуют пределы этих сумм при max|Δzk| → 0 (k = 1, 2, 3, ..., n) - соответствующие криволинейные интегралы, следовательно, существует 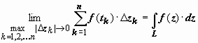 , и
, и 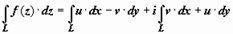 .
.
Теорема Коши для многосвязной области:
Если функция w = f(z) аналитична в замкнутой многосвязной ограниченной области 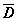 , ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области
, ограниченной контурами L0 (внешняя граница), L1, L2, …, Lk, то интеграл от f(z), взятый по полной границе области 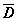 , проходимой так,что область остаётся с одной стороны, равен нулю.Доказательство и здесь воспроизводит доказательство формулы Грина для многосвязной области. Рассмотрим случай, когда граница области
, проходимой так,что область остаётся с одной стороны, равен нулю.Доказательство и здесь воспроизводит доказательство формулы Грина для многосвязной области. Рассмотрим случай, когда граница области 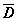 (на рисунке область заштрихована) состоит из внешнего контура L0 и внутренних контуров L1 и L2. Соединим контур L0разрезом FM с контуром L1, разрезом BG - с контуром L2. Область
(на рисунке область заштрихована) состоит из внешнего контура L0 и внутренних контуров L1 и L2. Соединим контур L0разрезом FM с контуром L1, разрезом BG - с контуром L2. Область 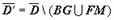 с границей
с границей 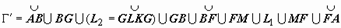 односвязна, поэтому для неё справедлива интегральная теорема Коши:
односвязна, поэтому для неё справедлива интегральная теорема Коши: 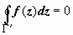 . Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.
. Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.
В дальнейшем нам понадобится другая формулировка этой теоремы. Буквами без верхнего индекса будем обозначать контуры, проходимые против часовой стрелки, с верхним минусом - по часовой. Мы доказали, что 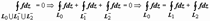 . Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.
. Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.
13. Интегральная формула Коши. Формула Коши для старших производных. Теорема Морера. Ряд Тейлора.
Пусть функция f(z) аналитична в многосвязной области D. Тогда интеграл по любому составному контуру Г лежащему в области D равной 0
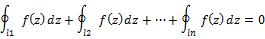
Следствие 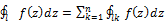
Теорема Морера
Если ф-ия f(z) непрерывна в односвязной области D и интеграл от этой ф-ии по любому замкнутому контуру, целиком лежащему в этой области равной 0, то ф-ия f(z) аналитична в этой области D
Ряд Тейлора
Пусть ф-ия f(z) аналитична в некоторой области D и пусть в этой области задана l ограничивающая некоторую область w.
Тогда ряд 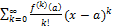 Называется рядом Тейлора ф-ии f в точке а.
Называется рядом Тейлора ф-ии f в точке а.
14. Ряд Лорана. Свойства ряда Лорана. Кольцо сходимости.
Теор. Пусть ф-ия f(z) аналитическая в кольце 0≤r<|z-z0|<R< 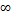 , тогда всюду в этом кольце она раскладывается в ряд f(z)=
, тогда всюду в этом кольце она раскладывается в ряд f(z)=  (3) при этом Ck=
(3) при этом Ck= 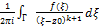 (4), здесь Г – простой замкнутый контур, лежащий внутри кольца. Опр. Ряд (3) называется рядом Лорана для ф-ии f(z). Св-ва: 1.
(4), здесь Г – простой замкнутый контур, лежащий внутри кольца. Опр. Ряд (3) называется рядом Лорана для ф-ии f(z). Св-ва: 1. 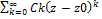 -называется рядом, входящим в правую часть ф-лы (3) – правильная часть ряда Лорана. Он сх-ся всюду внутри внешней окружности кольца аналитичности. 2.
-называется рядом, входящим в правую часть ф-лы (3) – правильная часть ряда Лорана. Он сх-ся всюду внутри внешней окружности кольца аналитичности. 2. 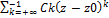 - входящий в правую часть формулы (3) – главная часть ряда Лорана. Он сх-ся всюду, вне внутренней окружности кольца аналитичности. 3. Ряд Лорана сх-ся во всех точках кольца аналитичности, которое называется при этом кольцом сх-ти. 4. Всюду в кольце сх-ти ряд Лорана можно почленно интегрировать, а также дифференцировать сколько угодно раз. 5. Разложение ф-ии в ряд Лорана в каждом кольце единственно, т. е. если существует ряд f(z)=
- входящий в правую часть формулы (3) – главная часть ряда Лорана. Он сх-ся всюду, вне внутренней окружности кольца аналитичности. 3. Ряд Лорана сх-ся во всех точках кольца аналитичности, которое называется при этом кольцом сх-ти. 4. Всюду в кольце сх-ти ряд Лорана можно почленно интегрировать, а также дифференцировать сколько угодно раз. 5. Разложение ф-ии в ряд Лорана в каждом кольце единственно, т. е. если существует ряд f(z)= 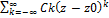 , то контуры Ck опред-ся формулой (4)
, то контуры Ck опред-ся формулой (4)
.
15. Изолированные особые точки. Разложение функции в ряд Лорана в окрестности изолированной особой точки.
Опр. т. z0 называется особой точкой т. функции f(z), если в этой точке аналитическая функция
теряет свою аналитичность.
Особая точка z0 называется изолированной особой точкой , если функция f(z) аналитична всюду в кольце 0 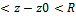 , а в т. z0 теряет свою аналитичность .
, а в т. z0 теряет свою аналитичность .
Z0=0 0 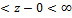
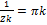
Zk= 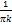
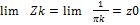
Опр. Изолированая особая точка z0 называется устранимой особой точкой функции f(z) аналитической в кольце 0 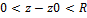 , если
, если 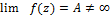
Опр. Изолированая особая точка называется полюсом функции f(z), аналитической в кольце 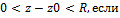
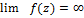
Опр. Изолированая особая точка z0 называется сущетсвенной особой точкой функции f(z),аналитической в кольце 0  .
.
Устранимая особая точка и точка и разложения функции в ряд Лорана в окрестностях устранимой особой точки.
Теорема. Изолированая особая точка z0 является устранимой особой точки функции f(z) тогда и только тогда , когда разложения функции f(z) в окрестности этой точки не содержит главной части т.е.,ряд Лорана состоит из правильной части.
Дост-сть
Пусть так и есть

Тогда 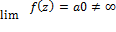
Необх-сть
Пусть т.z0 является устранимой особой точкой.
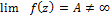
f(z) 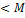 , в некотрой окрестности z0
, в некотрой окрестности z0 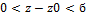
16. Вычет функции. Теорема о вычетах. Вычисление вычетов. Вычет функции в бесконечно удаленной точке.
Теорема: если т. Z0 – полюс 1-ого порядка ф-ии f(z), т.е. фун-я представится в виде
F(z) = 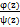 при этом
при этом 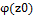
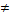 0 ,
0 , 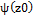 =0 ,
=0 , 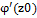
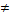 0 , тогда вычет функции res Z0 f(z)=
0 , тогда вычет функции res Z0 f(z)= 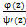
res Z0 f(z)= 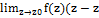 0)=
0)= 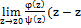 0) =
0) = 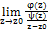 =
= 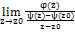 =
=
= 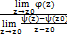 =
= 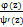
Вычет в бесконечно удаленной особой точке.
Z= 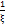 f (
f ( 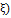 =f
=f 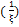
f(z) =a0 + a1z + a2z + …
f ( 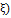 =a0 + a1
=a0 + a1 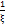 +a2
+a2 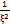 + …
+ …
res Z0 f(z) = 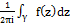
f(z) = 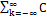 k Zk
k Zk
res Z0 f(z)= 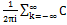 k
k 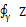 k dz =
k dz = 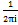 ( -2
( -2 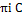 -1) = - C–1
-1) = - C–1
Вычет функции в бесконечно удаленной точке равен коэффициенту С-1 со знаком – разложения функции в ряд Лорана по степеням z
17. Применение вычетов к вычислению определенных и неопределенных интегралов.
Вычисление несобственных интегралов при помощи вычетов.
Пусть требуется найти 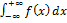
Теорема. Пусть функция f(z) аналитична в верхней полуплоскости, включая действительную ось, за исключением конечного числа особых точек z1, z2, … zn лежащих в верхней полуплоскости.
|z|≥R
|f(z)|= 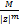 , где m≥z
, где m≥z
R – такое, что все особые m попадают внутрь окружности радиуса R.
Тогда 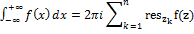
18. Логарифмический вычет. Принцип аргумента. Теорема Руше. Основная теорема алгебры.
Лог. Выч.Опр. Лог-ой производной ф-ии называется производная логарифма от этой ф-ии. Опр. Лог-им вычетом ф-ии f(z)называется вычет от лог-ой производной этой ф-ии: 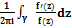 . Из опр. следует, что лог-ий вычет имеет место не только в особых точках ф-ии, но и в нулях. Теор. В полюсах и нулях ф-ии f(z) лог-ая производная имеет простые полюсы. Лог-ий вычет в нуле ф-ии равен порядку этого нуля. Лог-ий вычет в полюсе ф-ии равен порядку полюса, взятому со знаком «-». Док-во: f(z) имеет в т. z0 нулю порядка n. f(z)=an(z-z0)n+an+1(z-z0)n+1+…; f’(z)= ann(z-z0)n-1+an+1(n+1)(z-z0)n+…; f’(z)/f(z)=…=χ(z)/(z-z0); χ(z)=φ(z)/ψ(z); φ(z)=ann+an+1(n+1)(z-z0)+…; ψ(z)=an+an+1(z-z0)+…; φ(z0)=ann; ψ(z0)=an; χ(z)-также будет аналитической, причем χ(z0)≠0; χ(z)=n+b1(z-z0)+…;
. Из опр. следует, что лог-ий вычет имеет место не только в особых точках ф-ии, но и в нулях. Теор. В полюсах и нулях ф-ии f(z) лог-ая производная имеет простые полюсы. Лог-ий вычет в нуле ф-ии равен порядку этого нуля. Лог-ий вычет в полюсе ф-ии равен порядку полюса, взятому со знаком «-». Док-во: f(z) имеет в т. z0 нулю порядка n. f(z)=an(z-z0)n+an+1(z-z0)n+1+…; f’(z)= ann(z-z0)n-1+an+1(n+1)(z-z0)n+…; f’(z)/f(z)=…=χ(z)/(z-z0); χ(z)=φ(z)/ψ(z); φ(z)=ann+an+1(n+1)(z-z0)+…; ψ(z)=an+an+1(z-z0)+…; φ(z0)=ann; ψ(z0)=an; χ(z)-также будет аналитической, причем χ(z0)≠0; χ(z)=n+b1(z-z0)+…; 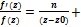 b1+…;Пустьz0 – полюс ф-ии f(z)порядка Р. f(z)=1/g(z), где g(z) имеет в т. z0 нуль порядка Р. Тогда (lnf(z))’=-(lng(z))’ .
b1+…;Пустьz0 – полюс ф-ии f(z)порядка Р. f(z)=1/g(z), где g(z) имеет в т. z0 нуль порядка Р. Тогда (lnf(z))’=-(lng(z))’ .
Прин. арг.Теор. Пусть ф-ия f(z) аналитическая в области D всюду за исключением конечного числа полюсов z1,z2,…,zk и p1,p2,…,pkи пусть ф-ия f(z) непрерывна на границе области Г, нигде на этой границе не обращается в нулю, а внутри обл. Dимеет лишь конечное число нулей a1,a2,…,am порядков n1,n2,…,nm. Тогда справедливо следующее выражение: 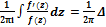 Гargf(z)=N-P (2). Здесь N= n1+n2+…+nm - общее число нулей с учетом их кратности; P= p1+p2+…+pk - общее число полюсов с учетом их порядка, ΔГargf(z) - приращение аргумента ф-ии при обходе вдоль контура Г.
Гargf(z)=N-P (2). Здесь N= n1+n2+…+nm - общее число нулей с учетом их кратности; P= p1+p2+…+pk - общее число полюсов с учетом их порядка, ΔГargf(z) - приращение аргумента ф-ии при обходе вдоль контура Г.  ΔГargf(z)=
ΔГargf(z)= 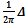 Гargf(z);
Гargf(z); 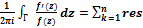 Zk
Zk 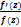 =n1+n2+…+nm-p1-p2-…-pk=N-P.Следствие1: если ф-ия аналитическая внутри контура γ, то
=n1+n2+…+nm-p1-p2-…-pk=N-P.Следствие1: если ф-ия аналитическая внутри контура γ, то 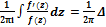 Гargf(z)=N. Следствие2: число оборотов ф-ии при
Гargf(z)=N. Следствие2: число оборотов ф-ии при
обходе контура является целым число. Руше. Теор. Пусть ф-ии f(z)иg(z) аналитические внутри контура γ, а на самом контуре удовлет. неравенству|f(z)|>|g(z)|, тогда ф-ии f(z)и f(z)+g(z) имеет внутри контура одинаковое число нулей. |f(z)|>|g(z)|≥0; |f(z)|>0; |f(z)+g(z)|≥|f(z)-g(z)|>0; f(z)и f(z)+g(z)не обращается вна контуре в нуль. ΔГarg(f(z)+g(z))=ΔГargf(z)(1+ 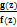 )= ΔГ(argf(z)+arg(1+
)= ΔГ(argf(z)+arg(1+ 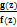 ))= ΔГargf(z)+ ΔГarg(1+
))= ΔГargf(z)+ ΔГarg(1+ 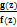 )= ΔГargf(z)=2πiN. Осн. Теор. Алг. Ур-е a0xn+a1xn-1+…+an-1x+an=0 (3) имеет в комплексной плоскости ровно n корней. Док-во: Рассмотрим f(z)=a0zn; g(z)=a1zn-1+…+an. Возьмем окружность радиусаR достаточно большого, такого чтобы многочлен g(z) не имел вне этой окружности корней и чтобы выполнялось неравенство |f(z)|>|g(z)|. Очевидно это можно сделать, т. к. степенная ф-ия zn растет быстрее, чем любой многочлен меньшей степени. Тогда по Теор. Руше ф-ия f(z)и f(z)+g(z) имеют одинаковое число нулей внутри этой окружности.
)= ΔГargf(z)=2πiN. Осн. Теор. Алг. Ур-е a0xn+a1xn-1+…+an-1x+an=0 (3) имеет в комплексной плоскости ровно n корней. Док-во: Рассмотрим f(z)=a0zn; g(z)=a1zn-1+…+an. Возьмем окружность радиусаR достаточно большого, такого чтобы многочлен g(z) не имел вне этой окружности корней и чтобы выполнялось неравенство |f(z)|>|g(z)|. Очевидно это можно сделать, т. к. степенная ф-ия zn растет быстрее, чем любой многочлен меньшей степени. Тогда по Теор. Руше ф-ия f(z)и f(z)+g(z) имеют одинаковое число нулей внутри этой окружности.
19. Преобразование Лапласа и его свойства. Оригинал и изображение. Дифференцирование и интегрирование оригинала и изображения.
Для произвольного комплексного числа S и произвольного оригинала f(t) преобразование 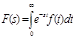 называется интегральным преобразованием Лапласа.
называется интегральным преобразованием Лапласа.
f1(t) .=. F1(s) ; f2(t) .=. F2(s)
Cв-ва: 1) c*f1(t) .=. c*F1(s)
2) f1(t) + f2(t) .=. F1(s) + F2(s)
Будем действительную функцию действительного аргумента f(t) называть оригиналом, если она удовлетворяет трем требованиям:
1. 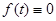 при t < 0
при t < 0
2. 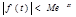 при t > 0, M > 0,
при t > 0, M > 0, 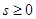
3. На любом конечном отрезке [ab ] , положительный полуоси Ot функция f(t) удовлетворяет условиям Дирихле, т.е.
a) ограничена,
b) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода,
c) имеет конечное число экстремумов.
Функции, удовлетворяющие этим трем требованиям, называются в операционном исчислении изображаемыми по Лапласу или оригиналами.
Дифференцирование оригинала:
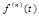
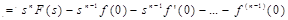
Дифференцирование изображения:
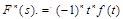
Интегрирование оригинала:
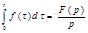
Интегрирование изображения
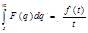
20. Функция Хевисайда. Теорема смещения. Теорема запаздывания. Теорема подобия. Свертка функций. Изображение основных элементарных функций.
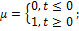 называется функцией Хевисайда или единичной функцией Хевисайда.
называется функцией Хевисайда или единичной функцией Хевисайда.
Теорема смещения:
Если f (t) 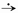 F(p), то e α t f (t)
F(p), то e α t f (t) 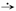 F(p − α),. Здесь α - произвольное комплексное число.
F(p − α),. Здесь α - произвольное комплексное число.
Док-во. 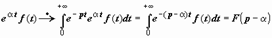
Теорема запаздывания :
Если f (t) 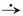 F( p) (т.е. f (t) · η(t)
F( p) (т.е. f (t) · η(t) 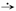 F( p)), то f (t − t0) · η(t − t0)
F( p)), то f (t − t0) · η(t − t0) 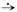 e −t0 · p · F( p) для любого числа t0 ≥ 0.
e −t0 · p · F( p) для любого числа t0 ≥ 0.
Док-во. 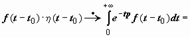
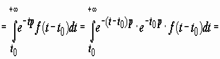
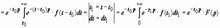
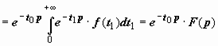
Теорема подобия: Если f (t) - функция-оригинал и f (t) 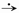 F(p), то для любого λ > 0
F(p), то для любого λ > 0 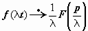 .
.
Док-во. 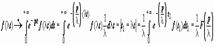 .
.
Иллюстрации применения этого свойства: если 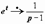 , то
, то 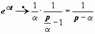 ; если
; если 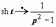 , то
, то 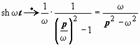 и т.д
и т.д
Свертка функции: Сверткой функций f1(t) и f2(t) называется функция 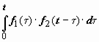 .
.
Свёртка обозначается символом f1 * f2: 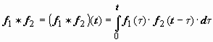 . Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригиналСвёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле
. Если f1(t) и f2(t) - функции-оригиналы, то их свёртка - тоже функция-оригиналСвёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле 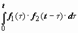 переменную τ на τ1 = t −τ.
переменную τ на τ1 = t −τ.
Можно показать, что свёртка обладает свойством ассоциативности, т.е. что ( f1 * f2 ) * f3 = f1 * ( f2 * f3 )
Изображение основных элементарных функций:
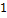
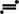 1/S
1/S
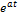
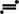
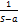
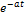
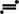
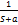
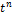
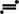
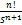
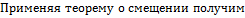
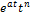
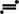
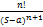
Применяя теорему о подобии получим
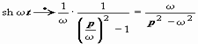
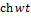
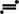
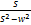
|
21. Восстановление оригинала по рациональному изображению. Решение дифференциальных уравнений и систем операционным методом.
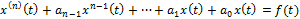
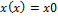 x’(0)=x0,…,
x’(0)=x0,…, 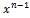 (0)=
(0)= 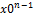
Пусть f(t) 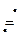 F(s) ; x(t)
F(s) ; x(t) 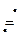
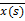 – решение этого у-я
– решение этого у-я