Охарактеризуйте способы определения собственных и взаимных проводимостей
Собственные и взаимные проводимости можно найти различными способами:
1) способом наложения;
2) способом преобразований;
3) способом единичных токов;
4) с помощью матричных методов.
Способ наложения - синхронные машины представляются некоторыми постоянными сопротивлениями с приложенными за ними ЭДС, а асинхронные двигатели – только сопротивлениями. Любая система может быть в этом случае представлена схемой, аналогичной схеме, показанной на рис.
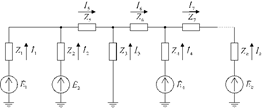
Используя метод наложения, заменим рассмотрение данной схемы рассмотрением ряда подсхем, каждая из которых содержит только один источник ЭДС (например, в первой ветви – рис)
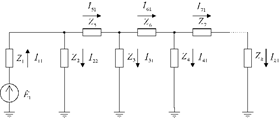
В этом случае ток в первой ветви может быть найден как
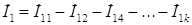 , | (2.5) |
где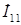 
- собственный ток первой ветви;
, 
,…, 
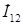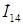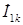- взаимные токи первой ветви и остальных ветвей, содержащих источники ЭДС.
Собственный ток ветви – это составляющая тока в любой ветви, вызванная действием ЭДС, приложенной в данной ветви, при отсутствии ЭДС в других ветвях.
Собственный ток ветви с номером n равен
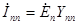 , | (2.6) |
где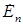 
- ЭДС n-ой ветви;
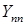- собственная проводимость n-ой ветви, представляющая собой коэффициент пропорциональности между током n-ой ветви и ЭДС этой же ветви при равенстве нулю ЭДС во всех остальных ветвях.
Взаимный ток двух ветвей – это составляющая тока в одной из ветвей, вызванная действием ЭДС в другой ветви при равенстве нулю ЭДС во всех остальных ветвях.
Взаимный ток ветвей n и m равен
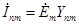 , | (2.7) |
где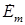 
- ЭДС ветви с номером m;
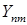- взаимная проводимость ветвей n и m, представляющая собой коэффициент пропорциональности между током ветви n и ЭДС, приложенной в ветви m, при равенстве нулю ЭДС во всех остальных ветвях.
Величины, обратные собственным проводимостям ветвей, называются собственными сопротивлениями ветвей, а величины, обратные взаимным проводимостям ветвей, - взаимными сопротивлениями ветвей.
Способ преобразования - заключается в том, что исходная схема преобразуется к виду схемы, изображенной на рис. 2.10.
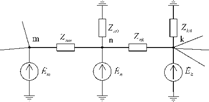
Собственные и взаимные проводимости находятся в этом случае следующим образом:
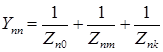 , | (2.9) |
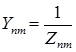 , | (2.10) |
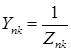 и т.д. | (2.11) |
Способ единичных токов - делается предположение о том, что все ЭДС кроме одной равны нулю. Ток в одной из ветвей принимают равным единице и последовательно находят токи в ветвях и напряжения в узлах схемы при принятых допущениях, а затем определяют величину ЭДС, которая необходима для протекания единичного тока. В качестве примера рассмотрим схему, изображенную на рис. 2.11.
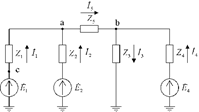
Рис. 2.11. Исходная схема
Будем считать, что все ЭДС, кроме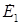 
равны 0, а в ветви 4 протекает ток 
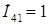(рис. 2.12).
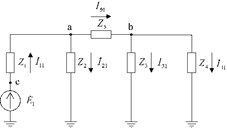
Рис. 2.12. Схема с источником ЭДС в первой ветви
В этом случае напряжение в узле b равно
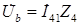 . | (2.12) |
Ток в ветви 3
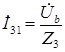 . | (2.13) |
Ток в ветви 5
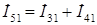 . | (2.14) |
Падение напряжения на сопротивлении ветви 5
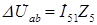 . | (2.15) |
Напряжение в узле a
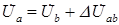 . | (2.16) |
Ток в ветви 2
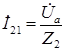 . | (2.17) |
Ток в ветви 1
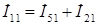 . | (2.18) |
Падение напряжения на сопротивлении ветви 1
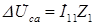 . | (2.19) |
ЭДС ветви 1
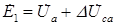 . | (2.20) |
После этого можно определить собственную проводимость первой ветви, а также взаимные проводимости первой и остальных ветвей
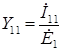 , | (2.21) |
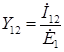 и т.д. | (2.22) |
Для определения остальных собственных и взаимных проводимостей эту процедуру повторяют, последовательно вводя ЭДС во все генераторные ветви.
Матричный метод на основании графа схемы замещения. Например, можно использовать выражение
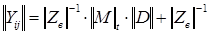 , | (2.23) |
где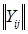 
- матрица собственных и взаимных проводимостей ветвей;
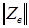- квадратная матрица сопротивлений ветвей, являющаяся при отсутствии взаимной индукции между ветвями диагональной матрицей;
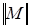- матрица соединений в узлах (первая матрица инциденций);
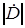- матрица комплексных коэффициентов распределения напряжения, определяемая как
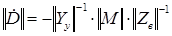 , | (2.24) |
где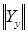 
- матрица узловых проводимостей.
Элементы главной диагонали матрицы 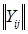являются собственными проводимостями ветвей, а остальные элементы – взаимными проводимостями.