Краткие теоретические сведения. Рассмотрим систему s линейных уравнений с n неизвестными
Рассмотрим систему s линейных уравнений с n неизвестными
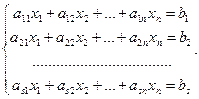 (6.1)
(6.1)
1. Если среди уравнений системы есть уравнения вида 0x1+0x2+...+0xn=bk, где bk¹0, то система уравнений (6.1) несовместна.
2. Пусть в каждом уравнении системы есть хотя бы по одному отличному от 0 коэффициенту. Если a11 =0, то перенумерацией неизвестных добьемся, чтобы первый коэффициент был отличен от нуля. Таким образом, можем считать , что a11¹0.
Исключим теперь слагаемые, содержащие х1, из всех остальных уравнений. Для этого к каждому i-ому (i=2,...,n) уравнению прибавим первое, умноженное на 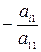 (i=2,...,n).
(i=2,...,n).
продолжим аналогичные рассуждения для переменной х2 (начиная со второго уравнения).
Если в системе уравнений в результате преобразований появились уравнения вида 0x1+0x2+...+0xn=0, то их отбрасываем, а если появилось уравнение вида 0x1+0x2+...+0xn=bk, где bk¹0, то полученная система уравнений , а следовательно и равносильная ей система уравнений (6.1), несовместна.
Если система не содержит уравнений вида 0x1+0x2+...+0xn=bk, где bk¹0, то будем считать, что a22¹0, и исключим х2 из всех оставшихся уравнений, прибавляя к каждому i-ому (i=3,...,n) уравнению второе, умноженное на 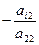 (i=3,...,n). Так как система содержит конечное число уравнений, то процесс исключения неизвестных конечен. То есть через некоторое число шагов мы получим систему уравнений
(i=3,...,n). Так как система содержит конечное число уравнений, то процесс исключения неизвестных конечен. То есть через некоторое число шагов мы получим систему уравнений
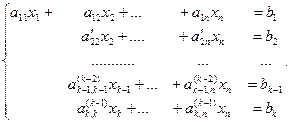 (6.2)
(6.2)
Здесь 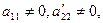 ...,
..., 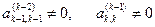 , k£s, и, очевидно, k£n.
, k£s, и, очевидно, k£n.
В этом случае система уравнений (6.2) и, следовательно, система уравнений (6.1) совместны, причем, если k=n, то система имеет единственное решение, а если k<n ,то система уравнений имеет бесконечное множество решений.
Действительно, если k=n, то система имеет вид
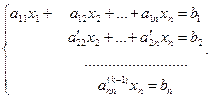 (6.3)
(6.3)
Так как 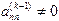 , то из последнего уравнения системы (6.3) найдем xn, подставим найденное значение во все остальные уравнения системы и из предпоследнего уравнения найдем xn-1 и так далее. Все переменные определяются однозначно и система (6.3) и, следовательно, система уравнений (6.1) имеют единственное решение.
, то из последнего уравнения системы (6.3) найдем xn, подставим найденное значение во все остальные уравнения системы и из предпоследнего уравнения найдем xn-1 и так далее. Все переменные определяются однозначно и система (6.3) и, следовательно, система уравнений (6.1) имеют единственное решение.
Если k<n, то система уравнений имеет вид (6.3). Неизвестные хk+1, xk+2, ..., xn объявляем свободными. Этим переменным можно присвоить любые значения и поднимаясь по системе (6.3) снизу вверх, найти значения остальных переменных, которые для данного набора свободных переменных определяются однозначно. Таким образом, давая различные значения свободным переменным хk+1, xk+2,...,xn,получим все решения системы.
Вывод. Метод Гаусса применим к решению любой системы линейных уравнений. При этом система (6.1) будет несовместной, если в процессе преобразований получится уравнение вида 0x1+0x2+...+0xn=bk, где bk¹0,или система будет совместной. Совместная система имеет единственное решение, если k=n, и будет иметь множество решений, если k<n.
Замечание 1. Однородная система уравнений всегда совместна, так как в ней не может быть уравнений вида 0x1+0x2+...+0xn=bk, где bk¹0. Она всегда имеет нулевое решение, а если k<n,то система имеет и ненулевые решения.
Замечание 2. На практике все преобразования производят не над уравнениями системы, а над строками расширенной матрицы системы.
Если b1=b2=…=bs=0, тогда система линейных уравнений имеет вид
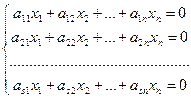 (6.4)
(6.4)
и называется однородной. Очевидно, что однородная система всегда совместна, то есть множество ее решений не пусто. В частности, решением любой однородной системы линейных уравнений будет решение: x1=…=xn=0. Это решение называется нулевым, или тривиальным.
Будем обозначать решение системы (6.4) вектором
xa=(a1, a2, …, an),
то есть xa будет решением системы (6.6), если
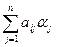 =0, i=1, 2, …, s.
=0, i=1, 2, …, s.
Рассмотрим множество всех решений системы (6.4)
M={xa½xa=(a1, a2, …, an) Ù 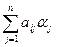 =0, i=1, 2, …, s}.
=0, i=1, 2, …, s}.
Теорема. М - линейное подпространство линейного пространства R(n).
Определение. Базис линейного пространства решений системы линейных однородных уравнений называется фундаментальной системой решений.
