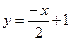Обзор основных элементарных функций
Линейная функция.
Задается формулой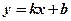 
, где 
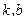– константы, 
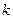– угловой коэффициент наклона прямой, 
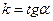, где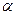 
– угол между прямой и положительным направлением оси абсцисс (см. рис.1). График – прямая линия.
|
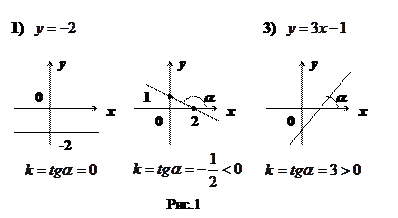
Квадратичная функция.
Задается формулой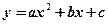 
,где 
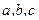– константы. График - парабола. Если 
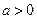, то ветви параболы направлены вверх, если 
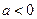– то вниз. Нули х1, х2 функции:
.
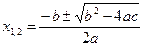Координаты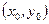 
вершины параболы:
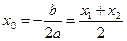; y0=f(x0).
Заметим, что если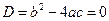 
, то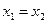 
(два совпадающих корня!).
Пример.
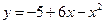. Находим нули функции из уравнения 
: 
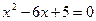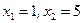. Координаты вершины этой параболы:
; 
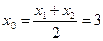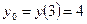. (см. рис.2).
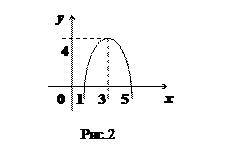
Дробно-линейная функция.
Задается формулой
.
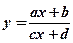
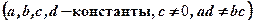График – гипербола. Частный случай: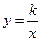 
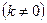– "обратная пропорциональность" (см. рис. 3).
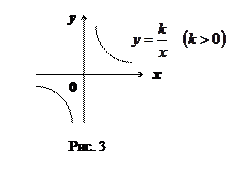
Показательная функция.
Задается формулой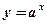 
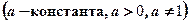(см. рис.4).
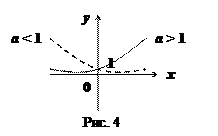
Логарифмическая функция.
Задается формулой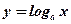
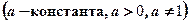(см. рис.5).
Степенная функция.
Задается формулой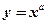
( 
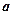– любое действительное число).
1) 
( 
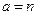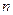– натуральное число) (см. рис.6):
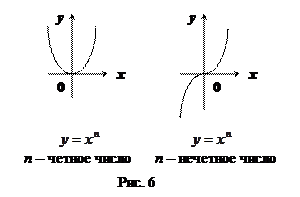
2) 
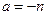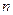( – натуральное число) (см. рис.7):
3) 
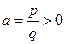– несократимая дробь (см. рис.8):
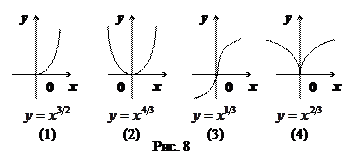
При построении таких графиков надо учитывать четность чисел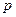 
и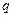 
, а также соотношение между ними ( 
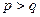или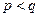 
). Например, если 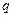чётно, то 
(см. рис.8 (1)), если нечётно, то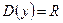 
(см. рис. 8(2)–8(4)). Если 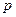чётно, то 
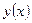– чётная функция; если 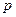нечётно, то 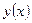– нечётная функция. Если 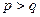, то при 
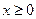график функции ведет себя, как график функции 
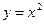, а если 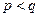- как график функции 
.
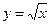7. Функция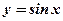 
(см. рис.9).
Нечетная периодическая функция с периодом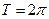 
. Полезно помнить, что:
; 
; 
; 
;
; 
.
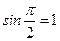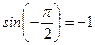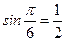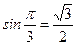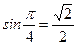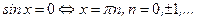8. Функция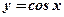 
(см. рис.10).
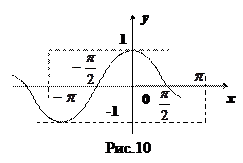
Четная периодическая функция с периодом 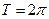. Полезно помнить, что:
; 
; 
; 
;
; 
.
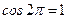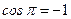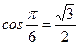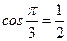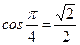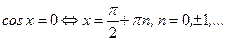9. Функция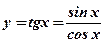 
(см. рис.11).
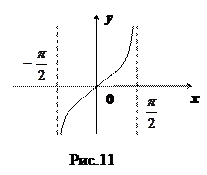
Нечетная периодическая функция с периодом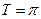 
. Значения функции 
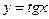в точках 
; 
; 
; 
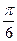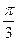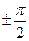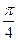и т.д. вычисляются по значениям функци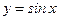й 
и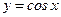 
.
10. Функция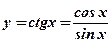 
(см. рис.12).
 |
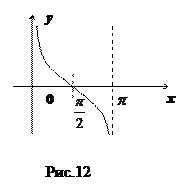Нечетная периодическая функция с периодом 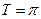. Значения функции 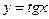в точках 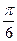; ; 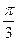; 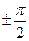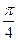и т.д. вычисляются по значениям функци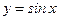й и .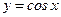
11. Функция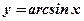 
(арксинус числа 
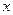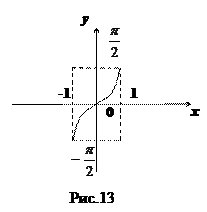
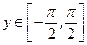– это такое число 
, что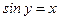 
) (см. рис.13).
12. Функция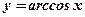 
(арккосинус числа 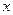– это такое число 
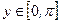, что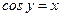 
) (см. рис.14).
 |
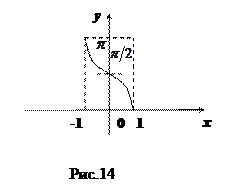13. Функция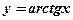 
(арктангенс числа 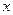– это такое числ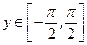о , что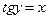 
) (см. рис.15).
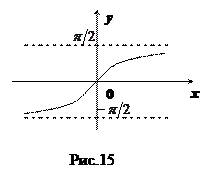
14. Функция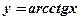 
(арккотангенс числа 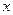– это такое числ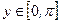о , что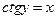 
) (см. рис.16).
 |
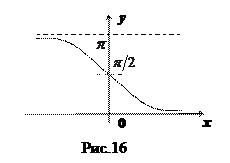Примеры.
1)Найти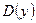 
для указанных ниже функций.
а)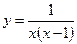 
.
▲ Т.к. знаменатель дроби, задающей функцию, не должен равняться нулю, то
.
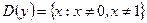б)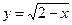 
.
▲ Т.к. функция задается при помощи корня чётной степени из выражения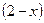 
, то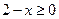 
и поэтому
.
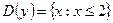2)Для указанных ниже функций определить, будет ли функция чётной, нечетной, функцией общего вида.
а) .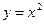
▲ Функция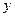 
– чётная, т.к. 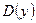симметрична относительно точки 
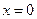и 
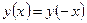для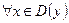 
.
б)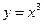 
.
▲ Функция 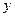– нечётная, т.к. 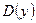симметрична относительно точки 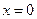и 
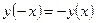для .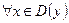
в)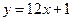 
.
▲ Функция 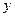не является ни четной, ни нечетной, т.к. 
: 
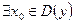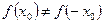и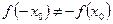 
. В качестве 
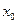можно взять, например, 
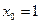. (Заметим, что симметрична относительно точки ).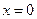
г)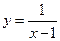 
.
▲ Функция 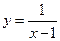не является ни четной, ни нечетной, т.к. 
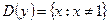не симметрична относительно точки .
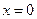3)Найти значение функции в заданной точке :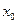
а)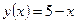 
, 
, ; 
.
▲ 
, 
.
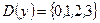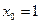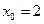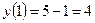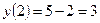б)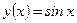 
, 
.
▲ 
.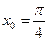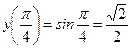