Понятие функции. Основные элементарные функции, их свойства и графики

Скворцова М.И., Мудракова О.А., Кротов Г.С.

Практикум

По математическому анализу

Для студентов вечернего отделения

Ого курса

(Часть I)

Учебно-методическое пособие

Москва, 2006

УДК 512.8:516

ББК С42

Рецензенты:

к.ф.-м.н., доцент Каролинская С.Н. (Московский авиационный институт им. С. Орджоникидзе);

к.ф.-м.н., доцент Краснослободцева Т.П. (МИТХТ им. М.В. Ломоносова).

Скворцова М.И., Мудракова О.А., Кротов Г.С. Практикум по математическому анализу для студентов вечернего отделения 1-го курса (Часть I). Учебно-методическое пособие – М.: МИТХТ им. М.В. Ломоносова, 2006 – 46 с.: ил. 29 .

Утверждено Библиотечно-издательской комиссией МИТХТ им. М.В. Ломоносова в качестве учебно-методического пособия. Поз. ___/2006.

Пособие представляет собой конспекты 6 практических занятий по курсу математического анализа для студентов вечернего отделения МИТХТ им. М.В. Ломоносова. В Часть I включены следующие разделы: "Функция и ее основные свойства", "Предел функции", "Непрерывность и точки разрыва функции".

Каждое занятие посвящено отдельной теме. Конспекты пяти занятий содержат краткое изложение соответствующей теории, типовые примеры и задачи для самостоятельного решения (с ответами). В конспекте занятия №6 приведен образец варианта контрольной работы (с решениями), проводимой на этом занятии.

Пособие предназначено для студентов вечернего отделения вузов химического профиля.

© МИТХТ им. М.В. Ломоносова, 2006

ОГЛАВЛЕНИЕ

Занятие 1.

Понятие функции. Основные элементарные функции, их свойства и графики ……………………….......

Занятие 2.Полярная система координат. Построение графиков функций методом сдвига и растяжения вдоль осей координат ………………………………………………………

Занятие 3.Предел функции. Непрерывность функции. Вычисление пределов непрерывных, рациональных и некоторых иррациональных функций …………................................

Занятие 4.Первый и второй замечательные пределы. Вычисление пределов степенно-показательной функции. Бесконечно малые и бесконечно большие
величины …………………………………………………….

Занятие 5.Точки непрерывности и точки разрыва функции. Классификация точек разрыва. Исследование функции на непрерывность ………………………………………………..

Занятие 6.Контрольная работа №1 по теме "Вычисление пределов функций. Исследование функции на непрерывность"…………………………………………………………

Литература…………………………………………………

Занятие 1.

Понятие функции. Основные элементарные функции, их свойства и графики.

Определение 1.Зависимость переменной 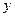от переменной 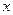называется функцией, если каждому значению 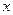соответствует единственное значение .

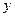Пишем: 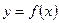и говорим, что 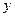есть функция от 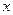. Переменная 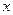называется независимой переменной (или аргументом), а 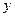– зависимой переменной.

Определение 2. Область определения функции 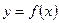(обозначаемая через 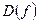) – это множество всех значений, которые принимает 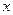. Множество значений функции (обозначаемое через 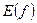) – это множество всех значений, которые принимает .

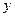Определение 3. Функция 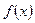называется возрастающей (убывающей) на числовом промежутке 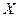, если для любых 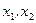из 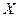таких, что 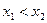, выполнено неравенство:

.

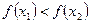
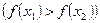Определение 4. Функция 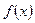называется монотонной на промежутке 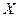, если она только убывает или только возрастает на .

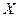Определение 5. Функция 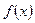называется четной (нечетной), если её 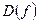симметрична относительно нуля и для любого х из 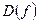выполнено равенство

.

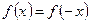
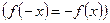Заметим, что 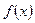может не являться четной и не являться нечетной. В этом случае говорят, что f(x) – функция общего вида.

Определение 6. Функция 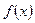называется периодической, если существует число 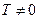, такое, что для любого 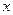из 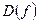точки 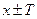также принадлежат 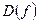и 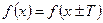. Любое такое число Т называется периодом функции; наименьший положительный период называется основным периодом функции.

Замечания.

1) Далее мы будем использовать следующие логические символы: $– "существует"; Î – "принадлежит"; " – "любой, всякий"; Þ – "следует"; Û – "тогда и только тогда";

2)далее будем использовать следующие обозначения: N – множество натуральных чисел, R – множество действительных чисел, Æ – пустое множество.