Основные свойства определителей

Определитель (детерминант) вводится только для квадратной матрицы и записывается в следующем виде:

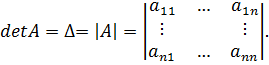
Порядок определителя матрицы равен числу её строк или столбцов.

Определитель – это число, равное сумме произведений элементов производной сроки (или столбца) матрицы на их алгебраические дополнения:

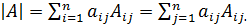(3.1)

Здесь 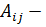алгебраическое дополнение элемента 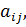которое вычисляется по выражению

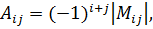(3.2)

где 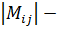минор, который является новым определителем и получается из исходного определителя вычёркиванием строки и столбца, содержащих элемент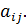

Используя соотношения (3.1) и (3.2), разложение определителя можно довести до миноров второго порядка, которое легко вычисляется по следующему правилу:

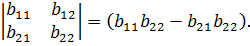
Пример 3.4. Разложение определителя третьего порядка по третьему столбцу:

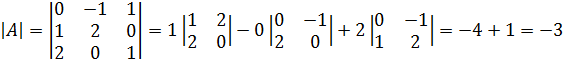
Для матриц высокого порядка вычисление детерминанты представляет довольно трудоёмкую процедуру. Поэтому в инженерной практике в настоящее время обычно используют для этой цели встроенную в MatLab функцию det().

Определители обладают рядом свойств:

1. Значение определителя не изменится, если его строки (столбцы) поменять местами с соответствующими столбцами (строками), т.е. имеем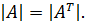

2. Знак определителя изменится на противоположный при перестановке местами двух столбцов или строк.

3. Если в определителе одна из строк (столбцов) является нулевой, то значение определителя равно нулю.

4. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

5. Если элементы какой-либо строки (столбца) определителя имеют одинаковый множитель, то его можно вынести за знак определителя.

6. Если к какой-либо строке (столбцу) определителя прибавить другую его строку (столбец), умноженную на некоторое число, то значение определителя не изменится.

7. Если все элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.

8. Если элементы некоторой k-ой строки определителя являются суммами двух слагаемых, то определитель можно разложить сумму двух определителей в следующем виде:

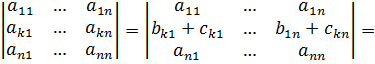
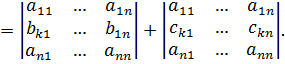
Это свойство позволяет разбивать определитель на несколько частных определителей с целью упрощения вычисления исходного определителя.

Можно привести ещё ряд полезных операций над определителями:

· определитель произведения матриц AB равен произведению определителей этих матриц: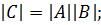

· производная по элементу 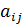равна алгебраическому дополнению 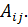Это следует из (3.1):

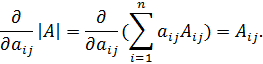
Обращение матрицы

Обратная матрица 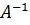удовлетворяет условию: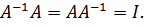

Её получение является одним из основных моментов при решении матричных уравнений. Пусть, например, дано уравнение

Ax = b, (3.3)

где x – вектор вычисляемых координат; b – вектор-столбец вещественных чисел.

Решение получается умножением слева уравнения (3.3) на обратную (инверсную) матрицу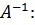

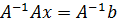
или, учитывая, что 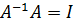имеем

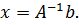(3.4)

Обратная матрица находится по выражению

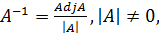(3.5)

где 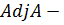присоединённая матрица, образованная из алгебраических дополнений 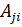(3.2):

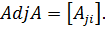(3.6)

Из (3.6) следует, что присоединённая матрица является транспонированной для матрицы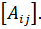

Пример 3.5. Определить обратную матрицу для заданной матрицы А:

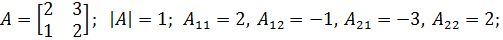
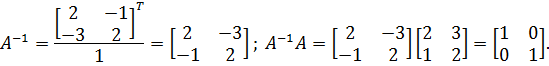
Следует отметить, что для матриц высокого порядка операция обращения весьма затруднительна. Поэтому для решения этой задачи в настоящее время используют машинные методы вычисления обратных матриц. В частности, в среду MatLab для этой цели встроена функция inv().

Единственным требованием для возможности выполнения операции обращения матрицы является условие невырожденности матрицы, которое следует из (3.5):

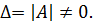(3.7)

Для проверки этого условия осуществляют вычисление так называемого ранга матрицы A. Ранг равен наибольшему числу линейно независимых строк (или столбцов). Определяется ранг по минорам: если какой-либо минор порядка r матрицы A не равен нулю, а все миноры, начиная с порядка r+1, равны нулю, то число r называется рангом матрицы:

r = rang A.

Очевидно, что ранг квадратной матрицы, определитель который не равен нулю, равен её размеру, т.е. r = n.

Вычисление ранга также довольно трудоёмкая процедура, поэтому для оценки невырожденности матрицы используют в настоящее время программные продукты. В частности, в MatLab для решения этой задачи применяется функция rank(), результат выполнения которой затем сравнивается с порядком n матрицы A с целью проверки условия r = n.

Представляет также интерес операция обращения произведения матриц. Она подобна рассмотренной выше операции транспонирования произведения двух матриц.

Пусть C = AB, тогда умножив слева это равенство на 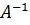получим 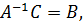далее аналогично 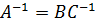и соответственно 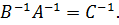Таким образом, имеем

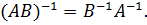(3.8)

Это соотношение часто используется в математических преобразованиях при получении матричных моделей и ??? в современной теории управления, которая базируется на применении матричных методов анализа и синтеза автоматических систем.