Частотные критерии устойчивости
Для оценки устойчивости замкнутой системы при известной ее АФЧХ используют частотный критерий Найквиста — Михайлова. Необходимая АФЧХ разомкнутой системы может быть получена следующим образом.
Если имеется передаточная функция разомкнутой системы 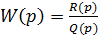 , гдеR(p)и Q(p)— полиномы от р то, заменив р на
, гдеR(p)и Q(p)— полиномы от р то, заменив р на 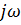 , получим уравнение АФЧХ разомкнутой системы
, получим уравнение АФЧХ разомкнутой системы 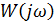 . Чтобы построить АФЧХ, необходимо представить ее состоящей из вещественной и мнимой частей:
. Чтобы построить АФЧХ, необходимо представить ее состоящей из вещественной и мнимой частей:
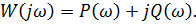
Затем, задаваясь значениями 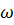 от 0 до
от 0 до 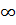 :
: 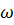 =0;
=0; 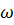 =
= 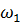 ;
; 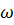 =
= 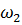 и т.д., необходимо найти точки
и т.д., необходимо найти точки 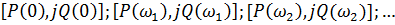 и по ним построить АФЧХ на комплексной плоскости (рис. 7, а).
и по ним построить АФЧХ на комплексной плоскости (рис. 7, а).
Рис.7. АФЧХ устойчивой (а) и находящейся на границе устойчивости (б) разомкнутых систем, которые будут устойчивыми в замкнутом состоянии.
Рис.8. АФЧХ неустойчивой разомкнутой системы (m=1), которая будет устойчивой в замкнутом состоянии.
Рассмотрим основные свойства АФЧХ разомкнутой системы. Если разом кнутая система не имеет интегрирующих звеньев, то при 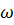 = 0 ее АФЧХ начинается на вещественной оси в точке
= 0 ее АФЧХ начинается на вещественной оси в точке  —коэффициент усиления разомкнутой системы. Заканчивается АФЧХ при
—коэффициент усиления разомкнутой системы. Заканчивается АФЧХ при  =
=  в начале координат (рис. 7,а). Если разомкнутая система имеет одно интегрирующее звено, то ее АФЧХ начинается при
в начале координат (рис. 7,а). Если разомкнутая система имеет одно интегрирующее звено, то ее АФЧХ начинается при 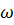 =
= 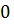 в бесконечности на отрицательной мнимой полуоси и заканчивается в начале координат (рис.7, б).
в бесконечности на отрицательной мнимой полуоси и заканчивается в начале координат (рис.7, б).
Важно отметить, что разомкнутая система может быть устойчивой, неустойчивой или находиться на границе устойчивости. Если система состоит только из устойчивых элементов, то она будет устойчивой в разомкнутом состоянии. При наличии хотя бы одного неустойчивого элемента она будет неустойчивой. При наличии одного интегрирующего звена разомкнутая система находится на границе устойчивости (в литературе такие системы иногда называют нейтрально- устойчивыми).
Сформулируем теперь критерий Найквиста — Михайлова:
если разомкнутая система устойчива или находится на границе устойчивости, то для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении 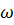 от 0 до
от 0 до 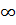 не охватьвала точку с координатами — 1, j0. Если разомкнутая система неустойчива, а ее передаточная функция имеет т полюсов справа от мнимой оси плоскости р, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении
не охватьвала точку с координатами — 1, j0. Если разомкнутая система неустойчива, а ее передаточная функция имеет т полюсов справа от мнимой оси плоскости р, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении 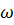 от —
от — 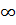 до +
до + 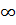 охватьвала точку — 1, j0т раз.
охватьвала точку — 1, j0т раз.
Как определить, охватывает ли АФЧХ разомкнутой системи точку—1, j0, если разомкнутая система находится на границе устойчивости? Ведь АФЧХ при 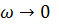 уходит в бесконечность. В этом случае мысленно соединяют конец АФЧХ при
уходит в бесконечность. В этом случае мысленно соединяют конец АФЧХ при 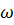 =
= 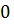 с положительной вещественной полуосью дугой окружности бес- конечно большого радиуса (рис. 7,б). Тогда можно однозначно определить, охватывает ли АФЧХ точку — 1, j0.
с положительной вещественной полуосью дугой окружности бес- конечно большого радиуса (рис. 7,б). Тогда можно однозначно определить, охватывает ли АФЧХ точку — 1, j0.
Почему в случае устойчивости разомкнутой системы рассматривается АФЧХ при изменении 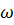 от 0 до
от 0 до 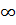 , а в случае неустойчивой — при изменении
, а в случае неустойчивой — при изменении 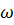 от —
от — 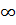 до +
до + 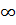 ? На практике АФЧХ может быть снята только для положительных частот (0
? На практике АФЧХ может быть снята только для положительных частот (0 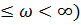 . С математической точки зрения АФЧХ должны строиться для всего диапазона частот —
. С математической точки зрения АФЧХ должны строиться для всего диапазона частот — 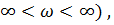 при этом ветвь АФЧХ для отрицательных частот симметрична относительно вещественной оси ветви, построенной для положительных частот. Если эта ветвь не охватывает или охватывает точку —1, j0, то учет первой ветви с отрицательными частотами ничего не изменит.
при этом ветвь АФЧХ для отрицательных частот симметрична относительно вещественной оси ветви, построенной для положительных частот. Если эта ветвь не охватывает или охватывает точку —1, j0, то учет первой ветви с отрицательными частотами ничего не изменит.
Если же разомкнутая система неустойчива, то для устойчивости замкнутой системы требуется, чтобы АФЧХ разомкнутой системы (при 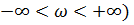 охватывала точку
охватывала точку 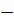 1, j0т раз. Если же рассматривать только положительную ветвь, то она должна охватывать эту точку
1, j0т раз. Если же рассматривать только положительную ветвь, то она должна охватывать эту точку 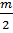 раз.
раз.
Например, при m=1 она должна охватывать ее 1/2 раза. Однако такое определение довольно неудачное. Поэтому при неустойчивой разомкнутой системе рассматривают обе ветви ее АФЧХ, т. е. берут диапазон изменения частота от 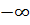 до
до 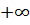 (рис. 8). Отсюда видно, что при использовании частотного критерия устойчивости определяющим является положение АФЧХ разомкнутой системы вблизи точки — 1, j0.
(рис. 8). Отсюда видно, что при использовании частотного критерия устойчивости определяющим является положение АФЧХ разомкнутой системы вблизи точки — 1, j0.
С помощью критерия Найквиста — Михайлова, как и по критерию устойчивости Михайлова, можно оценивать влияние параметров элементов системы на ее устойчивость. Для этого необходимо построить АФЧХ разомкнутой системы при данном значении интересующего нас параметра и определить устойчивость замкнутой системы. Пусть для примера система оказалась устойчивой (рис. 9). Изменим значение этого параметра. Пусть при новом значении параметра (например, при большем) АФЧХ приняла вид, изображенный на рис.9 пунктиром. Следовательно, увеличение интересующего нас параметра способствует неустойчивости системы.
Рис.9. АФЧХ устойчивой разомкнутой системы.
Так как критерий Найквиста — Михайлова использует экспериментально снять АФЧХ, то нетрудно дать его физическую трактовку. Поясним это вначале на примере системы, находящейся на границе устойчивости. В этом случае АФЧХ разомкнутой системы при некоторой частоте 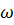 с проходит через точку — 1, j0 (рис. 9). Это означает, что при данной частоте
с проходит через точку — 1, j0 (рис. 9). Это означает, что при данной частоте 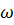 с амплитуда выходного сигнала равна амплитуде входного сигнала, а его фаза прямо противоположна фазе входного сигнала, т. е. сдвиг по фазе между ними равен —
с амплитуда выходного сигнала равна амплитуде входного сигнала, а его фаза прямо противоположна фазе входного сигнала, т. е. сдвиг по фазе между ними равен — 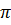 . При замыкании системы основная обратная связь должна быть отрицательной, т. е. фазу выходного сигнала при подаче его на вход системы следует повернуть на
. При замыкании системы основная обратная связь должна быть отрицательной, т. е. фазу выходного сигнала при подаче его на вход системы следует повернуть на 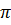 . Кроме того, при этом следует отключить внешний источник колебаний, который подавал гармонические сигналы на вход системы.
. Кроме того, при этом следует отключить внешний источник колебаний, который подавал гармонические сигналы на вход системы.
Таким образом, при замыкании системы выходной сигнал (правда, теперь он уже не будет выходным, так как он подан на вход системы, но мы по-прежнему для ясности будем его называть выходным) будет совпадать по амплитуде и фазе со входным сигналом, т. е. при замыкании системы в ней ничего не изменится. В системе установятся незатухающие колебания, причем они будут поддерживаться не за счет энергии источника входного сигнала (он теперь отключен), а за счет энергии самой системы. Это и означает нахождение системы на границе устойчивости.
Если АФЧХ при частоте 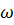 с пересекает вещественную ось слева от точки — 1, j0, то она охватывает данную точку. Это говорит о том, что в разомкнутой системе амплитуда выходного сигнала на данной частоте
с пересекает вещественную ось слева от точки — 1, j0, то она охватывает данную точку. Это говорит о том, что в разомкнутой системе амплитуда выходного сигнала на данной частоте 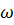 с больше амплитуды входного сигнала, а сдвиг по фазе между ними равен —
с больше амплитуды входного сигнала, а сдвиг по фазе между ними равен — 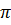 . При замыкании системы и отключении источника внешних колебаний амплитуда выходных колебаний будет возрастать, т. е. система будет неустойчивой.
. При замыкании системы и отключении источника внешних колебаний амплитуда выходных колебаний будет возрастать, т. е. система будет неустойчивой.
Если АФЧХ не охватывает точки — 1, j0, то при сдвиге по фазе, фавном — 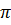 , амплитуда выходного сигнала меньше амплитуды входного сигнала. В этом случае при замыкании системы колебания в ней будут затухать, т. е. система будет устойчивой.
, амплитуда выходного сигнала меньше амплитуды входного сигнала. В этом случае при замыкании системы колебания в ней будут затухать, т. е. система будет устойчивой.
Теперь рассмотрим, как применить частотный критерий устойчивости Найквиста — Михайлова, если в распоряжении имеется не АФЧХ, а ЛАЧХ разомкнутой системы. Сформулируем этот критерий для данного случая.
Замкнутая минимально-фазовая * система устойчива, если при достижении фазовой частотной характеристики, значения — 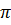 логарифмическая амплитудно-частотная характеристика будет отрицательной (рис. 10).
логарифмическая амплитудно-частотная характеристика будет отрицательной (рис. 10).
Рис. 10. ЛАЧХ нейтральной (а) и неустойчивой (б) разомкнутых систем в замкнутом состоянии.
Почему рассматривается ЛАЧХ при значении фаз в, равном — 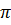 ? Потому что устойчивость согласно критерию Найквиста — Михайлова оценивается по тому, с какой сторони от точки— 1, j0 АФЧХ пересекает вещественную ось комплексной плоскости, а при пересечении вещественной оси фаза АФЧХ равна —
? Потому что устойчивость согласно критерию Найквиста — Михайлова оценивается по тому, с какой сторони от точки— 1, j0 АФЧХ пересекает вещественную ось комплексной плоскости, а при пересечении вещественной оси фаза АФЧХ равна — 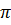 .
.
Если ЛАЧХ отрицательна, то модуль АФЧХ меньше единицы, поскольку числа, меньшие единицы, имеют отрицательный логарифм. Отрицательность ЛАЧХ при фазе — 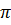 говорит о том, что АФЧХ разомкнутой системи не охватывает точку — 1, j0.
говорит о том, что АФЧХ разомкнутой системи не охватывает точку — 1, j0.
Почему при оценке устойчивости системы по ЛАЧХ оговаривается, что критерий Найквиста — Михайлова применим только для минимально-фазовых систем? Ведь при использовании АФЧХ такого ограничения не было. Это объясняется тем, что при оценке устойчивости по ЛАЧХ рассматривается только часть ее при фазе, близкой к — 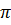 , или часть АФЧХ в окрестности пересечения ею вещественной оси.
, или часть АФЧХ в окрестности пересечения ею вещественной оси.
Только для минимально-фазовых систем рассмотрение части АФЧХ (ЛАЧХ) позволяет судить о всей характеристике. Для неминимально-фазовых систем этого сделать нельзя.
Все рассмотренные критерии устойчивости тем или иным способом оценивают один и тот же факт: имеются ли среди корней характеристического уравнения замкнутой системы корни с положительной вещественной частью. Поэтому все они дают одинаковый результат в оценке устойчивости системы.
Отметим, что во всех случаях раньше, чем исследовать устойчивость с помощью того или иного критерия, следует убедиться, что необходимое условие устойчивости выполняется, т. е. все коэффициенты характеристического уравнения системы являются положительными числами.
