Математическая модель позиционирования и координирования с помощью GPS

Основные теоретические положения GPS-метода

Геометрическая основа относительного позиционирования

Первые разности

Относительное позиционирование заключается в определении приращений координат в пространственной системе координат между точками земной поверхности. При этом положение спутников считается известным и от них измеряются дальности к точкам земной поверхности – приемникам.

Определение приращений координат базируется на разностях измеренных дальностей. При измерении двух дальностей D₁ и D₂ от одного спутника к двум приемникам 1 и 2.(рис.1.1)

D₁ D₃ D₂ D₄

1 2

Рис.1.1

Можно записать два уравнения

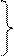D₁²=(X₁-X_s)²+(Y₁-Y_s)²+(Z₁-Z_s)² (1.1)

D₂²=(X₂-X_s)²+(Y₂-Y_s)²+(Z₂-Z_s)²

Поскольку будут определяться приращения координат, то запишем

X₂= X₁+∆X

Y₂= Y₁+∆Y (1. 2)

Z₂= Z₁+∆Z

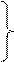После подстановки (1.2) во второе уравнение системы (1.1) запишем

D₁²=(X₁-X_s)²+(Y₁-Y_s)²+(Z₁-Z_s)² (1.3)

D₂²=(X₁-X_s+∆X)²+(Y₁-Y_s+∆Y)²+(Z₁-Z_s+∆Z)²

Раскрывая скобки во втором уравнении (1.3) эту систему перепишем так

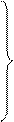D₁²=(X₁-X_s)²+(Y₁-Y_s)²+(Z₁-Z_s)²

D₂²=(X₁-X_s)²+2∆X(X₁-X_s)+∆X²+ (1.4)

+(Y₁-Y_s)²+2∆Y(Y₁-Y_s)+ ∆Y²+

+(Z₁-Z_s)²+2∆ Z (Z ₁- Z _s)+ ∆ Z ²

Разность уравнений (1.4) составляет

D₂²-D₁²=2∆X(X₁-X_s)+∆X²+2∆Y(Y₁-Y_s)+∆Y²+2∆ Z (Z ₁- Z _s)+ ∆ Z ² (1.5)

На основе (1.5) можно составить следующее уравнение относительно ∆x, ∆y, ∆z.

(X₁-X_s) ∆X+ (Y₁-Y_s) ∆Y +(Z ₁- Z _s) ∆ Z+L=0 (1.6)

Где L= ½((∆X²+∆Y²+∆ Z²-( D₂²- D₁²))

Однако в (1.6) неизвестные величины ∆x, ∆y, ∆z присутствуют в свободном члене L. Кроме того, неизвестными являются и координаты X₁, Y₁, Z_1. Таким образом, в данном уравнении шесть неизвестных. Для его решения необходимо составление еще пять таких уравнений. Однако в конечном итоге необходимо четыре. Определить лишь ∆x, ∆y, ∆z. То есть только при неизвестных. Для этого по четырем спутникам составляется четыре уравнения вида (1.6) и по ним – соответствующие разности, так называемые вторые разности. Эти вторые разности приводим к системе трех уравнений с тремя неизвестными.

Вторые разности

Система уравнений вида (1.6), составленная на основе четырех спутников имеет следующий вид

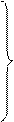(X₁-X_s1) ∆X+ (Y₁-Y_s1) ∆Y +(Z ₁- Z _s1) ∆Z+L₁=0

(X₁-X_s2) ∆X+ (Y₁-Y_s2) ∆Y +(Z ₁- Z _s2) ∆Z+L₂=0 (1.7)

(X₁-X_s3) ∆X+ (Y₁-Y_s3) ∆Y +(Z ₁- Z _s3) ∆Z+L₃=0

(X₁-X_s4) ∆X+ (Y₁-Y_s4) ∆Y +(Z ₁- Z _s4) ∆Z+L₄=0

Где

S₂

S₁ S₃

D₂

D₁

D₃ D₄ S₄

D₇ D₈

D₅ D₆

1 2

Рис.1.2

L₁= ½((∆X²+∆Y²+∆ Z²-( D₂²- D₁²))

L₂= ½((∆X²+∆Y²+∆ Z²-( D₄²- D₃²)) (1.8)

L₃= ½((∆X²+∆Y²+∆ Z²-( D₆²- D₅²))

L₄= ½((∆X²+∆Y²+∆ Z²-( D₈²- D₇²))

Во всех уравнениях присутствует общий член:

X₁∆X + Y₁∆Y+Z ₁∆Z- ½ (∆X²+∆Y²+∆ Z²)

Его можно исключить, составляя независимые разности этих уравнений. Точных разностей будет три. Их лучше составить относительно первого уравнения системы (1.7). Так разность первого и второго уравнений приводит к выражению

(X_s2- X_s1)∆X+(Y_s2- Y_s1)∆Y+(Z_s2- Z_s1)∆Z+ L₁₂=0 (1.9)

Где

L₁₂=½((D₄²- D₃²)-(D₂²- D₁²))

Таким образом, может быть получена следующая система уравнений.

(X_s2- X_s1)∆X+(Y_s2- Y_s1)∆Y+(Z_s2- Z_s1)∆Z+ L₁₂=0

(X_s3- X_s1)∆X+(Y_s3- Y_s1)∆Y+(Z_s3- Z_s1)∆Z+ L₁₃=0 (1.10)

(X_s4- X_s1)∆X+(Y_s4- Y_s1)∆Y+(Z_s4- Z_s1)∆Z+ L₁₄=0

Где

L₁₃=½((D₆²- D₅²)-(D₂²- D₁²))

L₁₄=½((D₈²- D₇²)-(D₂²- D₁²))

В матричной форме систему (1.10) можно записать так

AX+L=0 (1.11)

Где

X_s2- X_s1 Y_s2- Y_s1 Z_s2- Z_s1

A= X_s3- X_s1 Y_s3- Y_s1 Z_s3- Z_s1 (1.12)

X_s4- X_s1 Y_s4- Y_s1 Z_s4- Z_s1

L₁₂ ∆X

L= L₁₃ X= ∆Y

L₁₄ ∆Z

Из (1.11) находим вектор приращений координат

X=-A^-1L (1.13)

Оценку точности решения можно произвести по формуле

K_X=A^-1K_L(A^-1)^T (1.14)

где

K_L и K_X –корреляционные матрицы векторов сводных членов и неизвестных – приращений координат.

Диагональные элементы матрицы K_L- суть дисперсии составляющих вектора L. Так, полагая измерения дальностей независимыми величинами можно записать, что

m²_D1=4D²m²_D (1.15)

Ковариационный момент составляющих вектора L будет равен

kov=2D²m²_D

Тогда матрица K_L будет

2 1 1

K_L=2D² 1 2 1 m²_L (1.16)

1 1 2

где

m²_L – средняя квадратическая ошибка.

Для упрощения выводов по оценки точности расположим точки S₁, S₂, S₃, S₄ таким методом (рис.1.3), чтобы матрица приняла вид

Z

S₄

S₃ Y

S₁

S₂

X 2

1

Рис.1.3

X_s2- X_s1 0 0

A= 0 Y_s3- Y_s1 0 (1.17)

0 0 Z_s4- Z_s1

Обратной ей будет матрица

1/ X_s2- X_s1 0 0

A^-1= 0 1/ Y_s3- Y _s1 0 (1.18)

0 0 1/Z_s4- Z_s1

Полагая

X_s2- X_s1 =В₁

Y_s3-Y_s1 = В₂ (1.19)

Z_s4 - Z_s1=В₃

Найдем

2/B₁ 1/B₁ 1/B₁

A^-1 K_L= m²_D2D² 1/B₂ 2/B₂ 1/B₂ (1.20)

1/B₃ 1/B₃ 2/B₃

и соответственно

2/B₁² 1/B₁ B₂ 1/B₁B₃

K_x= m²_D2D² 1/B₁ B₂ 2/B₂² 1/B₂B₃ (1.21)

1/B₁B₃ 1/B₂B₃ 2/B₃²

Таким образом средняя квадратическая ошибка измерения приращения координат по любой оси будет.

A= 2m²_D1/B (1.22)

Корреляционный момент между этими величинами составит.

K_A=√2m²_DD²/B² (1.23)

Коэффициент корреляции можно найти так

R=K/m_xm_y (1.24)

Что составляет величину

R=0,5

Различают "однобазовое" и "многобазовое" определения, причем последний термин применяют, если число пунктов превышает два. При статической съемке достижима относительная точность от 10^-6 до 10^-7, что эквивалентно миллиметровой точности для баз длиной до нескольких километров.

Кинематическое относительное определение положения выполняется по одновременным наблюдениям на одном неподвижном и одном движущемся приемниках. Метод применяется там же, где и кинематическое абсолютное определение положения, но достигается более высокая точность. Точность в дифференциальном (по кодовым дальностям) определении находится на метровом уровне, а в относительном (по фазам несущей) методе достижима сантиметровая точность.

"Полукинематический" метод, или метод "остановки и движения" (Stop and Go), является комбинацией статического и кинематического относительных определений положения. В этом методе движение приемника чередуется с остановками в заданных пунктах. Наблюдения ведутся постоянно, но во время остановок накапливаются эпохи измерений и, соответственно, повышается точность определений. Метод часто называют просто "кинематической съемкой".

"Псевдокинематический" или "прерывистый статический" метод определения положения предполагает, что на интересующих пунктах наблюдения выполняют еще один раз (примерно через час после первого посещения пункта). Это делается для того, чтобы облегчить разрешение неоднозначности и получить более высокую точность. В основном эти цели достигаются вследствие изменения конфигурации сети спутников. При этом не требуется поддержания непрерывности сигнала между посещениями станции, и приемник во время движения можно даже отключать.

"Быстростатические" методы используют комбинации псевдодальностей и фаз несущей с целью выполнить быструю инициализацию (то есть разрешить неоднозначность) в статическом режиме. В этом случае требуются измерения как кода, так и фазы несущей, на обеих частотах. Наблюдения в течение 5-10 минут могут дать относительную точность 10^-6.

"Безостановочные (On-The-Fly)" методы позволяют выполнить инициализацию в кинематическом режиме, а не в статическом. Этот метод с использованием кодовых данных позволяет определять положения движущихся объектов с дециметровой и даже с сантиметровой точностью, если неоднозначности разрешены.

Выбор метода GPS съемки зависит от требований проекта, главным образом, к точности определения положений. При использовании одного приемника имеет смысл лишь определение координат одного пункта - "абсолютное определение положения" пункта. При этом не следует забывать, что неограниченный доступ возможен лишь к коду С/А, и что точность может быть искусственно ухудшена включением режима выборочного доступа (SA - Selective Availability). Более точный Р-код в случае режима антиимитации (AS - Anti-Spoofing) или засекречивания Р-кода доступен лишь пользователям, имеющим на это разрешение.

При использовании двух или большего числа приемников, один из пунктов служит корректирующей станцией, и на втором пункте достижимы высокие точности. В дифференциальном режиме наблюдаются кодовые псевдодальности одновременно до четырех (обычно) или более спутников. Корректирующая станция вычисляет действительные поправки к наблюдаемым кодовым псевдодальностям. Эти поправки затем передаются средствами связи на неизвестные пункты, приводя к уточнению независимо вычисленных положений. Поскольку Р-кодовые приемники обеспечивают точность кодовых дальностей на метровом уровне с помощью дифференциального метода достижима субметровая точность определения положения. Следовательно, можно строить сети ниже третьего класса. Преимуществом метода кодовой псевдодальности является его нечувствительность к скачкам фазы и, до некоторой степени, к препятствиям около пункта. Значит, в лесных районах деревья оказывают на кодовые наблюдения меньше влияния, чем на измерения фазы несущей.

В настоящее время геодезические точности достижимы лишь при использовании измерений фаз несущей, выполненных в режиме относительного определения положений. Обработка вектора базы требует, чтобы фазы наблюдались одновременно на обоих концах базы. Следовательно, относительное определение положения было раньше возможно лишь в последующей обработке наблюдений. Недавно были сделаны успешные попытки передачи результатов наблюдений на коротких базах в реальном времени, что дало возможность в реальном времени вычислять вектор базы (Hoffmann-Welenhof et al, 1990).

Метод статической съемки является наиболее используемым, поскольку единственным основным требованием является относительное отсутствие препятствий для обзора неба на пунктах. Обычно для статической съемки нужно 60-120 минут наблюдений. Однако, этот метод включает в себя использующий более короткие интервалы наблюдений (например, 10 минут) метод "широкой полосы (wide- line)" или метод быстростатической съемки, основанный на быстром разрешении неоднозначности (Frei, Beutler, 1990). Для длинных баз ( > 50 км) обнаружение скачков фаз и разрешение неоднозначностей усложняется. В таких случаях может быть полезным использование дополнительных приемников в окрестностях обоих пунктов базы. Неоднозначности определяются для коротких баз и затем используются для определения неоднозначностей на длинных базах. Эта процедура называется "добавочным расширением (boot- strapping)" сети (Stangle et al,1991). Обычно статическая съемка используется при государственных, областных и местных контрольных съемках, при фотоконтрольных съемках, при исследовании деформаций и границ плит.

Метод кинематической съемки является наиболее производительным в том смысле, что за наименьшее время можно определить положения наибольшего числа пунктов. Тогда как в статическом методе GPS требуется, чтобы спутники перемещались по небу, в кинематическом методе этого не требуется. Поэтому для кинематического метода является полезным предлагаемое совместное с GPS использование геостационарных спутников. Кинематическая съемка требует проведения тщательной рекогносцировки на местности, поскольку не только пункты остановок и неподвижные пункты, но и трасса между пунктами, по которой движется приемник, должны быть свободны от препятствий. Кинематический метод требует непрерывного сигнала от четырех или более спутников в течение всей съемки. На практике это означает, что движущийся приемник не может проезжать под деревом или близко к столбу. Метод наиболее подходит широким открытым местностям с малым количеством препятствии, а также и для пригородов, где не слишком много больших деревьев нависает над дорогой. С помощью этого метода можно определять положение приемника, размещенного на наземном транспорте, движущемся по данному району по пересекающимся линиям. Трехмерные координаты этого приемника можно определить с высокой точностью (несколько сантиметров), так что возможно подготовить точную топографическую карту этого района.

Псевдокинематическая съемка наиболее близка к статическому методу. Такая съемка требует меньшего времени нахождения приемника в пункте, но нужно дважды побывать на обоих пунктах базы. Обычная схема наблюдений такова: пребывание на обоих пунктах в течение пяти минут, переезд к другим пунктам, и, через один час после первого посещения первой пары пунктов, возврат к ней для повторного наблюдения в течение пяти минут. Преимуществом этого 10-минутного (в сумме) интервала наблюдений, в отличии от 60-минутного, является наличие некоторого промежутка времени, потерянного на переезд к пунктам для повторного наблюдения.

Псевдокинематический метод оптимален для ситуации когда пункты находятся вдоль дороги, по которой наблюдатели могут быстро двигаться в промежутках между наблюдениями на пунктах. Главным преимуществом метода является то, что за заданный интервал времени можно побывать на большем числе пунктов, чем при использования обычного статического метода. В сравнении с кинематическим методом, допускается потеря сигнала, а число спутников не играет такой существенной роли. Слабой стороной метода является необходимость возвращения на пункты. Это ограничивает метод лишь локальными его применениями. Главным конкурентом метода является быстростатический метод определения положений, в котором нет необходимости вновь посещать пункты. Псевдокинематический метод используется для съемки фотосети контрольных пунктов, для съемок контрольных пунктов низкого порядка, для съемок территорий шахт.

На практике лучше использовать комбинации этих трех методов. Например, статический и псевдокинематический методы можно использовать для установления широкой структуры сети контрольных пунктов и для установки пунктов на другой стороне препятствий, таких, как мосты. Кинематическую съемку можно применить для определения координат большой части пунктов, используя статические пункты в качестве контрольных и для проверки качества наблюдений. Для таких смешанных пунктов необходима тщательная рекогносцировка.

Для того, чтобы иметь опорную сеть для последующих съемок и дать возможность преобразования GPS результатов к национальной системе координат, используют два типа контрольных GPS сетей: пассивные контрольные сети и активные контрольные сети. Пассивная сеть привязана к существующим триангуляционным монументам и высотным реперам. Недостатком такой сети является требование выполнения наблюдений на многих пунктах и поддержка этих пунктов. Однако эта система подходит, когда имеются густые национальные триангуляционные сети и когда контрольная сеть служит другим целям, как, например, геодинамическим исследованиям. Такая густая пассивная контрольная сеть создана, например, в Австрии.

Целями активной контрольной сети являются вычисление и распространение в (почти) реальном времени дифференциальных поправок для пользователей, имеющих лишь один приемник, а также вычисление точных эфемерид в процессе постобработки (в офисе). Сбор и распространение данных выполняется с помощью высокоскоростных наземных, а также спутниковых систем связи.

Математическая модель позиционирования и координирования с помощью GPS