Методы прямоугольников

Министерство образования и науки РФ

ФГБОУ ВПО «Кубанский государственный технологический

Университет»

Кафедра электротехники и электрических машин

УТВЕРЖДАЮ
Заведующий кафедрой электротехники и электрических машин
к.т.н., доцент		ЯЯ.М. Кашин
____ _______ 2015 г.

Конспект лекций

По дисциплине «Численные методы расчета

Электрооборудования»

для студентов направления 13.04.02 «Электроэнергетика и электротехника»

Квалификация выпускника – магистр

Разработал:

к.т.н., доц. И.Н. Автайкин

Обсужден на заседании кафедры

электротехники и электрических машин

25 августа 2015 г. (протокол № 1)

Секретарь кафедры

к.т.н., доц. С.А. Попов

2015 г.

Лекция № 2(2 часа)

По дисциплине «Численные методы расчета электрооборудования»

Тема № 1. Численное интегрирование

Цели: 1. Формирование следующих компетенций:

ПК_Д-3 Способностью к освоению и применению современных средств анализа и моделирования работы электрооборудования.

2. Формирование уровня обученности:

Знать: современных средств анализа и моделирования работы электрооборудования.

Уметь: применять современные методы решения математических задач с использованием компьютерной техники.

Владеть: современным математическим аппаратом позволяющим анализировать математические модели электрооборудования.

Материальное обеспечение:

Учебные вопросы

1. Методы прямоугольников.

2. Метод трапеций.

3. Метод парабол (метод Симпсона).

Литература

1. Бахвалов Н.С., Жидков Н.П. Кобельков Г.М. Численные методы / Учебн. пособие- М.: Наука, 2011.- 631с.

2. Марчук Г.И. Методы вычислительной математики / Учебн. пособие- М.: Наука, 2011.- 535с.

Численное интегрирование

Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.

Численное интегрирование применяется, когда:

1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, .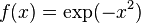

3. В этих двух случаях невозможно вычисление интеграла по формуле Ньютона — Лейбница

.

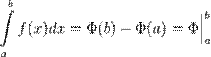Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.

Методы прямоугольников

Если же неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой Ньютона-Лейбница или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников (правых, левых, средних). При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)>=0 на отрезке [a; b], то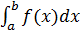

Разделим отрезок 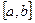на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка

Точки деления будут: x₀=a; x₁=a+h; x₂=a+2*h, ... , x_n-1=a+(n-1)*h; x_n=b.

Числа y₀, y₁, y₂, ... , y_n являются ординатами точек графика функции, соответствующих абсциссам x₀, x₁, x₂, ... , x_n (рис. 1.2).

Строим прямоугольники. Это можно делать несколькими способами:

Левые прямоугольники (слева на право)	Правые прямоугольники (построение справа на лево)

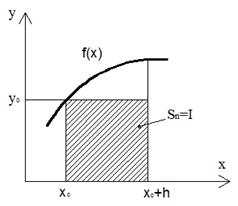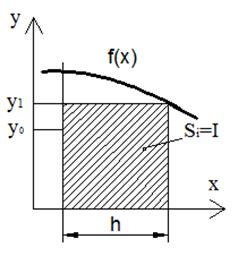Рис1 Рис 2