Проверка статистических гипотез
12/1 При заданном уровне значимости 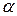 проверяется нулевая гипотеза
проверяется нулевая гипотеза 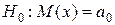 . Тогда конкурирующей может быть гипотеза…
. Тогда конкурирующей может быть гипотеза…
12/2При заданном уровне значимости 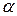 проверяется нулевая гипотеза
проверяется нулевая гипотеза 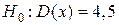 о равенстве дисперсии D(x) нормальной генеральной совокупности гипотетическому значению
о равенстве дисперсии D(x) нормальной генеральной совокупности гипотетическому значению 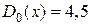 . Тогда конкурирующей может быть гипотеза
. Тогда конкурирующей может быть гипотеза
1) 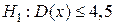 ; 2)
; 2) 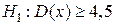 ; 3)
; 3) 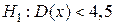 ; 4)
; 4) 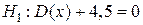 ;
;
12/3 При заданном уровне значимости 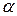 проверяется нулевая гипотеза
проверяется нулевая гипотеза 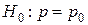 о равенстве неизвестной вероятности р гипотетическому значению
о равенстве неизвестной вероятности р гипотетическому значению 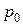 . Тогда конкурирующей может быть гипотеза…
. Тогда конкурирующей может быть гипотеза…
1) 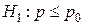 ; 2)
; 2) 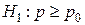 ; 3)
; 3) 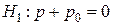 ; 4)
; 4) 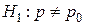 ;
;
Блок В
Основные понятия и теоремы теории вероятностей.
13/1 В партии из 12 деталей имеется 8 бракованные. Наудачу отобраны четыре. Тогда вероятность того, что среди отобранных деталей будут 2 бракованные, равна …
13/2. В среднем 80% студентов группы сдают зачет с первого раза. Тогда вероятность того, что из 6 человек, сдавших зачет, с первого раза сдадут равно 4 студента..
13/3Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательство первый станок 0,1; второй – 0,15; третий- 0,2. Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна…
1) 0,1 2) 0,329 3) 0,003 4) 0,45
13/4В первой урне 7 белых и 3 черных шара. Во второй урне 4 белых и 5 черных. Из первой урны переложили во вторую 1 шар. Тогда вероятность того, что из второй извлекли белый шар равна…0,47
Законы распределения вероятностей случайных величин
14/1Среднее число вызовов такси, поступающих диспетчеру за одну минуту, равно 4. Тогда вероятность того, что за три минуты поступит ровно 10 вызовов, можно вычислить как…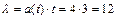 ,
, 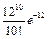
14/2Среднее число заявок, поступающих на предприятие бытового обслуживания за один час, равно 3. Тогда вероятность того, что за 2 часа поступит 5 заявок, можно вычислить как…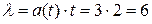 ,
, 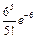
14/3Случайная величина Х задана плотностью вероятности вида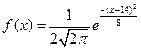 .Тогда вероятность попадания ее значений в интервал (13; 17) можно вычислить как…., где Ф(х)- функция Лапласа
.Тогда вероятность попадания ее значений в интервал (13; 17) можно вычислить как…., где Ф(х)- функция Лапласа
14/4Случайная величина Х задана плотностью вероятности вида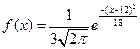 .Тогда вероятность попадания ее значений в интервал (9; 15) можно вычислить как…., где Ф(х)- функция Лапласа
.Тогда вероятность попадания ее значений в интервал (9; 15) можно вычислить как…., где Ф(х)- функция Лапласа
Числовые характеристики случайных величин
15/1 Непрерывная СВ задана функцией распределения вида
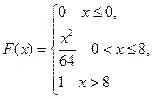 Тогда М(х) и Д(х) равно
Тогда М(х) и Д(х) равно
15/2. Задан закон распределения дискретной случайной величины. Найти М(х), Д(х)
 | -1 | ||
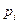 | 0,4 | 0,4 | 0,2 |
15/3. Дискретная случайная величина Х задана законом распределения. Найти М(х), Д(х)
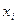 | -1 | ||
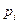 | 0,4 | 0,4 | 0,2 |
15/4Непрерывная случайная величина X задана плотностью распределения вероятностей: 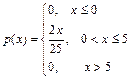 . Тогда Д(х) равна …
. Тогда Д(х) равна …
15/5Мат ожидание случайной величины Х, заданной законом распределения
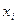 | ||
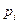 | Р1 | Р2 |
Равно 4,4. найти р2
Основные понятия и задачи МС
16/1. Из генеральной совокупности Х извлечена выборка объема n=50
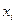 | ||||
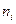 |
Тогда ее эмпирическая функция распределения вероятностей 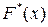 будет равна
будет равна
16/2 Из генеральной совокупности извлечена выборка объема n=120
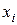 | ||||
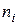 | 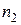 | 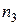 |
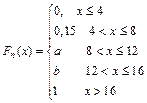 .Тогда значения a и b могут ,быть равны
.Тогда значения a и b могут ,быть равны
а=45, b=80; а=50, b=80; а=55, b=76; а=90, b=76;
16/3 Из генеральной совокупности извлечена выборка объема n=50. Тогда эмпирическая функция распределения равна
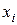 | ||||
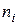 |
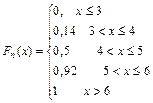 .
.
16/4Из генеральной совокупности извлечена выборка объема n=50. Тогда эмпирическая функция распределения равна
 | ||||
 |
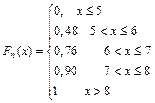 .
.
16/5Из генеральной совокупности X извлечена выборка объема n=100. Тогда ее эмпирическая функция распределения вероятностей 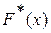 имеет вид …
имеет вид …
