Тема 5. Формула Пуассона. Локальная и интегральная формулы Муавра - Лапласа
1. Формула Пуассона
Использование формулы Бернулли при больших значениях 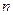 и
и 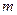 вызывают большие трудности. Например, при 1000 подбрасываниях монеты необходимо определить вероятность того, что «герб» выпадет ровно 150 раз. В этом случае
вызывают большие трудности. Например, при 1000 подбрасываниях монеты необходимо определить вероятность того, что «герб» выпадет ровно 150 раз. В этом случае 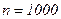 ,
, 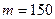 ,
, 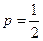 (выпадение «герба»),
(выпадение «герба»), 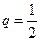 (выпадение «решки»). Формула Бернулли примет вид:
(выпадение «решки»). Формула Бернулли примет вид: 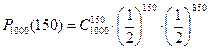 .
.
Вычисления будут очень громоздкими, поэтому возникает необходимость в отыскании приближенных формул для вычисления 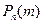 , обеспечивающих необходимую точность. Такие формулы дают нам предельные теоремы; они содержат так называемые асимптотические формулы, которые при больших значениях испытаний дают сколь угодно малую относительную погрешность. Рассмотрим три предельные теоремы, содержащие асимптотические формулы для вычисления вероятности при
, обеспечивающих необходимую точность. Такие формулы дают нам предельные теоремы; они содержат так называемые асимптотические формулы, которые при больших значениях испытаний дают сколь угодно малую относительную погрешность. Рассмотрим три предельные теоремы, содержащие асимптотические формулы для вычисления вероятности при 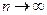 .
.
Теорема Пуассона. Если число испытаний неограниченно увеличивается 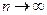 и вероятность
и вероятность 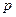 наступления события
наступления события  в каждом испытании неограниченно уменьшается
в каждом испытании неограниченно уменьшается 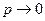 , но так, что их произведение является постоянной величиной
, но так, что их произведение является постоянной величиной 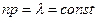 , то вероятность
, то вероятность 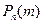 удовлетворяет предельному равенству
удовлетворяет предельному равенству
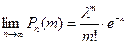
или
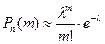 ,
, 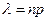 .
.
Формулу Пуассона обычно используют в случае, когда λ 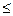 10.
10.
Пример 1. Завод отправляет в некоторый город 1500 автомобилей. Вероятность того, что в пути машина может получить повреждение, равна 0,002. Найти вероятность того, что в пути будет повреждено не более 4-х автомобилей.
Решение. Событие  – в пути будет повреждено не более 4-х автомобилей, т.е. 0, 1, 2, 3, 4.
– в пути будет повреждено не более 4-х автомобилей, т.е. 0, 1, 2, 3, 4.
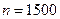 ,
, 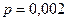 ,
, 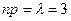 .
.
По формуле Пуассона
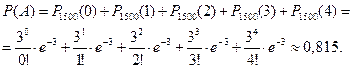
2. Локальная теорема Муавра – Лапласа
Теорема. Если вероятность 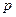 наступления события
наступления события  в каждом испытании постоянна и отлична от 0 и 1, а число независимых испытаний достаточно велико, то вероятность
в каждом испытании постоянна и отлична от 0 и 1, а число независимых испытаний достаточно велико, то вероятность 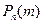 может быть вычислена по приближенным формулам:
может быть вычислена по приближенным формулам:
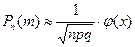 ,
,
где 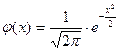 ,
, 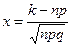 .
.
Функция 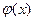 называется функцией Гаусса.
называется функцией Гаусса.
Свойства функции 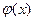 .
.
1. Функция 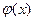 - четная, т.е.
- четная, т.е. 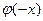 =
= 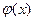 .
.
2. Функция 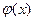 - монотонно убывает, при
- монотонно убывает, при 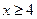 можно считать, что
можно считать, что 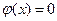 .
.
Пример 2. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение. 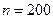 ,
, 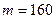 ,
, 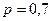 ,
, 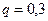 .
.
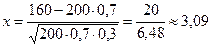 .
.
Учитывая, что 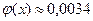 , получим
, получим
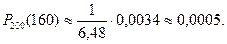
3. Интегральная теорема Муавра – Лапласа
В тех случаях, когда требуется вычислить вероятность того, что в 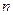 независимых испытаниях событие
независимых испытаниях событие  появится не менее
появится не менее 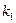 раз и не более
раз и не более 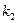 раз, т.е.
раз, т.е. 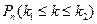 используют интегральную теорему Муавра – Лапласа.
используют интегральную теорему Муавра – Лапласа.
Теорема. Если вероятность наступления 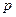 наступления события
наступления события  в каждом испытании постоянна и отлична от 0 и 1, то вероятность
в каждом испытании постоянна и отлична от 0 и 1, то вероятность 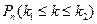 может быть найдена по приближенной формуле
может быть найдена по приближенной формуле
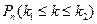
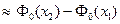 ,
,
где 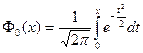 ,специальная функция, называемая нормированной функцией Лапласа,
,специальная функция, называемая нормированной функцией Лапласа,
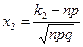 ,
, 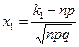 .
.
Свойства функции 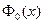 .
.
1. Функция 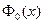 - нечетная, т.е.
- нечетная, т.е. 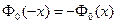 .
.
2. Функция 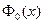 монотонно возрастает, т.е. при
монотонно возрастает, т.е. при 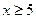 можно считать, что
можно считать, что 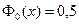 .
.
Имеются таблицы приближенных значений функции 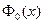 , которыми удобно пользоваться для решения задач.
, которыми удобно пользоваться для решения задач.
Пример 3. Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия бракуется, т.е. возвращается в цех. Какова вероятность того, что партия будет принята?
Решение. 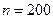 ,
, 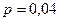 – вероятность бракованного изделия,
– вероятность бракованного изделия, 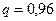 – вероятность хорошего изделия.
– вероятность хорошего изделия.
Вероятность принятия всей партии, т.е. 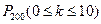 можно найти по формуле:
можно найти по формуле: 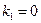 ,
, 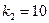 ,
,
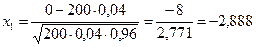 ,
,
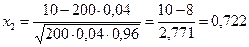 ,
,
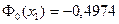 ,
,
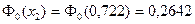 ,
,
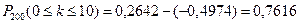 .
.
