Формы законов распределения дискретной случайной величины
Пусть  – дискретная случайная величина, которая принимает значения
– дискретная случайная величина, которая принимает значения 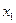 ,
, 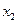 ,...,
,..., 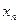 с некоторыми вероятностями
с некоторыми вероятностями 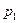 ,
, 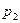 ,...,
,..., 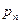 .
.
Наиболее простой формой закона распределения дискретной случайной величины является ряд распределения – таблица, в которой представлены возможные значения случайной величины и вероятности, с которыми случайная величина принимает то или иное значение:
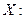 | 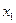 | 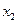 | 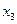 | … | 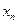 |
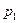 | 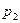 | 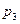 | … | 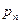 |
Так как в одном испытании случайная величина принимает только одно возможное значение, то события 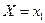 ,
, 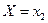 ,...,
,..., 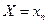 образуют полную группу несовместных событий, т.е. сумма их вероятностей равна 1:
образуют полную группу несовместных событий, т.е. сумма их вероятностей равна 1:
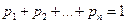 .
.
Другой способ представления дискретной случайной величины – графическое представление ряда распределения – полигон (или многоугольник) распределения вероятностей. Для того, чтобы построить полигон распределения, надо по оси ОХ откладывать значения случайной величины, а по оси ОY – соответствующие вероятности.
Пример полигона распределения представлен на рисунке 1.
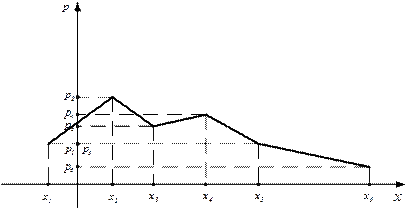
Рис.1.
Закон распределения случайной величины (дискретной или непрерывной) можно задать при помощи функции распределения
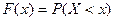 .
.
Значение функции распределения в точке 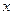 есть вероятность того, что случайная величина
есть вероятность того, что случайная величина  примет значение, меньшее
примет значение, меньшее 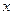 .
.
В случае дискретной случайной величины функция распределения является кусочно-непрерывной функцией
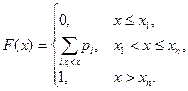
Пример графика функции распределения представлен на рисунке 2.
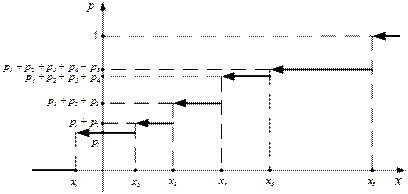
Рис. 2.
Пример 1. Дан ряд распределения случайной величины  :
:
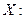 | ||||
| 0,4 | 0,1 | 0,3 | 0,2 |
Найти и изобразить графически ее функцию распределения.
Решение.
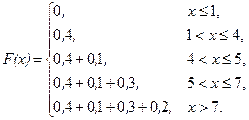
или 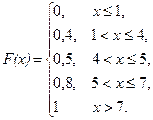
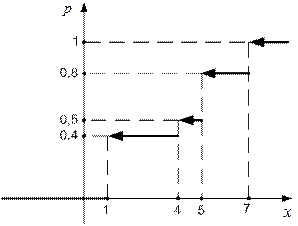
Рис. 3.
Пример 2. Задают ли законы распределения дискретной случайной величины следующие таблицы:
а)
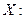 | ||||
| 0,1 | 0,4 | 0,3 | 0,2 |
б)
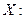 | ||||
| 0,1 | 0,2 | 0,3 | 0,5 |
Решение. Проверяем условие нормировки:
а) 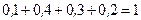 ,
,
б) 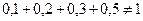 .
.
В случае б) условие нормировки не выполняется, значит, данная таблица не задает закон распределения дискретной случайной величины.
Пример 3. Подбрасываются две монеты. Рассматривается случайная величина  – число выпадений гербов на обеих монетах. Написать закон распределения вероятностей.
– число выпадений гербов на обеих монетах. Написать закон распределения вероятностей.
Решение. в результате опыта возможны следующие исходы: два герба, герб и решка или две решки. Соответственно случайная величина может принимать следующие значения:
0 – в случае, когда выпали две решки,
1 – в случае, когда на одной монете выпал герб, а на другой решка,
2 – в случае, когда выпали два герба.
Вероятность того, что выпали две решки, равна
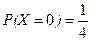 ,
,
герб и решка – 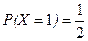 ,
,
два герба – 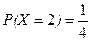 .
.
Таким образом, получаем ряд распределения:
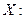 | |||
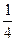 | 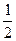 | 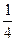 |
Пример 4. Вероятностный прогноз для величины  – процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев – дан в виде закона распределения:
– процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев – дан в виде закона распределения:
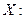 | ||||||
| 0,1 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 |
Найти вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 36% годовых.
Решение. Прирост суммы на банковском депозите при условии 3% в месяц (36% годовых / 12 месяцев) составит через 6 месяцев ((1,03)6-1)∙100%=19,4%. Вероятность того, что покупка акций выгоднее банковского депозита, определяется суммой вероятностей, соответствующих более высокому росту курса акций:
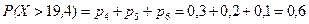
Пример 5. В лотерее разыгрывается: автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью 250 ден.ед., 5 видеомагнитофонов стоимостью 200 ден.ед. Всего продается 1000 билетов по 7 ден.ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет.
Решение. Возможные значения случайной величины  – чистого выигрыша на один билет – равны: 0-7=-7 ден. ед. (если билет не выиграл), 200-7=193, 250-7=243, 5000-7=4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4, и 1, и, используя классическую формулу вероятностей, получим:
– чистого выигрыша на один билет – равны: 0-7=-7 ден. ед. (если билет не выиграл), 200-7=193, 250-7=243, 5000-7=4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4, и 1, и, используя классическую формулу вероятностей, получим:
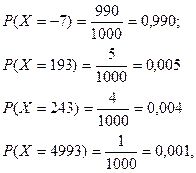
Таким образом, ряд распределения имеет вид:
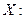 | -7 | |||
| 0,990 | 0,005 | 0,004 | 0,001 |
