Обучение решению задач
Задачи в обучении математике особенных учащихся занимают важное место. Это объясняется их большой коррекционно-воспитательной и образовательной ролью. При решении задач у особенных учащихся развивается произвольное внимание, наблюдательность, логическое мышление, речь, сообразительность. Решение задач способствует развитию таких познавательных процессов, как анализ, синтез, сравнение, обобщение. В процессе решения задач учащиеся учатся планировать и контролировать свою деятельность, овладевают приемами самоконтроля (проверка задачи, прикидка ответа, решение задачи разными способами и др.), у них воспитывается настойчивость, воля, развивается познавательный интерес. Решение задач способствует расширению кругозора учащихся, обогащению их новыми знаниями об окружающей действительности. Велика роль задач в подготовке особенных школьников к жизни, дальнейшей трудовой деятельности. Именно упражнения в составлении и решении задач помогают учащимся видеть в окружающей действительности факты и закономерности, которые используются в математике. При решении задач учащиеся учатся переводить отношения между предметами и величинами на «язык математики».
Умением решать задачи особенные учащиеся овладевают с большим трудом. Трудности в решении задач у рассматриваемой категории детей связаны с недостаточным пониманием предметно-действенной ситуации, отраженной в задаче, и математических связей и отношений между числовыми данными, также между данными и искомыми. В силу стереотипности действий, характерной для большинства особенных детей, они решают задачи шаблонными способами, руководствуясь случайными ассоциациями, вызванными созвучием слов и выражений. Уподобление одних задач другим – наиболее часто встречающийся вид ошибок, тат как осознание сходства и различия задач представляет для детей рассматриваемого контингента определенные трудности. Знание специфики решения задач особенными учащимися помогает учителю избрать наиболее целесообразные пути преодоления трудностей. В процессе обучения решению задач следует избегать натаскивания в решении задач определенного вида, надо учить сознательному подходу к решению задач, учить ориентироваться в жизненной ситуации, описанной в задаче, учить осознанному выделению данных и искомого задачи, установлению взаимосвязи между ними, осознанному выбору действий.
Далее предметом нашего изучения будут сюжетные задачи. В деятельности по решению сюжетной задачи можно выделить следующие этапы: 1) работа над содержанием задачи; 2) поиск решения задачи; 3) решение и запись решения задачи, формулировка ответа; 4) проверка решения задачи; 5) последующая работа над решенной задачей. Рассмотрим подробнее выделенные этапы.
1 этап. Последовательность работы над усвоением содержания задачи: разбор непонятных слов или выражений, которые встретятся в тексте задачи; чтение текста задачи учителем и учащимися; выделение условия и требования задачи; запись условия задачи; выявление связей между данными задачи (какой процесс отражается, какие величины описывают данный процесс, каким основным отношением связаны величины); повторение задачи по вопросам; воспроизведение одним из учащихся полного текста задачи.
Работа над отдельными словами и выражениями должна вестись до предъявления задачи, а не тогда, когда учитель знакомит учащихся с содержанием задачи, иначе словарная работа разрушает структуру задачи, уводит учащихся от понимания математического содержания задачи, зависимостей между данными.
Чтение текста задачи осуществляется выразительно, выделяя голосом математические выражения, главный вопрос задачи, делая логические ударения на тех предложениях или сочетаниях слов, которые прямо указывают на определенное действие. Между условием задачи и вопросом следует сделать паузу, если вопрос стоит в конце задачи. Нужно помнить, что школьники рассматриваемой категории, если их этому специально не учить, не всегда могут самостоятельно правильно прочитать задачу, расставить логические ударения, затрудняются с выделением вопроса задачи, если он стоит в ее начале или середине.
Восприятие текста задачи только на слух затруднительно для особенных школьников. При восприятии текста задачи необходимо использовать не только слуховые, но и зрительные, а если возможно, то и кинестетические анализаторы.
Задачу следует иллюстрировать. Выполняя рисунок или иллюстрируя задачу предметами, учащиеся глубже проникают в предметно-действенную ситуацию задачи и легче устанавливают зависимость между данными, а также между данными и искомыми. Постепенно учащиеся переходят от «опредмечивания» содержания задачи к «воображению» ими предметной ситуации.
Наряду с конкретизацией содержания задачи с помощью предметов, рисунков и т.п. в практике работы учителей классов КРО широкое распространение получили следующие формы записи содержания задачи: сокращенная; сокращенно-структурная; схематическая; графическая; табличная. Указанным формам записи содержания задач особенных школьников необходимо учить так, чтобы они самостоятельно могли выбрать наиболее рациональную форму и записать условие задачи. При этом учителю необходимо соблюдать систему, поэтапность в обучении [20]:
1. После ознакомления учащихся с текстом задачи учитель сам
дает краткую запись содержания задачи на доске, учащиеся записывают ее одновременно с учителем в тетрадь.
2. После разбора условия задачи краткую запись на доске
делает ученик под руководством учителя, при активном участии
учащихся всего класса. С этой целью учитель просит ученика
прочитать фрагмент задачи и спрашивает, как можно записать эту
часть задачи кратко, зарисовать или начертить.
3. Вызванный к доске ученик самостоятельно читает задачу и
дает ее краткую запись под контролем учителя. Учащиеся также
выполняют это задание самостоятельно и сверяют свою запись с
записью на доске.
4. Самостоятельная запись условия задачи учащимися.
Краткая форма записи задачи должна быть составлена так, чтобы ученик мог по ней воспроизвести условие задачи или составить задачу.
Лучшему восприятию и пониманию задачи способствует ее повторение по вопросам.
2 этап. На этапе поиска решения задачи учащиеся, отвечая на вопросы учителя, поставленные в определенной логической последовательности, подводятся к составлению плана решения задачи и выбору действий. Для того чтобы ученики правильно поняли жизненно-практическую ситуацию задачи и смогли перевести зависимость между предметами и величинами на «язык математики», учитель проводит беседу с учащимися, которая называется разбором задачи. В беседе устанавливается зависимость между данными и искомым. При разборе содержания задачи нового вида учитель ставит вопросы так, чтобы подвести учащихся к правильному и осознанному выбору действий. Разбор задачи можно начинать с числовых данных (сверху) и вести учащихся к главному вопросу задачи. Разбор задачи можно начинать и от главного вопроса задачи (снизу) – это более целенаправленный (на составление плана решения) и предпочтительный ход рассуждений. При разборе уже знакомых учащимся задач не следует прибегать к многословным рассуждениям. Иногда достаточно поставить перед учащимися один-два узловых вопроса, чтобы путь решения задачи был ученикам ясен. Далее устно составляется план и намечается последовательность действий.
3 этап. Решение задачи, запись решения и формулировка ответа. На рассматриваемом этапе происходит реализация плана решения, то есть запись решения задачи с использованием принятых обозначений, символов, терминов и обоснованием отдельных шагов решения. Формулируется ответ (в краткой или полной форме).
4 этап. Проверка решения задачи. Так как функция контроля у особенных школьников ослаблена, то проверка решения задач имеет не только образовательное, но и коррекционное значение.
В младших классах КО и КРО необходимо: проверять словесно сформулированные задачи, производя действия над предметами, если, конечно, это возможно; проверять реальность ответа (соответствие его жизненной действительности); проверять соответствие ответа условию и вопросу задачи.
Проверка решения задачи другим способом ее решения возможна с 4-го класса. Для осуществления проверки задачи очень полезна прикидка ответа до решения задачи.
Для контроля правильности решения задачи можно использовать некоторые элементы программированного контроля. Например, учитель пишет на доске ответы конечного и промежуточных действий, только не в том порядке, который необходим при решении задачи; учащиеся (при самостоятельном решении) сверяют ответы промежуточных действий и «запрограммированные» ответы. Этот прием очень полезен тем, что ученик сразу получает подкрепление правильности или, наоборот, ошибочности своих действий. При ошибочности решения он ищет новые пути решения.
5 этап. Последующая работа над решенной задачей. Учитель классов КО и КРО зачастую не может быть уверен, что решение задачи (хотя задача разобрана и решена) понято всеми учениками. Поэтому очень полезно провести работу по закреплению решения этой задачи.
Работа по закреплению решения задачи может быть проведена различными приемами [20].
1. Ставятся узловые вопросы по содержанию задачи.
2. Предлагается рассказать весь ход решения задачи с обоснованием выбора действий.
3. Ставятся вопросы к отдельным действиям или вопросам.
Для особенных учащихся школы важно не количество решенных аналогичных задач, а понимание предметной ситуации и зависимости между данными. Этой цели служит последующая работа над решенной задачей, которую можно рассматривать как важный прием, формирующий умение решать задачи данного вида. Рассмотрим несколько вариантов последующей работы над решенной задачей: изменение отношений между данными условия задачи и выяснение, как это изменение отразится на решении задачи; изменение вопроса задачи; изменение условия задачи, привнесение в него дополнительного данного или изъятие какого-либо данного; изменение числовых данных, сюжета задачи, решение задачи, аналогичной данной.
Конечно, не над каждой решенной задачей следует проводить такую последующую работу. Однако надо помнить, что это один из полезных приемов, который учит самостоятельному решению задач, пониманию зависимости между данными, между данными и искомым, а также тому, как эта зависимость отражается на выборе арифметических действий.
Для того чтобы учащиеся научились решать задачи данного вида и приобрели навык обобщенного способа решения таких задач, требуется многократное решение достаточного количества задач. Однако решать подряд задачи одного вида не следует, так как это может привести к «натаскиванию» учащихся в их решении только на короткий срок. Полезно чередовать решение разных видов задач, сравнивать их, выделять черты сходства и различия. Этому способствует использование приема сравнения. При сравнении учащиеся лучше понимают жизненную предметную ситуацию задачи, те существенные, а не случайные, чисто внешние признаки, которые влияют на выбор действий при решении задачи.
Лучшему пониманию предметного содержания задач, зависимости между данными и искомыми способствует решение задач с лишними или недостающими числовыми данными или данными, записанными не числами, а словами.
На рассматриваемом этапе учителя классов КРО широко используют составление задач самими учащимися. Легче всего для особенных учащихся частичное составление задач (в готовое условие вставляются пропущенные числовые данные; к готовому условию ставятся вопросы; к вопросу подбирается условие задачи и т.п.).
Для полного составления задач учащимся можно предложить самые разнообразные варианты: составление задачи по инсценировке; составление задачи по иллюстрациям: картине, плакату, схеме, чертежу, краткой записи условия; составление задач по числовым данным; составление задач по готовому решению; составление задачи по готовому плану; составление задач на указанное арифметическое действие; составление задачи определенного вида; составление аналогичных задач.
Следует стимулировать составление учащимися задач с разнообразными фабулами. Это способствует развитию их воображения, смекалки, инициативы. Очень полезно, когда для составления задач учащиеся привлекают материал, «добываемый» ими во время экскурсий, из справочников, газет, журналов, хронологических таблиц. Очень полезно, когда числовые данные получают сами учащиеся путем измерений, выполнения различных заданий практического характера. Это способствует осуществлению связи преподавания математики с трудом, будет лучше готовить учащихся к жизни.
Все вышеперечисленные приемы могут быть широко использованы при решении задач, как в младших, так и старших классах КРО.
Проиллюстрируем сформулированные выше теоретические положения на конкретном примере организации деятельности учителя и учащихся при решении сюжетной задачи.
Задача. На трех участках общей площадью 180 га посажена капуста. Первый участок на 60 га меньше второго, который на 30 га больше третьего. С первого участка собрали по 13 ц с 1 га, со второго – по 12 ц, а с третьего – по 11 ц с 1 га. Сколько центнеров капусты собрали?
1 этап. Читаем задачу, затем предлагаем учащимся составить по условию задачи таблицу или чертеж, или самим найти наиболее удачную форму записи условия задачи. Возможна следующая последовательность вопросов и ответов на них.
Учитель: «Можете ли вы определить, к какому типу задач относится данная задача? Ответ обоснуйте».
Учащийся 1: «Эта задача относится к задачам на «части и целое».
Учитель: «Для того чтобы определить, что в задаче выполняет роль частей и целого, что мы еще должны выяснить?»
Учащийся 1: «Какие величины описывают ситуацию в задаче».
Учащийся 2: «Площадь участков, сколько собрали центнеров с 1 га на каждом участке и количество собранной капусты с каждого участка».
Учитель: «Как называется величина, обозначающая сколько собрали центнеров с 1 гектара?»
Учащийся 3: «Урожайность».
Учитель: «Теперь можно начинать составлять таблицу. Подумайте, сколько столбцов и строк будет в таблице. Почему?»
Учащийся 1: «В задаче три величины и три участка, значит, получаем таблицу 3х3 плюс 1 столбик и 1 строчка на названия данных».
Учащийся 3: «А я считаю, что нужна таблица 5х4, так как, кроме строк для обозначения «частей», потребуется строка для «целого».
Далее учитель организует работу по заполнению таблицы.
| Участок | Площадь, га | Урожайность, ц | Количество, ц |
| I | Ч на 60 м. 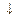 | Ч | |
| II | Ч | Ч | |
| III | Ч на 30 б. 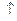 | Ч | |
| Всего | Ц 180 | ? Ц |
2 этап. Поиск решения задачи может быть проведен аналитико-синтетическим путем. Анализ может быть представлен, например, в виде таблицы. Форма работы на этом этапе предпочтительна фронтальная в виде беседы. Из анализа получаем план решения задачи: 1. Находим площади участков. 2. Определяем, сколько собрано с каждого участка. 3. Вычисляем, сколько собрано всего.
| Чтобы узнать | Надо определить |
| Сколько центнеров капусты собрали | Сколько центнеров капусты собрали с каждого участка |
| Сколько центнеров капусты собрали с участка | Какова площадь этого участка и сколько собирали с 1 га на этом участке (известно) |
| Какова площадь I участка | ? (меньше II на 60 га) |
| Какова площадь II участка | ? |
| Какова площадь III участка | ? (больше II на 30 га) |
3 этап. Анализ задачи приводит к выводу: чтобы найти площади участков, надо площадь какого-нибудь одного из них выбрать за неизвестное, с помощью которого можно выразить площади остальных участков, и, используя установленную зависимость между данными задачи – «части и целое», составить уравнение. Возникает вопрос: что следует принять за неизвестное? Выбор неизвестного можно оформить в виде следующей таблицы.
| Участок | Площадь, га | Площадь, га | Площадь, га |
| I | Ч x | Ч х–60 | Ч (х+30)–60 |
| II | Ч х+60 | Ч х | Ч х+30 |
| III | Ч (х+60)–30 | Ч х–30 | Ч х |
| Всего | Ц 180 | Ц 180 | Ц 180 |
Обращая внимание на заполнение ячеек таблицы, учащиеся приходят к выводу, что за неизвестное следует принять площадь II участка. Таким образом, получили, что метод решения в данном случае – комбинированный: первая часть (нахождение площадей) – алгебраический, вторая часть (нахождение искомой величины) – арифметический. Составляем уравнение ((х–60) + х + (х–30) = 180), решаем его, находим, что площадь I участка – 30 га, площадь II участка – 90 га, площадь III участка – 60 га. Далее, находим, что с I участка собрали 390 ц, со II участка – 1080 ц, с III участка – 660 ц. Всего со всех трех участков собрали 2130 ц капусты.
4 этап. Можно проверить решение данной задачи, выяснив, имеются ли между найденными величинами те же самые отношения, которые описаны в условии задачи.
5 этап. Проводится работа по закреплению решения задачи, а также дальнейшая работа над решенной задачей путем использования, например, следующих приемов: изменение отношений между данными условия задачи и выяснение, как это изменение отразится на решении задачи; изменение вопроса задачи; изменение условия задачи, привнесение в него дополнительного данного или изъятие какого-либо данного; изменение числовых данных, сюжета задачи, решение задачи, аналогичной данной.
Изучение теорем.
Теорема – утверждение, истинность которого устанавливается посредством доказательства. С теоремами учащиеся имеют дело в различных разделах школьного курса математики, но наиболее полно они представлены в курсе геометрии.
Принципы подхода к обучению особенных учащихся теоремам и их доказательствам следуют из трех соображений.
Во-первых, теорема – это новый материал, подлежащий изучению, и с этой точки зрения в изучении теоремы можно выделить следующие этапы: подготовка к изучению нового (пропедевтика); мотивация изучения нового материала; введение нового – организация его восприятия, понимания; закрепление; применение.
Во-вторых, теорема является задачей на доказательство, выражающей некоторое важное отношение, свойство, и поэтому на методику изучения теорем распространяются рекомендации, относящиеся к различным этапам решения задач.
В третьих, изучая с особенными детьми теоремы, следует учитывать специфику их познавательной и эмоционально-волевой деятельности. Содержание курса математики должно быть скорректировано таким образом, чтобы изучение теорем осуществлялось на доступном для рассматриваемой категории школьников уровне.
Охарактеризуем кратко представленные соображения.
Пропедевтика заключается в актуализации необходимых для изучения теоремы знаний. Пропедевтика также предусматривает снятие определенных трудностей – вынесение некоторых моментов доказательства в самостоятельные задачи, которые можно решить до доказательства теоремы. Это особенно актуально для рассматриваемого контингента детей, которых трудности при проведении доказательства иногда вынуждают забыть о самом доказательстве. В качестве примера рассмотрим теорему о соотношении между сторонами и углами треугольника. Доказательство этой теоремы опирается на следующий прием: чтобы сравнить два угла, надо ввести в рассмотрение третий угол, связанный с этими двумя углами. При доказательстве теоремы используются свойства равнобедренного треугольника и свойство внешнего угла треугольника. Все эти знания необходимо «освежить» в памяти учащихся перед доказательством. Это можно осуществить либо путем опроса учащихся, либо путем выполнения упражнений. Второй путь эффективнее первого, так как при выполнении упражнений аккумулируется восприятие идеи доказательства теоремы и знания, необходимые для доказательства. Примером такого упражнения является следующее: «На стороне ВС треугольника АВС взята точка D так, что AB=BD. Доказать, что  ВАD больше
ВАD больше  ВСА». Необходимо специально акцентировать внимание школьников на методе доказательства: сравнение двух углов (
ВСА». Необходимо специально акцентировать внимание школьников на методе доказательства: сравнение двух углов (  ВАD и
ВАD и 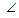 ВСА) осуществляется путем введения третьего угла (
ВСА) осуществляется путем введения третьего угла (  ВDA), связанного с данными двумя углами.
ВDA), связанного с данными двумя углами.
Мотивация предполагает повышение интереса к изучаемой теореме. Для этого полезно перед изучением теоремы создать на уроке проблемную ситуацию, разбор которой мотивировал бы необходимость изучения этой теоремы. С этой целью можно использовать различные практические ситуации и мотивационные упражнения.
Организация восприятия и понимания теоремы начинается с ознакомления учащихся с формулировкой теоремы, что может быть осуществлено разными способами: а) учитель подготавливает учащихся к самостоятельному «открытию теоремы»; б) учитель организует работу по сознательному восприятию и пониманию учащимися новой теоремы, формулировка которой сообщается им в готовом виде; в) учитель формулирует теорему сам, без предварительной подготовки учащихся, а затем направляет их усилия на ее усвоение; г) формулировка отрабатывается учащимися самостоятельно по учебнику.
Далее необходима целенаправленная работа по изучению содержания и структуры теоремы. Здесь целесообразно использование следующих методических приемов: выделение условия и заключения теоремы, ее формулировка в условной форме; иллюстрация к содержанию теоремы (чертеж, рисунок, схема, модель); краткая запись содержания теоремы с опорой на чертеж и с использованием необходимой символики; определение вида теоремы, анализ ее логической структуры; упражнения на самостоятельное формулирование теоремы, ее переформулирование в более удобной форме; рассмотрение частных и особых случаев, если они имеются.
Важнейшим этапом в изучении теоремы является ее доказательство.
На этом этапе обдумывается и коллективно обсуждается идея доказательства, осуществляется и оформляется доказательство теоремы.
Ознакомить учащихся с доказательством теоремы можно различными приемами.
Прием 1. Для изложения доказательства теоремы учитель использует частично-поисковый метод, таким образом, активизация класса происходит посредством эвристической беседы, которую ведет учитель с учащимися. Этот метод создает дидактические трудности, преодоление которых направляет и стимулирует интеллектуальную деятельность школьников.
Прием 2. Учитель излагает доказательство теоремы объяснительно-иллюстративным методом в форме краткого рассказа, не прерывая его вопросами в адрес учащихся. Этот прием обеспечивает высокое качество изложения доказательства, позволяет учащимся легче воспринимать последовательность, обоснованность и другие стороны доказательства. Речь учителя в таком случае выступает для школьников научным и логическим образцом оформления доказательства; они учатся строить умозаключения, делать обобщения и выводы. Объяснительно-иллюстративный метод изложения доказательства теоремы, в отличие от частично-поискового, позволяет экономить время урока. Этот метод обычно используют в тех случаях, когда доказательство небольшое по объему или же когда теорема доказывается принципиально новым для учащихся способом.
К какому бы виду ни относилось то или иное объяснение, к нему следует предъявлять такие требования: обеспечение целесообразного соединения активности учителя и активности учащихся; соответствие методов, приемов и средств обучения, используемых учителем при объяснении, выбранному виду объяснения; соблюдение полной структуры объяснения (подготовительный этап, собственно объяснение, заключительный этап); комплексная реализация воспитывающих, развивающих и обучающих функций объяснения; выбор оптимального варианта объяснения на основе тщательного анализа специфических условий протекания объяснения (особенности учебного материала, программные требования, задачи конкретного урока, психолого-педагогические особенности школьников, личные и профессиональные качества учителя), ориентируясь на вид объяснения.
Прием 3. Метод самостоятельного изучения доказательства по учебнику. Учитель выступает здесь в роли консультанта и организатора. Учащимся даются указания к выполнению работы, обращается внимание на основные и наиболее трудные моменты в доказательстве. Для облегчения самостоятельного изучения доказательства теоремы учитель может предложить учащимся готовый план. Заметим, что в учебниках доказательство теорем иногда проводится в форме неполных силлогизмов и тогда задача ученика состоит в том, чтобы восполнить недостающие звенья в рассуждениях.
При изучении теорем в классах КРО чаще всего используется второй прием ознакомления учащихся с доказательством, эпизодически – первый прием, третий же прием, учитывая недостатки и особенности детей указанной категории, используется крайне редко.
После получения и осуществления идеи доказательства, записи доказательства теоремы необходимо закрепление полученного доказательства. Оно предшествует закреплению и применению формулировки теоремы. При осуществлении закрепления полученного доказательства можно с помощью вопросов, обращенных к учащимся, снова «пройтись» по всему доказательству, попросить объяснить отдельные шаги доказательства, перечислить все аксиомы, теоремы и определения, которые используются в доказательстве, выяснить, где используется какое-либо данное, все ли условия оказались использованными, какое и почему дополнительное построение оказалось полезным при поиске доказательства, в чем заключается основная идея доказательства, что оказалось несущественным для доказательства и что может быть изменено, нет ли других способов доказательства рассматриваемой теоремы, всегда ли полученное доказательство имеет смысл.
Учеными доказана эффективность приема неоднократного повторения доказательства теоремы (схематическое и развернутое, «в три приема»), направленного на достижение глубокого понимания учащимися объяснения. Повторные доказательства должны проводиться на различных уровнях сложности. Вначале объяснение проводится с опорой на рисунок и раскрывается основная идея доказательства (опускаются обоснования, смысл которых понятен учащимся из наглядных соображений). Затем опущенные обоснования восстанавливаются. При третьем «проходе» доказательство повторяется полностью и оформляется письменно.
Установлено (Г.И. Саранцев; М.Н. Перова и др.), что для слабоуспевающих школьников большую трудность представляет усвоение логики доказательства: выделение отдельных шагов доказательства, их обоснование, установление взаимосвязи между отдельными шагами. Одной из форм работы с особенными учащимися, направленной на усвоение логики доказательства, является использование специальных карточек. На карточке изображается таблица, состоящая из двух колонок. Одна колонка содержит утверждения, другая – их обоснования, причем в колонках имеются пропуски, которые предстоит заполнить ученику. Запишем в виде таблицы (без пропусков) доказательство теоремы о сумме углов треугольника по учебнику А.В. Погорелова.
| I. Утверждения | II. Обоснования |
1. BD║AC. 2. А и D поразные стороны от прямой ВС. 3.  DBC и DBC и  ACB – внутренние накрест лежащие углы при прямых АС и BD и секущей ВС. 4. ACB – внутренние накрест лежащие углы при прямых АС и BD и секущей ВС. 4.  DBC DBC 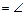 ACB. 5. ACB. 5.  ABD ABD 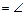 ABC ABC 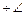 CBD. 6. CBD. 6.  ABD ABD 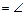 ABC ABC 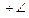 ACB. 7. ACB. 7.  BAC и BAC и  ABD – внутренние односторонние углы при параллельных прямых АС и BD и секущей ВС. 8. ABD – внутренние односторонние углы при параллельных прямых АС и BD и секущей ВС. 8.  BAC BAC 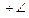 ABD=180°. 9. ABD=180°. 9.  BAC BAC 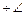 ABC ABC 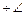 ACB=180°. ACB=180°. | По построению. По построению. По определению внутренних накрест лежащих углов. По свойству внутренних накрест лежащих углов при парал-лельных прямых и секущей. ВС – внутренний луч угла ABD. Утверждения 4, 5. По определению внутренних односторонних углов при параллельных прямых и секущей. По свойству внутренних односторонних углов при параллельных прямых и секущей. Утверждения 6, 8. |
Один из вариантов карточки можно составить на основе данной таблицы, если сделать в ней некоторые пропуски. Например, можно оставить пустыми клетки: II, 1; II, 3–6; I, 7–8; II, 8; I, 2. (Римская цифра означает номер столбца в таблице, а следующие за ней арабские цифры – номер строки в данном столбце.)
Известно, что доказательство теоремы с опорой на один и тот же рисунок ведет к формальному его усвоению. Поэтому необходимо осуществлять доказательство теоремы с опорой на различные рисунки. Однако это вызывает большие трудности у особенных учащихся. Использование указанных карточек способствует преодолению этих трудностей. Карточки могут использоваться при самостоятельной работе учащихся на уроке и при выполнении домашнего задания. Их можно видоизменять с учетом индивидуальных возможностей учащихся. Количество пропусков в карточке зависит от того, как ученик ориентируется в материале. Если хорошо, то пропусков в его карточке больше; если хуже – меньше. (Некоторые учащиеся доказывают теорему без карточек.)
Работа с такими карточками требует от учащихся воспроизведения всей цепи рассуждений, способствует усвоению сущности дедуктивного метода, ускоряет математическое развитие учащихся; корригирует их недостатки.
Еще один прием, позволяющий слабоуспевающим учащимся закрепить доказательство изученной теоремы, – использование тетради с печатной основой. Приведем в качестве примера образец записи в такой тетради доказательства теоремы: «Если в треугольнике ABC медиана BD является высотой, то треугольник ABC – равнобедренный».
Пусть в Δ ABC BD – медиана и__________. Так как BD – медиана, то ________ = ________. Так как BD – высота, то ________ = _________.
Значит, в Δ ABD и Δ BCD AD =_________; BD – __________ сторона;  BDA=______. Значит, по _______ признаку ________ Δ ABD=_____. Отсюда AB=_______, а это означает, что Δ ABC – ___________.
BDA=______. Значит, по _______ признаку ________ Δ ABD=_____. Отсюда AB=_______, а это означает, что Δ ABC – ___________.
В целях облегчения запоминания особенными учащимися формулировок теорем целесообразно их поэлементное усвоение. Для этого формулировка теоремы разбивается на отдельные элементы (в тексте элементы отделяются вертикальной чертой), после чего каждый из элементов используется при выполнении упражнений. Например. «Квадрат двучлена │ равен сумме трех выражений: │ квадрата первого члена, │ удвоенного произведения первого члена на второй│ и квадрата второго члена». Один из учащихся вызывается к доске, другой работает с текстом, остальные выполняют упражнения с последовательным использованием каждого элемента в тетрадях.
Верны ли равенства:
а) 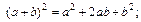 б)
б) 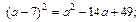
в) 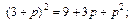 г)
г) 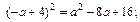
д) 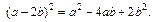
Ученик читает: «Квадрат двучлена», другие учащиеся убеждаются, что выражение, например, 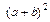 есть квадрат двучлена и т.д., последовательно соотнося каждый элемент формулировки теоремы с соответствующим элементом выражения. Указанное соотнесение может выполняться учащимися самостоятельно при контроле учителем их действий.
есть квадрат двучлена и т.д., последовательно соотнося каждый элемент формулировки теоремы с соответствующим элементом выражения. Указанное соотнесение может выполняться учащимися самостоятельно при контроле учителем их действий.
Существуют и другие, не менее эффективные приемы закрепления теорем, и учитель может выбрать тот из них, который в данный момент будет наиболее эффективен, однако основным средством закрепления теорем является их применение к решению задач.
На этапе практического применения теоремы возможно использование следующих методических приемов: построение «родословной» теоремы; показ места и роли изученной теоремы в данной теме или теории; рассмотрение практических приложений теоремы; обобщение теоремы (если оно возможно); решение задач на применение новой теоремы (задачи, которые используются для отработки теоремы, должны быть разнообразны как по содержанию, так и по методам решения. На первых порах отработки теоремы учащимся следует предлагать алгоритмические задачи, решение которых предполагает непосредственное применение изученной теоремы. Затем учащимся могут быть предложены задачи полуалгоритмического и эвристического характера); упражнения на систематизацию теорем.
Наличие всех рассмотренных этапов при обучении каждой теореме требует большого расхода времени. В полном, развернутом виде все этапы могут быть представлены лишь в отдельных случаях. В различных конкретных ситуациях на первый план выдвигается то один, то другой этап. Предпочтение отдается то поиску формулировки, то обучению записи полученного доказательства, то исследованию – в зависимости от ситуации.
Задания
1. Охарактеризуйте особенности процесса формирования понятий у учащихся классов КРО. Разработайте фрагмент урока по введению определения некоторого понятия.
2. Подберите упражнения для работы с учащимися классов коррекционно-развивающего обучения на каждом из этапов формирования какого-либо алгоритма или правила.
3. Выберите одну из теорем школьного курса геометрии, рекомендованную для изучения учащимся классов с недостаточной математической подготовкой. Покажите все этапы работы над теоремой.
4. Продумайте организацию деятельности особенных учащихся на всех этапах решения выбранной задачи.
Раздел 3. ЧАСТНЫЕ ВОПРОСЫ МЕТОДИКИ КОРРЕКЦИОННО-РАЗВИВАЮЩЕГО ОБУЧЕНИЯ МАТЕМАТИКЕ учащихся с недостаточной математической подготовкой
