Методика изучения некоторого наиболее сложного для усвоения математического материала
В учебном пособии уже рассматривались вопросы, связанные с изучением обыкновенных дробей (п. 6.2); десятичных дробей (п. 6.1); положительных и отрицательных чисел (п. 5.1). Еще одна, достаточно трудная для усвоения учащимися классов КРО, тема, которую мы рассмотрим в рамках данного параграфа, посвящена процентам.
С процентами учащиеся классов КРО знакомятся после изучения целых чисел, обыкновенных и десятичных дробей. Вопросы, связанные с процентами, позволяют сделать курс практико-ориентированным, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, фабулы которых приближены к современной тематике и жизненному опыту детей.
Процент – это дробь со знаменателем 100, имеющая особое название (подобно 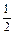 – половина) и особую форму записи (
– половина) и особую форму записи ( 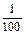 – процент). Слово «процент» обозначается знаком %.
– процент). Слово «процент» обозначается знаком %.
Десятичные дроби со знаменателем 100 наиболее удобны для вычислений, так как во многих мерах метрической системы встречается единичное отношение 100 (1 м = 100 см, 1 руб. = 100 коп., 1 га = 100 а, 1 ц = 100 кг; следовательно, 1 см = 0,01 м, 1 коп. = 0,01 руб., 1 а = 0,01 га, 1 кг = 0,01 ц). 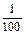 часть числа обозначается так: 1%. Можно записать, что 1 см = 0,01 м = 1% метра, 1 коп. = 0,01 руб. = 1% рубля, 1а = 0,01 га = 1% гектара, 1 кг = 1% центнера. В данном случае мы выразили полученные числа в процентах. Отвлеченные числа также можно выразить в процентах. Учащимся это можно объяснить так: «1% – это
часть числа обозначается так: 1%. Можно записать, что 1 см = 0,01 м = 1% метра, 1 коп. = 0,01 руб. = 1% рубля, 1а = 0,01 га = 1% гектара, 1 кг = 1% центнера. В данном случае мы выразили полученные числа в процентах. Отвлеченные числа также можно выразить в процентах. Учащимся это можно объяснить так: «1% – это 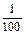 часть числа. Чему же равно все число? Оно в 100 раз больше, т.е.
часть числа. Чему же равно все число? Оно в 100 раз больше, т.е. 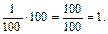 Значит, если
Значит, если 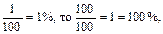 2 = 200%, 5 = 500%, 15 = 1500% и т.д.
2 = 200%, 5 = 500%, 15 = 1500% и т.д.
На основе понятия о проценте и умений выразить (записать) числа в процентах необходимо объяснить значение часто встречающихся на производстве и в быту выражений, например: «Рабочий выполнил норму по обработке деталей на 100%». Это означает, что рабочий обработал за смену то количество деталей, которое было запланировано, например 150 деталей. Если рабочий сделал меньше 150 деталей, то он не выполнил норму, т. е. выполнил ее меньше чем на 100%. Если рабочий сделал больше 150 деталей, то он перевыполнил норму, т. е. выполнил ее больше чем на 100%.
Учащиеся знакомятся не только с выражением целого числа, но и десятичных дробей процентами. В этом случае учитель при объяснении также исходит из определения процента: 0,01 = 1%, следовательно, 0,02 = 2%; 0,05 = 5%; 0,25 = 25%; 0,5 = 50%, так как 0,5 = 0,50 = 50%; 1,7 = 170%. На основании подобных рассуждений, наблюдений и сравнения десятичной дроби и числа, выражающего эту дробь в процентах, некоторые учащиеся могут сделать вывод: «Чтобы десятичную дробь заменить процентами, надо перенести запятую вправо на два знака и поставить знак %». Вместо недостающих знаков ставятся нули. Обыкновенную дробь также можно выразить (заменить) процентами. Ее нужно для этого обратить в десятичную дробь и применить правило замены десятичной дроби процентами, например: 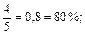
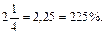
Учащихся классов КРО знакомят и с обратной задачей: выражением процентов в десятичных или обыкновенных дробях. Рассуждения ведутся также исходя из понятия о проценте: 1% = 0,01; 2% = 0,02; 40% = 0,40 = 0,4; 100% = 1; 200% = 2; 150% = 1,5; 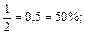
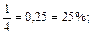
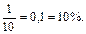
На основе наблюдений и сравнения числа процентов и дроби, выражающей это число, учащиеся подводятся к выводу: «Чтобы выразить проценты десятичной дробью или целым числом, надо запятую перенести на два знака влево и знак % не писать». Например, 20% = 0,2; 300% = 3.
Осознанному усвоению понятия процента способствуют, например, такие упражнения.
1. Выберите для каждого процента в левом столбце соответствующую ему дробь:
| 10% | 0,5 |
| 50% | 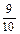 |
| 30% | 0,1 |
| 75% | 0,3 |
| 90% | 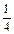 |
| 25% | 0,75 |
2. Для каждой фразы из левого столбца подберите соответствующую фразу в правом:
| 100% учащихся школы | а) половина всех учащихся школы; |
| 25% учащихся школы | б) все учащиеся школы; |
| 10% учащихся школы | в) четверть всех учащихся школы; |
| 50% учащихся школы | г) десятая часть всех учащихся школы; |
3. Туристы проехали 50% пути на поезде и 40% пути на автобусе. Весь ли путь они проехали?
4. В классе 40% девочек. Кого в классе больше – мальчиков или девочек?
5. Что больше:
а) 60% всего класса или половина класса?
б) 10% зарплаты или четверть зарплаты?
в) половина или 45% всего населения страны?
Введение понятия «процент» для особенных учащихся необходимо сочетать с их предметно-практической деятельностью, с опорой на геометрическую наглядность и геометрическое моделирование. С самого начала освоения понятия следует привлекать учащихся к выполнению заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Например:
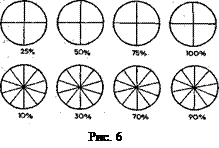 |
Заштрихуйте на рисунке 6 указанную часть круга:
Для учащихся 6 класса КРО предусмотрено решение задач на нахождение одного и нескольких процентов от числа, а также нахождение числа по одному проценту. Задачи на проценты не представляют собой ничего нового для учащихся по сравнению с ранее решавшимися задачами на нахождение одного и нескольких частей от числа и на нахождение числа по одной и нескольким частям. Поэтому, прежде чем решать задачи на проценты, надо повторить решение ранее решавшихся задач и довести до сознания каждого учащегося, что 1% – это тоже дробь 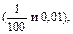 но записанная особым образом.
но записанная особым образом.
Сначала дается понятие вычисления 1% и нескольких процентов от числа и вырабатывается навык выполнения этих действий.
Например, надо найти 1% от 200. Рассуждаем так: 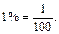 Значит, надо найти
Значит, надо найти 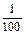 (т.е. взять 1 сотую) от 200, т.е.
(т.е. взять 1 сотую) от 200, т.е. 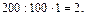
Учащиеся должны решить несколько таких примеров и на основе наблюдений сделать вывод: «Чтобы найти 1% от числа, надо это число разделить на 100». Только после этого учащиеся начнут решать задачи на нахождение 1% от числа типа: «Рабочий получает 1000 руб. 1% от своего заработка он платит налог. Сколько денег рабочий платит?»
Решение.
1) Найдем 1% от 1000 руб.
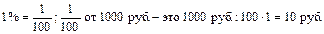
Ответ. Рабочий платит налог 10 руб.
Аналогично подходят и к решению задач на нахождение нескольких процентов от числа. Например, надо найти 5% от 200, т.е. 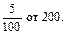 Находим сначала 1%, т. е.
Находим сначала 1%, т. е. 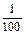 долю от 200
долю от 200 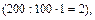 и берем 5 таких долей, т.е. 5%. Значит,
и берем 5 таких долей, т.е. 5%. Значит, 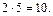 Вычисления записываются так:
Вычисления записываются так: 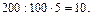
Учитель обязательно должен каждый раз спрашивать: «Что мы получаем, когда делим число на 100? Почему умножаем на число процентов?» Это позволяет особенным учащимся более сознательно относиться к вычислениям.
Задачи на нахождение нескольких процентов от числа целесообразно решать сначала в два действия и только тогда, когда учащиеся осознанно будут относиться к записи решения задачи, содержащим два действия, можно будет записать действия в одну строку.
Например: «В школу привезли 700 учебников. 9% учебников передали в библиотеку. Сколько учебников передали в библиотеку?»
| 1 способ записи решения | 2 способ записи решения |
1) Чему равен 1% от числа 700 учебников? 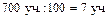 2) Сколько учебников передали в библиотеку? 2) Сколько учебников передали в библиотеку? 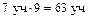 Ответ. 63 учебника передали в библиотеку. Ответ. 63 учебника передали в библиотеку. | 1) Сколько учебников передали в библиотеку? 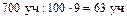 Ответ. 63 учебника передали в библиотеку. Ответ. 63 учебника передали в библиотеку. |
Полезно формулировки некоторых задач предлагать в развернутом виде, т.е. к рассматриваемому в условии сюжету ставить не один, а несколько последовательных вопросов. Это привлекает внимание учащихся к тому, какую информацию можно извлечь из ситуации с процентами. Например: «В магазине было 500 кг моркови. Продали 60% моркови. Сколько килограммов моркови продали? Сколько процентов всей моркови осталось в магазине? Сколько килограммов моркови осталось в магазине?» Еще один пример: «В кассе профкома было 9000 р. На оплату проездных билетов израсходовали 80% этой суммы. Какие вопросы можно поставить к задаче? Ответьте на них».
Также необходимо познакомить учащихся с формой неявного использования процентов, типичной для средств массовой информации, например: «Из каждых 100 новорожденных 49 – девочки».
Часто встречаются задачи, в которых нужно вычислить число процентов, превышающих 100%. Эти задачи имеют большое жизненно-практическое значение и часто встречаются.
Например: «Норма выработки рабочего – 400 деталей за смену. Он выполнил норму на 115%. Сколько деталей он сделал?»
Находим 115 % от 400. 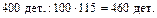
Ответ. Рабочий сделал за смену 460 деталей.
Задачу можно решить и другим способом. Рассуждаем так: 400 деталей – это 100%. Рабочий выполнил норму на 115%, т.е. перевыполнил план на 15% (115% – 100% = 15%). Найдем, сколько деталей рабочий сделал сверх плана. Надо найти 15% от 400 деталей. 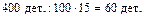 Далее узнаем, сколько деталей сделал рабочий за смену: 400 дет. + 60 дет. = 460 дет.
Далее узнаем, сколько деталей сделал рабочий за смену: 400 дет. + 60 дет. = 460 дет.
Ответ. Рабочий сделал за смену 460 деталей.
Задачи на нахождение 1 % от числа и на нахождение нескольких процентов от числа необходимо постоянно сопоставлять, находить черты сходства и различия.
Задачи на нахождение числа по одному проценту обратны задачам на нахождение 1% и нескольких процентов от числа. Поэтому, нужно сначала рассмотреть прямую задачу, решить ее, а потом из нее образовать обратную ей задачу, решить ее и сопоставить решение прямой и обратной задач.
Прямая задача: «В саду посадили 200 саженцев фруктовых деревьев. 1% саженцев погиб. Сколько саженцев фруктовых деревьев погибло?»
1 % от 200 – это 200 : 100 = 2 (саж.).
Обратная задача: «В саду посадили саженцы фруктовых деревьев. 2 саженца погибло, что составляет 1% от всех посаженных деревьев. Сколько саженцев фруктовых деревьев посадили в саду?»
Рассуждение проводим так: «2 саженца – это 1% всех деревьев, а все саженцы составляют 100%, т.е. их число в 100 раз больше 2, поэтому нужно 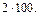 Следовательно, если 1% составляет 2 саженца, то 100% составляет
Следовательно, если 1% составляет 2 саженца, то 100% составляет 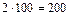 (саженцев)».
(саженцев)».
Решив еще несколько аналогичных задач и примеров на нахождение числа по одному проценту и сопоставив их с прямыми задачами и примерами, можно подвести учащихся к выводу: «Чтобы найти число по 1%, нужно это число умножить на 100».
Одна из особенностей вычислительной линии курса состоит в формировании умений выполнять прикидку или оценку результата вычисления. При изучении процентов учащимся предлагаются задачи из повседневной практики, в которых требуется найти приближенно с помощью прикидки процент от заданной величины. Для этого достаточно заменить данные другими числами, близкими к ним и удобными для расчетов. Так, если требуется прикинуть, чему равны 19% от какой-либо величины, то находят 20% этой величины, т.е. ее пятую часть. Или: «Перед Новым годом магазин снизил цены на товары на 25%. На сколько примерно рублей понизилась цена товара, если до снижения она составляла 799 руб.? 1980 руб.? 9880 руб.? 11890 руб.?».
При обучении учащихся классов КРО полезно использовать карточки для коррекции знаний (Г.Г. Левитас). Карточка для коррекции знаний состоит из трех частей: инструкция (формулировка правила); образец применения инструкции; три раздела заданий для учащихся. Карточки предназначены для дополнительных занятий с учащимися (в классе, на внеклассном коррекционно-развивающем занятии или дома). Если ученик на таком занятии правильно выполнил первый из трех разделов заданий, этого достаточно. Если же он не смог этого сделать, то учитель должен объяснить ему материал и дать задание из следующего раздела. Если и эти задания ученик не сможет выполнить, объяснения продолжаются и решаются остальные задания.
Приведем пример карточки для коррекции знаний то теме: «Нахождение процентов от числа».
| ПРАВИЛО | ОБРАЗЕЦ | ЗАДАНИЯ |
| 100% – это данное число. Найди 1% от данного числа. Найди нужное количество процентов от данного числа. | Найти 3% от 1500. Решение: Чему равен 1% от числа 1500? 1500 : 100 = 15. Чему равны 3% от числа 1500? 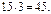 Ответ: 45. Краткая запись: Ответ: 45. Краткая запись: 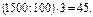 | Найти 2% от 800. Найти 6% от 3 кг. Прибор стоимостью 3000 руб. подешевел на 29%. На сколько рублей подешевел прибор? Что больше, 40% от 30 или 30% от 40? |
| Найти 4% от 1200. Найти 8% от 7 км. В городе было 4 млн. жителей; за 10 лет население выросло на 17%. Сколько теперь жителей в городе? Что больше, 41% от 53 или 53% от 41? | ||
| Найти 5% от 4100. Найти 9% от 1 часа. Вклад в 3000 долларов за год увеличился на 6%. Чему теперь равен вклад? Что больше, 51% от 47 или 52% от 48? |
Задания
1. Разработайте методику ознакомления учащихся 5 (6) класса КРО с одной из выбранных вами тем курса математики.
2. Ознакомьтесь с содержанием книг: [7; 9; 15; 26; 28]. Составьте фрагмент плана-конспекта урока математики в 5 (6) классе с использованием дидактической игры. Поясните коррекционно-развивающие возможности разработанной игры.
3. Подготовьте комплект карточек для коррекции знаний по курсу математики 5 (6) класса.
ГЛАВА 9. ИЗБРАННЫЕ ВОПРОСЫ МЕТОДИКИ коррекционно-развивающего ОБУЧЕНИЯ АЛГЕБРЕ в основной школе.
