Тема 3: «Дифференциальное исчисление функции нескольких переменных»
Пример 3.1.
Найти все частные производные 1-го порядка: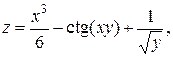 
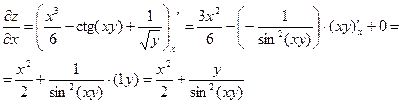
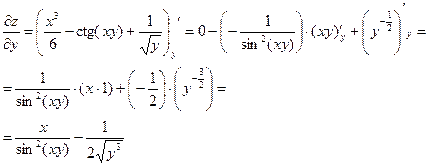Пример 3.2.
Найти все частные производные 1-го порядка
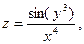
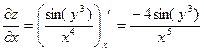
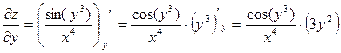
Пример 3.3.
Найти все частные производные 1-го порядка
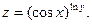
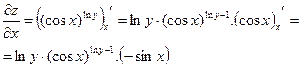
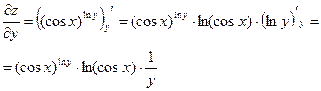
Пример 3.4.
Найти все частные производные 2-го порядка
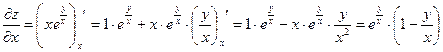
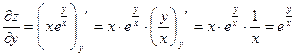
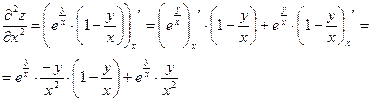
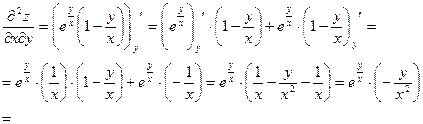
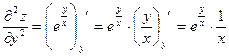
Пример 3.5.
Дана функция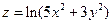 
, точка A(1; 1) и вектор 
.
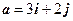Найти: a)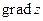 
в точке A; б) производную в точке A по направлению вектора a.
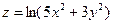
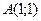
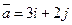
Найдем частные производные данной функции
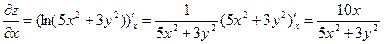
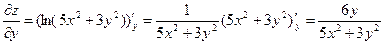
Подставим координаты точки А в данные частные производные.
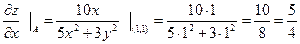
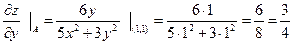
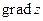в точке A
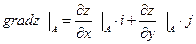
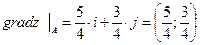
Определим направляющие косинусы для вектора а
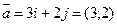
Для этого найдем длину вектора
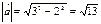
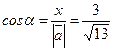
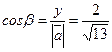
Найдем производную по направлению
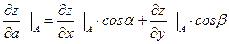
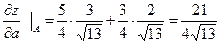
Пример 3.6.
Докажите, что функция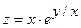 
удовлетворяет уравнению 
.
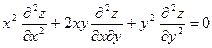Решение:
Найдем частные производные данной функции
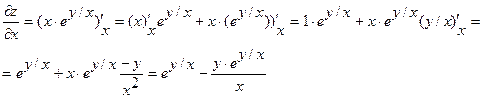
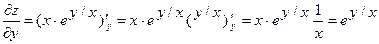
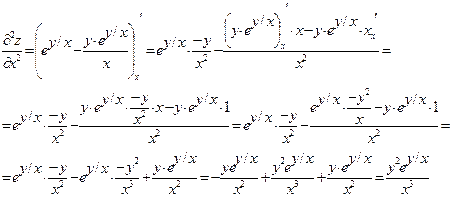
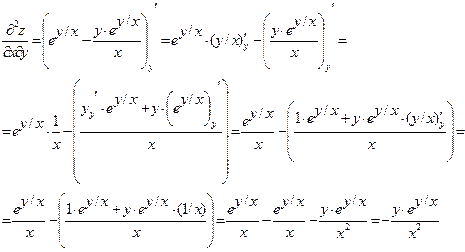
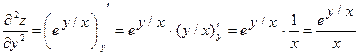
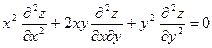
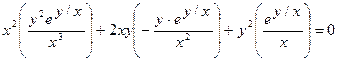
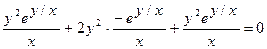
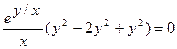
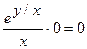
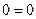
Пример 3.7.
Производственная деятельность фирмы описывается функцией Кобба-Дугласа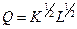 
, где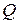 
- величина выпуска продукции, 
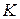- число единиц оборудования (капитал) и 
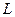- численность работающих (труд).
1) Составьте функцию издержек фирмы, если стоимость ед. фактора 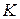равна 4 ден.ед., а стоимость ед. фактора 
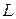равна 1 ден.ед.
2) Решите задачу определения максимального выпуска продукции, который может обеспечить фирма, полностью истратив все средства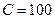 
ден.ед.
Решение:
Функция издержек фирмы
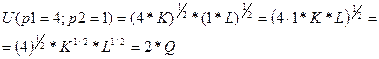ден. ед.
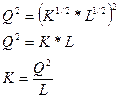
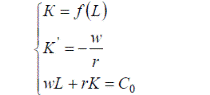
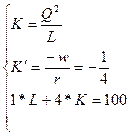
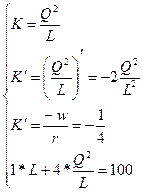
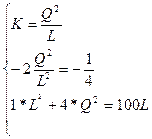
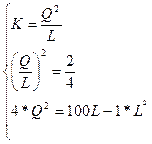
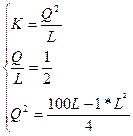
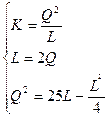
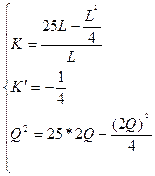
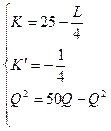
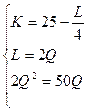
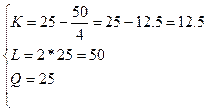
Изокванта для выпуска продукции объемом Q (4, 1)=2
 |
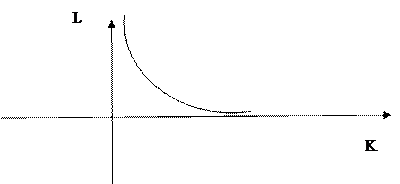К= 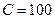ден.ед.
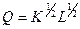
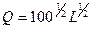
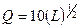
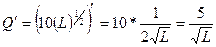
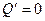
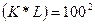
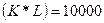
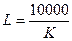
| K | ||||
| L |
Пример 3.8.
Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид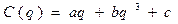 
.
a=15; b=0,009; c=100; p=85.
1) выполнить полное исследование функции зависимости прибыли фирмы П от объема производства q построить ее график;
2) найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль.
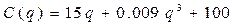
Прибыль= доход- издержки
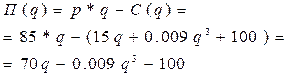
Общая схема исследования:
1. Область определения
2. Точки пересечения с осями координат
3. Четность-нечетность, периодичность.
4. Точки экстремума, промежутки возрастания, убывания функции.
5. Точки перегиба, промежутки выпуклости, вогнутости.
6. Асимптоты вертикальные и наклонные.
7. График.
1) Область определения
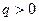
Д(q)=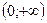 
2) Точки пересечения с осями координат
С ось ох =>у=0
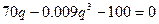
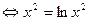нет корней
Нет точек пересечения с осями координат
3)Четность-нечетность, периодичность
Д(q)=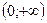
Так как график несимметричен относительно оси оу и начала координат, нечетная и не нечетная
Функция не содержит тригонометрических выражений - не является периодической.
4)Точки экстремума, промежутки возрастания, убывания.
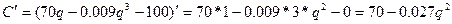
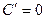
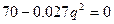
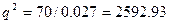
q=50.92- точка экстремума
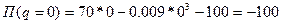убыток
| q | (0;50,92) | 50,92 | (50,92;  ) | |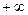
 | + | - | ||
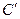| C | -100 | возрастает | 2275,3 | убывает |
5)Точки перегиба, промежутки выпуклости, вогнутости
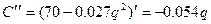
| q | | |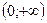
| | - | |
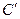| C | -100 | выпукла |
6) Асимптоты
У=кх+в
|
| |
|
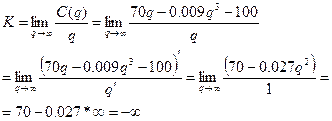
П=2275,3 прибыль