Метод хорд (метод пропорциональных частей)

Для нахождения корня 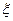уравнения 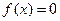, лежащего на заданном отрезке и удовлетворяющего условию имеется более быстрый способ.

Пусть . Заменим кривую на участке хордой, проходящей через точки

Из аналогичной геометрии мы знаем уравнение прямой проходящей через

точки : . У нас (см. рис. 13.8)

.

Точка пересечения хорды с кривой с осью имеет координаты

.

Подставим их в уравнение хорды при .

. (14.10)

Применяя этот метод к отрезку , получаем формулу

Многократное повторение приема приводит к итерационной формуле

Следует обратить внимание на то, что здесь неподвижен конец , а левые концы отрезков образуют ограниченную монотонно возрастающую последовательность

.

В случае же, когда неподвижен конец , последовательные приближения

образуют монотонно убывающую последовательность.

Сами приближения имеют вид

Т.е. итерационная формула сохраняет симметричный относительно неподвижного конца вид.

Существует такое правило:

1) неподвижен тот конец, для которого знак функции совпадает

со знаком ее второй производной ;

2) последовательные приближения 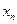лежат по ту сторону корня ,

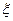где функция имеет знак, противоположный знак ее второй производной .

(Из математического анализа вспоминаем, что если , то функция обращена в точке 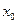выпуклостью вниз, если - то выпуклостью вверх).

Для оценки погрешности метода хорд можно воспользоваться формулой (14.6)

, где .

Можно привести еще одну оценку погрешности метода хорд:

.

Следовательно, как только будет обнаружено, что

< ,

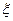где 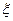- заданная предельная абсолютная погрешность, то гарантировано, что

< .

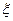Пример. Найти положительный корень уравнения

с точностью до 0,002.

Решение.

1). Прежде всего, отделим корень.

.

Видим, что 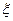(1;2).

2). Для уменьшения интервала разделим его пополам. Точка деления

Так как , окончательно выбираем интервал .

3). Находим . Видим, что вторая производная больше нуля при любом х, принадлежащем отрезку .

Условие выполняется для

Поэтому принимаем , . Используем формулу

.

4). Последовательно применяем эту формулу:

,

;

Так как ,

то .

Таким образом, где <

(Точный корень решаемого уравнения

Метод Ньютона (метод касательных).

Пусть корень 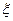уравнения отделен на ;

и непрерывны и сохраняют определенные знаки на .

Выберем, например, , для которого выполняется >0.

Проведем касательную к кривой в точке . Ее уравнение:

, где - угловой коэффициент прямой в точке ,

. Отсюда имеем . Теперь легко находится точка пересечения касательной с осью так как .

или .

Повторяя подобные рассуждения для точки , получаем второе приближение

.

Проделав такую операцию n раз, получим рекуррентную формулу

(14.11)

Для метода Ньютона также справедливо правило:

в качестве исходной точки выбирается тот конец интервала которому отвечает ордината того же знака, что и знак т.е.

Для оценки погрешности приближения можно воспользоваться общей формулой: (14.12)

С помощью формул (14.12) и ряда Тейлора относительно просто доказывается следующее неравенство:

. (14.13)

Формула (14.13) показывает быструю сходимость процесса Ньютона, если

приближение таково, что q .

В частности, если и то из формулы (14.13) получаем , т.е. в этом случае, когда имело верных десятичных знаков после запятой, следующее ее приближение будет иметь по крайней мере верных знаков. Иными словами число верных знаков после запятой искомого корня 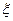удваивается на каждом шаге.

Пример. Вычислить методом Ньютона (касательных) отрицательный корень уравнения с пятью верными знаками.

Решение1). Отделение корня. Найдем значения

при .

.

Значит .

Сузим найденный интервал. Наудачу найдем

при

Т.к. мы нашли более узкий интервал смены знаков, примем

2). Определим производные функции в интервале .

Очевидно, что для

Условию удовлетворяет значение Следовательно, за

примем . - начальное (нулевое) приближение. Последующие приближения вычисляем по след. схеме:

	-11		-5183	0,7
	-10,3	134,3	-4234	0,03
	-10,27	37,8	-4196	0,009
	-10,261	0,2	-	-

Из таблицы видно, что уже при мы имеем в наличии пятый знак. Поэтому здесь уже достаточно проверить знак значения при

Проверка показывает, что Следовательно и любое из этих чисел даёт искомое приближение.