Основное уравнение конвективного теплообмена

Процесс переноса тепловой энергии от движущейся жидкости или газа к твердой стенке (или обратно) называется конвективным теплообменом или теплоотдачей.

Этот процесс включает две стадии и два вида переноса тепловой энергии:

– перенос тепловой энергии конвекцией в объеме жидкости или газа;

– перенос тепловой энергии теплопроводностью в тонком малоподвижном слое жидкости или газа, непосредственно прилегающем к твердой стенке и называемом пограничным слоем или ламинарным подслоем;

– передача тепла теплопроводностью при непосредственном соприкосновении частиц жидкости или газа с частицами твердой стенки непосредственно на границе твердой поверхности.

Как было показано выше (глава 8), конвективный перенос тепла протекает с большей интенсивностью и поэтому стадией, ограничивающей интенсивность процесса конвективного теплообмена, является теплопроводность в пограничном слое.

Так как толщина пограничного слоя исчезающее мала по сравнению с размерами стенки, то, в первом приближении, его можно считать плоской стенкой из жидкости со средней толщиной 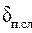и применить к ней уравнение теплопроводности через плоскую стенку (9.6) при t_ж - t_ст в виде

.

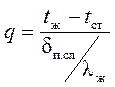(2.1)

Исходя из приведенных положений получено основное уравнение конвективного теплообмена, называемое уравнением Ньютона-Рихмана:

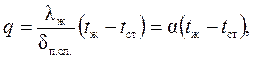(2.2)

где 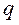– удельный тепловой поток при конвективном теплообмене, ;

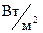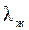– коэффициент теплопроводности жидкости (газа) в пограничном слое, ;

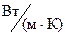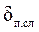– толщина пограничного слоя жидкости (газа), прилегающего к поверхности теплообмена, м;

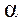– коэффициент теплоотдачи, характеризующий условия теплообмена между жидкостью и твердой стенкой, .

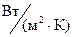Коэффициент теплоотдачи 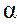есть основная характеристика процесса конвективного теплообмена и является сложной функцией большого количества независимых величин, характеризующих явление.

В частности, коэффициент теплоотдачи зависит от следующих групп параметров, характеризующих процесс конвективного теплообмена:

– величины, характеризующие режим движения жидкости относительно твердой поверхности (скорость, направление потока, движущие силы процесса и др.), в зависимости от которых режим движения может быть ламинарным или турбулентным, конвекция свободной и вынужденной и т. д., что в свою очередь, существенно влияет на толщину пограничного слоя и коэффициент теплоотдачи;

– величины, характеризующие физическое состояние жидкости (плотность, теплоемкость, вязкость, коэффициент теплопроводности, коэффициент объемного расширения и др.), от которых зависят процессы переноса тепловой энергии, формирование режима движения и т. д.;

– величины, характеризующие твердую поверхность (геометрические размеры, состояние и форма поверхности, положение поверхности по отношению поля силы тяжести и др.), от которых, так же, зависят характеристики процессов переноса тепла и режим движения жидкости;

– величины, характеризующие температурные условия процесса (температура жидкости и стенки, температурный напор и др.), определяющие интенсивность конвективного теплообмена.

Из-за сложности математического описания процесса конвективного теплообмена точное аналитическое решение системы дифференциальных уравнений конвективного теплообмена и условий однозначности явления в настоящее время не найдено. Частные решения, полученные путем внесения существенных упрощений в описание явления, дают значительные погрешности по сравнению с опытом.

Поэтому в настоящее время коэффициент теплоотдачи определяют, в основном, экспериментальным путем, что иногда невозможно, вследствие значительных технических трудностей (большие размеры объекта исследования, техническая невозможность воспроизведения условий и места теплообмена и т. д.). Поэтому, на практике для описания сложных процессов теплообмена используют методы теории подобия.