Операции над вещественными и целыми величинами
Когда аргументы двуместной операции имеют разные типы (один вещественный, другой целый), результат операции будет вещественным. Например, Х+I; A-I; 2**Х; A/I; I/A; A**N; 2**0.25 результаты операций будут вещественными. В большинстве случаев в процессе вычислений целая величина преобразуется к равной ей вещественной величине, после чего для получения результата используется вещественная арифметика. Целый результат дают лишь выражения, состоящие исключительно из целых величин. При записи целой константы в выражение смешанного типа предпочтительнее писать эквивалентное ей вещественное число. Так, выражение 1/Х лучше записать 1./Х Это избавит ЭВМ от преобразования целого числа 1 в вещественное 1.
Особенности целочисленного деления могут привести к неожиданным результатам при вычислении значений выражений смешанного типа. Рассмотрим математически тождественные выражения: A+L/M*B и A+B*L/M Если А = 1.1, L = 2, М = 3 и В = 3.0, то, применяя вышесказанные правила, получаем:
A + L / M * B = A + 2/3 * В = А + 0 * 3.0 = 1.1 + 0.0 = 1.1;
А + В * L / М = А + 3.0 * 2 / М = А + 6.0 / 3 = 1.1 + 2.0 = 3.1.
1.1.7 Возведение в вещественную степень ( 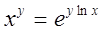 )
)
При возведении вещественного или целого числа в вещественную степень, например А**Х или I**Х, производятся следующие действия: логарифм A (или I) умножается на X, а затем берется экспонента от произведения EXP(LOG(A)*X), только при А > 0. Эта операция выполняется медленнее, чем другие операции, поэтому эффективнее записывать Х в квадрате как Х**2, (число 2 целое, без точки) а не Х**2.0. Напомним, что возведение в целую степень выполняется повторным умножением. Из сказанного следует, что в выражениях, подобных A**Х или I**Х, значение A или не может быть отрицательным, так как логарифм отрицательного числа не определен. С другой стороны, отрицательное число может быть возведено в целую степень без каких-либо проблем.
Возведение в отрицательную степень
Выражение 2**(-3) интерпретируется как 1/ (2**3). Последнее выражение предполагает целочисленное деление, поэтому в силу сказанного выше имеем 2**(-3) =0. В действительности любое ненулевое целое число, не равное 1 или -1, возведенное в отрицательную целую степень, даст в Фортране ноль. Отметим некоторые особенности действий в арифметических выражениях, несоблюдение которых является источником труднообнаруживаемых ошибок в программах:
1). Результат деления двух целых операндов всегда будет целым, а дробная часть отбрасывается. Поэтому значением выражений 13/4 и 15/4 будет 3, но 13./4.=3.25; 15./4.=3.75. Результатом вычисления выражения (4/5)*10 будет ноль. Отсюда видно, что дробный показатель степени следует записывать вещественным числом, но не целым. Например: Х1/3 следует записывать в виде X**(1/3.) или X**0.333 но не как X**(1/3), и не X**1/3.
2). Существует одно важное исключение из общего правила, касающееся возведения в целую степень. В выражении A**N степень не преобразуется к вещественному числу, и вычисления производятся умножением числа А на себя N раз. Таким образом, если N=3, то A**N эквивалентно выражению А*А*А
Корень квадратный
Функция"корень квадратный" (SQRT). Ее положительным аргументом (значением, из которого нужно извлечь корень квадратный) может быть любая вещественная константа, вещественная переменная, вещественное выражение либо функция. Приведем примеры: SQRT ( 2.0 ) SQRT (X ) SQRT ( A = B / C ) SQRT(SIN(X)) и т.п..
Необходимо отметить следующее:
а) аргументом функции SQRT не может быть целая константа, целая переменная или целое выражение. Например, выражение SQRT(2), приведет к ошибке;
б) квадратный корень из отрицательного числа не является вещественным числом, поэтому отрицательный аргумент функции SQRT недопустим;
в) значение функции SQRT(X) называется арифметическим квадратным корнем из числа X, это неотрицательное число, квадрат которого равен X;
г) корень квадратный из числа X можно также вычислить, возведя X в степень 0.5. Но намного эффективнее использовать функцию SQRT, так как возведение X в степень 0.5 т.е. (X**0.5) предполагает вычисление экспоненты EXP (LOG(X)* 0.5 ).
1.1.9.1 Таблицы с примерами записей выражений на Фортране:
Примеры записи арифметических выражений на Фортране Таблица №1
| ОПЕРАЦИЯ | СИМВОЛ | ПРИМЕРЫ |
| Сложение | + | A + B A +2.56 I+J K+1 |
| Перемена знака | - | -A -2.5 -1. -K |
| вычитание | - | A-B 2.5 – A I-J K-4 |
| Умножение | * | A * B A * 2.32 2 * I I * J |
| Деление | / | A/B SUM/3.0 I/2 J/K |
| Возведение в степень | ** | X**2 T**1.4 Y**X 2**K |
Последовательность выполнения операцийТаблица№2
| Операция | Уровень старшинства |
| ** | Уровень 1 |
| * и / | Уровень 2 |
| + и - | Уровень 3 |
Примеры алгебраических выражений и их записи на ФортранеТаблица №3
| Алгебраическое выражение | Арифметическое выражение Фортрана |
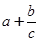 | A + B / C |
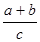 | (A + B) / C |
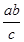 | A * B / C или A / C * B |
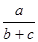 | A / ( B + C ) |
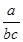 | A / ( B * C ) или A / B / C |
| b2 – 4ac | B **2 – 4.0 * A * C |
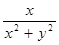 | X / (X ** 2 + Y ** 2) |
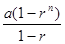 | A * (1.0 – R **N ) / ( 1.0 - R) |
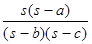 | S * ( S - A) / (( S – B ) * (S – C)) |
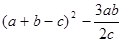 | (A + B - C) ** 2 – 3.0 * A * B / (2.0 * C) |
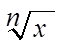 ; ; 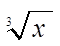 | X**(1 / n.) ; X**(1 / 3.) или х**0.33 |
Примечание: в выражении нельзя записать рядом две арифметические операции. Например, 2 в степени –3 должно быть записано как 2**(-3), а не 2** -3.
Операции отношения
A.GT.B (А больше чем В) >.AND. ^ - «И» объединение ( логич. умножение)
A.LT.B (А меньше чем В) < .NOT. ┐ - «НЕ» (логическое отрицание)
A.NE.B (А не равно В)…...≠ .OR . v - «ИЛИ» (логическое сложение)
A.GE.B (А больше или равно В) ≥A.EQ.B (А равно В) ═
A.LE.B (А меньше или равно В) ≤
Логические значения
.FALSE. - ложь .EQV. – эквивалентность
TRUE. - истина .NEQV. - неэквивалентность
В Фортране символ " - " ( подчеркивание ) считается буквой.
Примеры записи функций и выражений на ФортранеТаблица №4
| Математическая запись | Запись на Фортране |
| sin x | SIN (X) |
| cos x | COS (X) |
| tg x | TAN (X) |
| arccos x | ACOS(X) |
| arctg x | ATAN(X) |
| arcctg x | ACTAN(X) |
| ctg x | COTAN(X) |
| cth x | CTAN(H) |
| Sin2 x + cos x2 | Sin(x)**2 + cos (x**2) |
Продолжение Табл. №4 (Примеры записи и функций выражений)Таблица №5
| Имя | Определение | Аргумент | Значение |
| ABS(X) | Абсолютное значение │х │ | Вещест.Целый | Вщест.Целый |
| ACOS(X) | Знач. в рад. arccos x, -1≤ x ≤+1 | Вещественный | Вещественное |
| ASIN(X) | Знач. в рад. arcxin x, -1≤ x ≤ +1 | Вещественный | Вещественное |
| ATAN(X) | Знач. в рад. arctg x, -1≤ x ≤ +1 | Вещественный | Вещественное |
| COS(X) | cos x, x в радианах | Вещественный | Вещественное |
| COS(H) | ch x | Вещественный | Вещественное |
| EXP (X) | ex | Вещественный | Вещественное |
| INT | Приобразов. к целому значен. | Вещест.Целый | Целое. |
| ALOG(X) | ln x, x > 0 | Вещественный | Вещественное |
| ALOG10(x) | lg x, x > 0 | Вещественный | Вещественное |
| REAL | Приобразов. к вещест. значен. | Вещест.Целый | Вещественное |
| SIN(X) | sin x, x в радианах | Вещественный | Вещественное |
| SIN(H) | sh x | Вещественный | Вещественное |
| SQRT(X) | √x, x ≥ 0 | Вещественный | Вещественное |
| TAN(X) | tg x, x в радианах | Вещественный | Вещественное |
| TAN(H) | th x | Вещественный | Вещественное |
Специальные символы языка Фортран Таблица №6
