Создание блока передаточной функции с переменными коэффициентами
В стандартной библиотеке Simulink отсутствует блок передаточной функции, для которой можно было бы задавать коэффициенты числителя и знаменателя в виде входных векторов. Наличие такого блока позволило бы моделировать объекты, свойства которых меняются с течением времени. К таким объектам относятся и технологические объекты.
Создать такой блок можно используя следующую методику [3]. Передаточная функция:
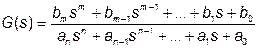
представляется в виде
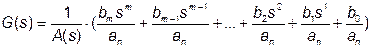 ,
,
где
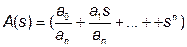 .
.
Затем численно решается дифференциальное уравнение, соответствующее передаточной функции
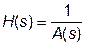 .
.
Для этого значения производных определяются на основе вычисления правых частей следующей системы нормальных дифференциальных уравнений:
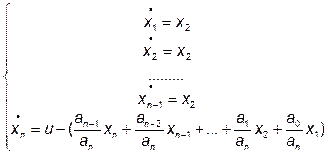
где
u - входное воздействие,
x1, x2, x3, …. xn, - переменные состояния.
Искомое решение (выходная переменная) находится следующим образом:
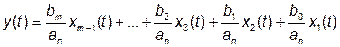
Для реализации изложенного алгоритма разработан блок Transfer Fcn (vp), схема и пиктограмма которого показаны на рис.2.1.
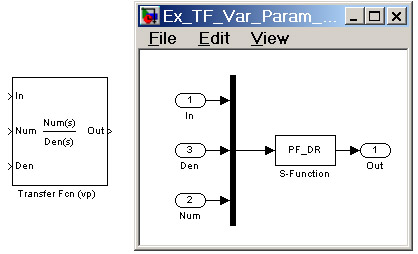
Рис. 2.1
Входное воздействие подается на входной порт In, а выходной сигнал снимается с порта Out. На вход Num должен быть подан вектор коэффициентов числителя, а на вход Den - вектор коэффициентов знаменателя.
Для создания блока Transfer Fcn (vp) необходимо в библиотеке Simulink взять блок «S-Function» и определить его параметры так, как показано на рисунке 2.2:
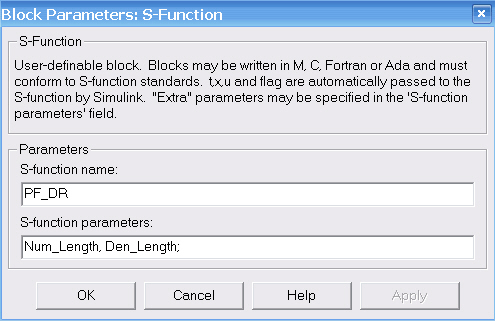
Рис. 2.2
Затем необходимо собрать схему, показанную на рис. 2.1 и объединить её в субсистему.
После создания субсистемы необходимо открыть для нее «Mask Editor» и прописать все необходимые параметры, так как показано на рис. 2.3а – 2.3с.
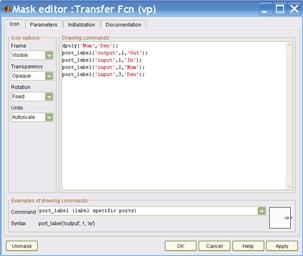
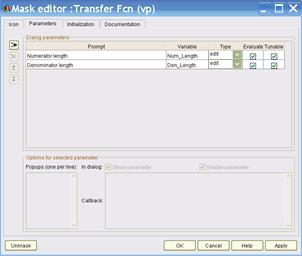
а) б)
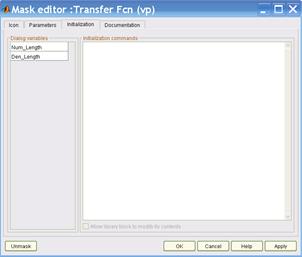
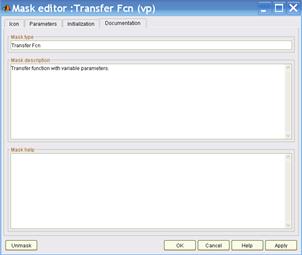
в) с)
Рис. 2.3
В окне задания параметров (рис. 2.4) необходимо указать размерность векторов коэффициентов числителя и знаменателя.
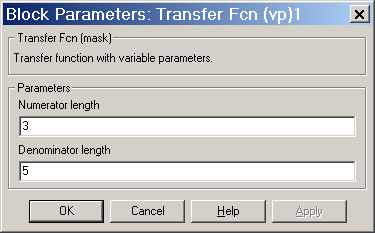
Рис. 2.4
Параметры блока: Numerator length: [Размерность вектора коэффициентов числителя]. Размерность вектора коэффициентов числителя не должна превышать размерность вектора коэффициентов знаменателя.
Denominator length: [Размерность вектора коэффициентов знаменателя].
Сам алгоритм расчета выходного сигнала блока реализован с помощью S-функции, текст которой с необходимыми комментариями приведен ниже.
function [sys,x0,str,ts] = PF_DR(t,x,u,flag,n_chisl,n_znam)
% Дробно-рациональная передаточная функция. Коэффициенты
% числителя и знаменателя передаются через вход S-функции
% В параметрах S-функции необходимо указать размерности векторов
% числителя (n_chisl) и знаменателя (n_znam)
% Определение максимальной размерности знаменателя:
if n_znam <=1
n_znam_max = 1;
else
n_znam_max = n_znam;
end
switch flag, % В зависимости от значения переменной flag происходит
% вызов того или иного метода:
%===============%
% Инициализация %
%===============%
case 0,
[sys,x0,str,ts] = mdlInitializeSizes(n_znam,n_znam_max,n_chisl);
dx1 = 0;
% Присвоение производной первой переменной состояния нулевого
% начального значения
set_param(gcb,'UserData',dx1);
% Запоминание значения dx1 в параметре UserData блока S-function
%====================%
% Расчет производных %
%====================%
case 1,
sys = mdlDerivatives(t,x,u,n_znam,n_znam_max,n_chisl);
dx1 = sys(n_znam-1); % Извлечение производной первой
% переменной состояния
set_param(gcb,'UserData',dx1);
% Запоминание значения dx1 в параметре UserData блока S-function
%===========================================%
% Расчет значений вектора выходных сигналов %
%===========================================%
case 3,
dx1 = get_param(gcb,'UserData');
% Присвоение значения dx1, извлеченного из параметра UserData
% блока S-function
sys = mdlOutputs(t,x,u,n_znam,n_chisl,dx1);
%=========================================%
% Неиспользуемые значения переменной flag %
%=========================================%
% В примере не используются методы для завершения работы S-функции,
% нет дискретных переменных состояния,
% поэтому значения переменной flag = 2, 4, 9 не используются.
% Результатом S-функции в этом случае является пустая матрица.
case { 2, 4, 9 }
sys=[];
%======================================%
% Неизвестное значение переменной flag %
%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% Окончание csfunc
%
%===============================================================%
% mdlInitializeSizes %
% Функция инициализации %
% Расчет начальных условий, значений вектора шагов модельного %
% времени,размерности матриц %
%===============================================================%
%
function [sys,x0,str,ts]=mdlInitializeSizes(n_znam,n_znam_max,n_chisl)
sizes = simsizes;
sizes.NumContStates = n_znam_max; % Число непрерывных переменных
% состояния.
sizes.NumDiscStates = 0; % Число дискретных переменных состояния.
sizes.NumOutputs = 1; % Число выходных переменных (размерность
% выходного вектора).
sizes.NumInputs = (1 + n_znam + n_chisl);
% Число входных переменных (размерность входного вектора).
sizes.DirFeedthrough = 1; % Прямой проход. Есть проход входного
% сигнала на выход
sizes.NumSampleTimes = 1; % Размерность вектора шагов модельного
% времени.
sys = simsizes(sizes);
x0 = zeros(n_znam_max,1); % Задание вектора начальных значений
% переменных состояния.
% Начальные условия нулевые, если порядок
% числителя меньше порядка знаменателя
str = []; % Параметр зарезервирован для будущего использования.
ts = [0 0];% Матрица из двух колонок, задающая шаг модельного
% времени и смещение.
% Окончание mdlInitializeSizes
%
%=============================================================%
% mdlDerivatives %
% Функция для расчета значений производных вектора состояния %
% непрерывной части системы %
%=============================================================%
%
function sys = mdlDerivatives(t,x,u,n_znam,n_znam_max,n_chisl);
[u_vh,a,b] = param(u,n_znam,n_chisl);
% Извлечение из входного сигнала входной переменной,
% а также векторов знаменателя и числителя
sys = zeros(n_znam_max,1);
if n_znam > 1
for k = 1:(n_znam - 2);
sys(k) = x(k+1);
end
s = 0;
for k = 1:(n_znam - 1);
s = s + (a(k)/a(n_znam))*x(k);
end
sys(n_znam-1) = u_vh - s; % Вычисление производных выходного
% сигнала
end
% Окончание mdlDerivatives
%
%========================================================%
% mdlOutputs %
% Функция для расчета значений вектора выходных сигналов %
%========================================================%
%
function sys=mdlOutputs(t,x,u,n_znam,n_chisl,dx1)
[u_vh,a,b] = param(u,n_znam,n_chisl);
% Извлечение из входного сигнала входной переменной
% и векторов знаменателя и числителя
x1=x;
x1(n_znam) = dx1;
sys = 0;
for k = 1: n_chisl;
sys = sys + b(k)/a(n_znam)*x1(k); % Вычисление выходного
% сигнала
end
if t == 0 % Вычисление выходного сигнала для момента времени t == 0
if n_chisl == n_znam
sys = u_vh*b(n_chisl)/a(n_znam);
% Если порядки числителя и знаменателя равны, то выходной сигнал
% равен входному, умноженному на отношение свободных членов
else
sys = 0;
% В противном случае выходной сигнал равен 0.
end
end
% Окончание mdlOutputs
function [u_vh,a,b] = param(u,n_znam,n_chisl);
% Функция извлечения из входного сигнала входной переменной
% и векторов знаменателя и числителя
u_vh = u(1); % Извлечение входного сигнала
% Извлечение вектора коэффициентов знаменателя:
n = n_znam;
for k = 2:(2 + n_znam - 1);
a(n) = u(k);
n = n - 1;
end
% Извлечение вектора коэффициентов числителя:
n = n_chisl;
for k = (2 + n_znam):(2 + n_znam + n_chisl -1);
b(n) = u(k);
n = n - 1;
end
% Окончаниие функции param
На рис.2.5 показано сравнение работы нового блока со стандартным блоком Transfer Fcn. Как видно из графиков на рисунке, результаты полностью совпадают.
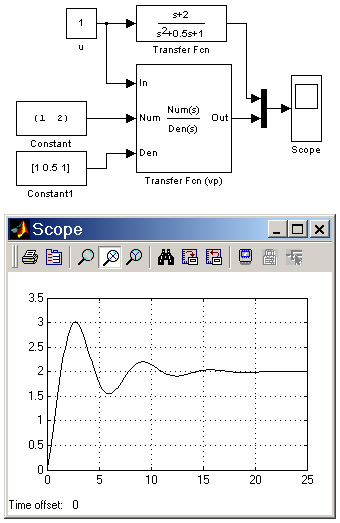
Рис. 2.5
В том случае, если коэффициенты числителя и знаменателя заданы в виде таблиц в функции какого-либо параметра, необходимо иметь также блок, обеспечивающий интерполяцию коэффициентов при изменении этого параметра. Такой блок может быть создан на основе S-функции с применением стандартной функции MATLAB interp1. Схема и пиктограмма блока интерполяции показаны на рис.2.6. Окно задания параметров показано на рис.2.7.
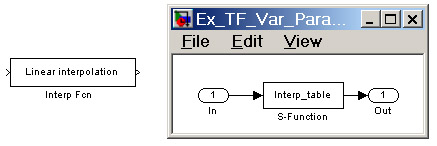
Рис. 2.6
Окно задания параметров:
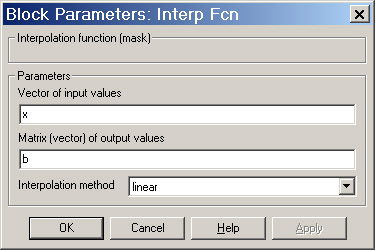
Рис. 2.7
Параметры блока:
Vector of input values: [Вектор входных значений]. Размерность вектора коэффициентов числителя не должна превышать размерность вектора коэффициентов знаменателя.
Matrix (vector) of output values: [Матрица или вектор выходных значений]. Каждая строка в матрице выходных значений соответствует новому набору коэффициентов.
Interpolation method: [Метод интерполяции]. Значение параметра выбирается из списка:
· linear - линейная интерполяция,
· cubic - кубическая интерполяция,
· spline - сплайн-интерполяция.
Сам алгоритм расчета выходного сигнала блока реализован с помощью S-функции, текст которой с необходимыми комментариями приведен ниже.
function [sys,x0,str,ts] = Interp_table(t,x,u,flag,x_vh,y_vh,method)
% Функция для интерполирования коэффициентов полиномов
% передаточной функции.
% x_vh - вектор аргумента
% y_vh - матрица значений табличной функции
% method - метод интерполяции
switch flag, % В зависимости от значения переменной flag
% происходит вызов того или иного метода:
%===============%
% Инициализация %
%===============%
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(y_vh);
%===========================================%
% Расчет значений вектора выходных сигналов %
%===========================================%
case 3,
sys=mdlOutputs(t,x,u,x_vh,y_vh,method);
%=========================================%
% Неиcпользуемые значения переменной flag %
%=========================================%
% В примере не используются методы для завершения работы S-функции,
% нет дискретных переменных состояния, нет вычисления производных,
% поэтому значения переменной flag = 1, 2, 4, 9 не используются.
% Результатом S-функции в этом случае является пустая матрица.
case {1, 2, 4, 9}
sys=[];
%======================================%
% Неизвестное значение переменной flag %
%======================================%
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
% Окончание csfunc
%
%===============================================================%
% mdlInitializeSizes %
% Функция инициализации %
% Расчет начальных условий, значений вектора шагов модельного %
% времени, размерности матриц %
%===============================================================%
%
function [sys,x0,str,ts]=mdlInitializeSizes(y_vh)
[size_x size_y] = size(y_vh);
sizes = simsizes;
sizes.NumContStates = 0; % Число непрерывных переменных состояния.
sizes.NumDiscStates = 0; % Число дискретных переменных состояния.
sizes.NumOutputs = size_y; % Число выходных переменных
% (размерность выходного вектора).
sizes.NumInputs = 1 ; % Число входных переменных
% (размерность входного вектора).
sizes.DirFeedthrough = 1; % Прямой проход. Есть проход входного
% сигнала на выход
sizes.NumSampleTimes = 1; % Размерность вектора шагов модельного времени.
sys = simsizes(sizes);
x0 = []; % Задание вектора начальных значений переменных состояния.
% Начальные условия нулевые
str = []; % Параметр зарезервирован для будущего использования.
ts = [0 0]; % Матрица из двух колонок, задающая шаг модельного
% времени и смещение.
% Окончание mdlInitializeSizes
%
%======================================================%
% mdlOutputs %
% Функция для расчета значений вектора выходных сигналов %
%======================================================%
%
function sys=mdlOutputs(t,x,u,x_vh,y_vh,method)
sys = interp1(x_vh,y_vh,u,method);
% Окончание mdlOutputs
На рис. 2.8 показана схема, в которой интерполяция коэффициентов передаточной функции производится с помощью разработанного блока Interp Fcn. Значения коэффициентов числителя и знаменателя считываются из файлов с помощью блока Load Num & Den. Схема выполняет расчет для любого значения переменной x, лежащего в пределах от 0 до 6.6.
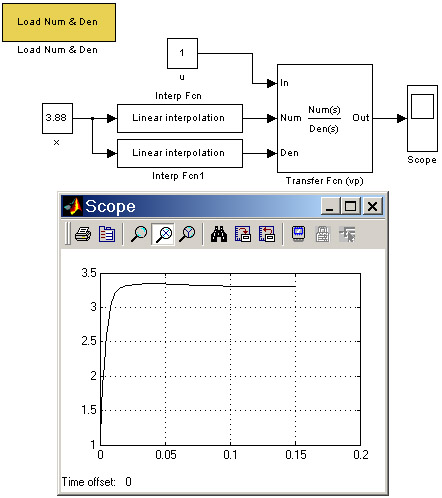
Рис. 2.8
Задание
1. Создание блока передаточной функции с переменными коэффициентами по методике изложенной выше.
2. В модели лабораторной работы 1 (рис 1.9) заменить передаточную функцию ДПТ на передаточную функцию, полученную в пункте 1. Исследовать полученную модель при изменении параметров во времени.
3. Сделать выводы.
Лабораторная работа № 3
Использование блока «Nonlinear Control Design Blockset» для настройки параметров промышленных регуляторов.
Цель работы
Настройки параметров промышленных регуляторов с использованием блока «Nonlinear Control Design Blockset»
