Усовершенствованный метод Эйлера

Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования –формулой трапеций.

Основная идея этого метода: вычисляемое по формуле (5) очередное значение 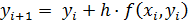будет точнее, если значение производной, то есть угловой коэффициент прямой замещающей интегральную кривую на отрезке 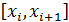будет вычисляться не по левому краю (то есть в точке 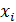), а по центру отрезка 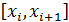. Но так как значение производной между точками 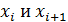не вычисляется, то перейдем к сдвоенным участкам 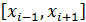центром, в которых является точка 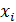, при этом уравнение прямой получает вид:

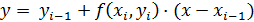(6)

А формула (5) получает вид

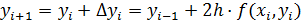(7)

Формула (7) применена только для 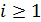, следовательно, значения 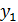по ней получить нельзя, поэтому 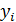находят по методу Эйлера, при этом для получения более точного результата поступают так: с начала по формуле (5) находят значение

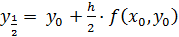(8)

В точке 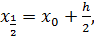а затем находится 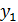по формуле (7) с шагом

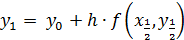(9)

После того как 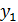найдено дальнейшие вычисления при 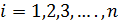производится по формуле (7)

….

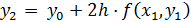Пример

В качестве примера проведем расчеты по формулам усовершенствованного методаЭйлера с шагом h=0,1 для задачи Коши .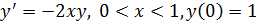

;

***

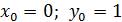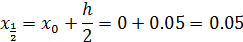
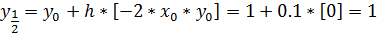
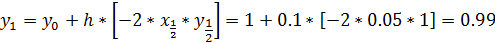
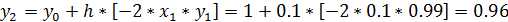
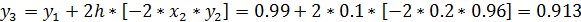
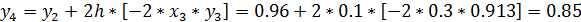
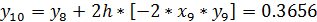
Модифицированный метод Эйлера

Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.

Прогноз:

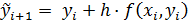(10)

Коррекция:

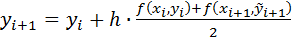(11)

Геометрически это означает, что с начало определяется направление интегральной кривой в исходной точке 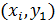и во вспомогательной точке 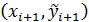, а в качестве окончательного направления берется среднее значение этих направлений.

Благодаря более точной формуле интегрирования, погрешность метода пропорциональна уже квадрату шага интегрирования.

Пример

В качестве примера проведем расчеты по формулам модифицированным методомЭйлера с шагом h=0,1 для задачи Коши .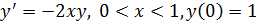

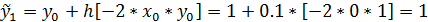
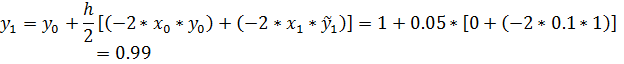
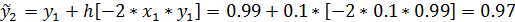
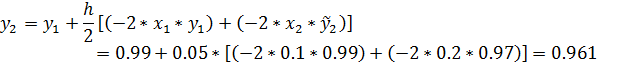
Таблица Решение уравнения модифицированным методами Эйлера

xi		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
yi		0.99	0.961	0.914	0.852	0.779	0.698	0.613	0.528	0.446	0.369

Точное решение имеет вид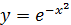

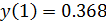
Метод Рунге-Кутты

Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка - широко используемого в вычислительной практике метода Рунге-Кутты.

В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [x_i+1 , x_i].

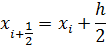
тогда можно определить так

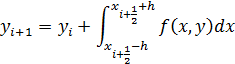
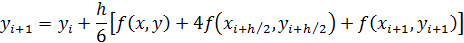
Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции y_i+h/2 и y_i+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений .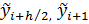

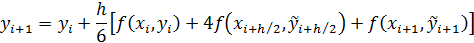
При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.

Алгоритм Рунге-Кутты четвертого порядка - (погрешность порядка h⁴):

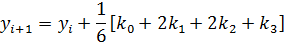
где

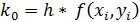
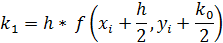
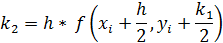
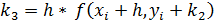
Алгоритм четвертого порядка требует на каждом шаге четырех вычислений функции соответственно, но является весьма точным.