Численное интегрирование. Рассмотрим способы приближенного вычисления определенных интегралов

Рассмотрим способы приближенного вычисления определенных интегралов

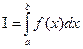, (13.1)

основанные на замене интеграла конечной суммой

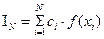. (13.2)

Приближенное равенство

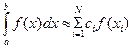
называется квадратурной формулой, а сумма вида (13.2) - квадратурной суммой. Точки 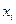называются узлами квадратурной формулы, числа 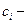коэффициентами (весами) квадратурной формулы.

Разность 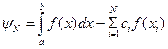называется погрешностью квадратурной формулы.

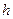Введем на равномерную сетку с шагом , т.е. множество точек

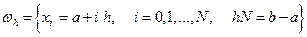
и представим интеграл (13.1) в виде суммы интегралов по частичным отрезкам:

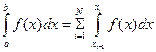. (13.3)

Для построения формулы численного интегрирования на всем отрезке

достаточно построить квадратурную формулу для интеграла

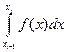(13.4)

на частичном отрезке 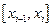и воспользоваться формулой (13.3).

Формула прямоугольников. Заменим интеграл (13.4) выражением

.

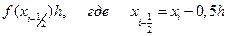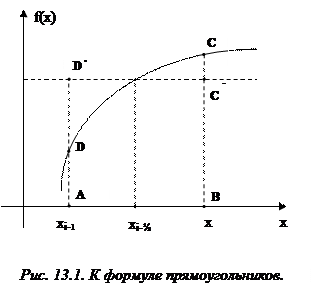Геометрически такая замена означает, что площадь криволинейной трапеции 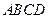заменяется площадью прямоугольника 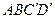. Тогда получим формулу

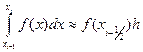, (13.5)

которая называется формулой прямоугольников на частичном отрезке .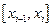

Погрешность формулы (13.5) определяется величиной

,

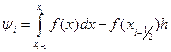которую можно оценить с помощью формулы Тейлора.

Запишем 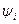в виде

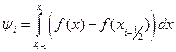(13.6)

и воспользуемся разложением относительно

,

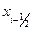
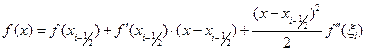где 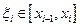. Подставляя данное разложение в (13.6), получаем:

.

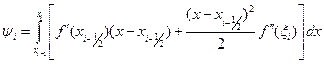Нетрудно убедиться в том, что ,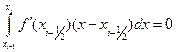

и тогда .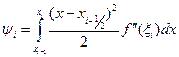

Обозначив 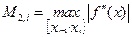, оценим :

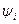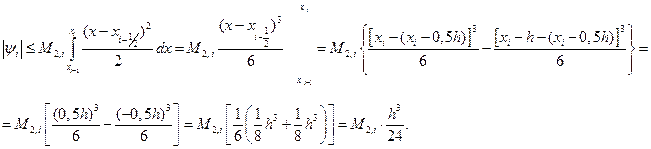
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

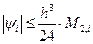, (13.7)

т. е. формула имеет погрешность .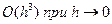

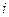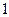Суммируя равенства (13.5) по от до 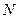, получаем составную формулу прямоугольников

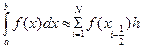. (13.8)

Погрешность этой формулы

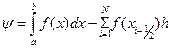
равна сумме погрешностей по всем частичным отрезкам,

.

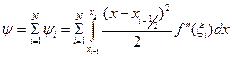Обозначая 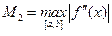, получим

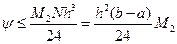, (13.9)

(т.к. 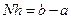), т.е. погрешность формулы прямоугольников на всем отрезке есть .

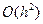В этом случае говорят, что формула имеет второй порядок точности.

Замечание. Формулы прямоугольников при ином расположении узлов, например, формулы

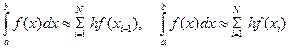
из-за нарушения симметрии имеют точность первого порядка, т.е. .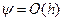

Формула трапеций. На частичном отрезке эта формула имеет вид

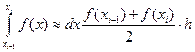. (13.10)

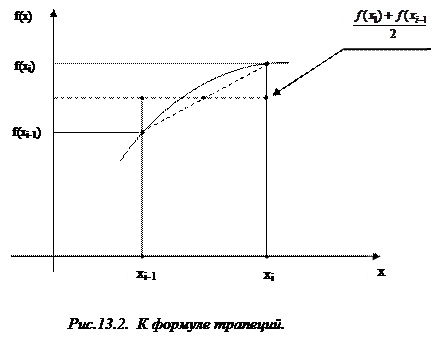Она получается путем замены подынтегральной функции интерполяционным многочленом первой степени, построенным по узлам 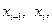т.е. функцией

.

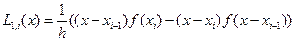Для оценки погрешности формулы трапеций воспользуемся оценкой погрешности приближения многочленом Лагранжа, т.е. (6.27).

.

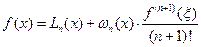Поэтому .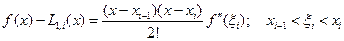

Следовательно, .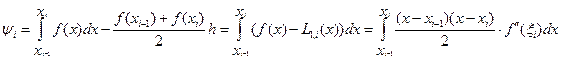

.

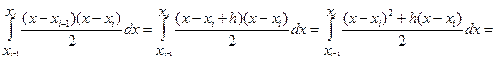
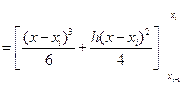
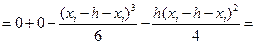
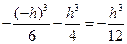Итак, 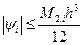, где 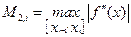. (13.11)

Составная формула трапеций имеет вид

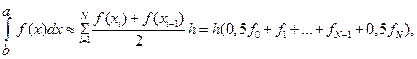(13.12)

где .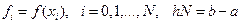

По аналогии с формулой (13.9) получается формула для оценки погрешности формулы трапеций

.

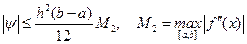Формула Симпсона.

При приближении интеграла 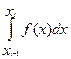заменим функцию параболой, проходящей через точки ,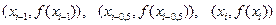

т.е. представим приближенно в виде

,

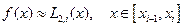где 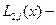интерполяционный многочлен Лагранжа второй степени

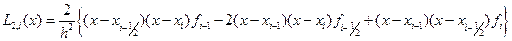. (13.13)

Проводя интегрирование, получим

=

.

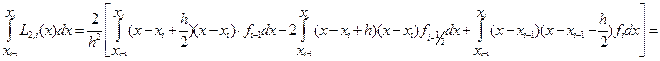
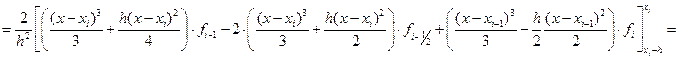
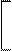
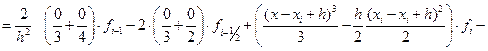
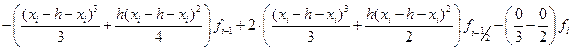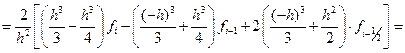
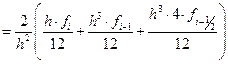
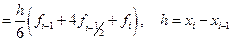Таким образом, приходим к приближенному равенству,

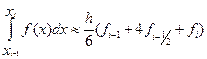, (13.14)

которое называется формулой Симпсона или формулой парабол.

На всем отрезке формула Симпсона имеет вид

.
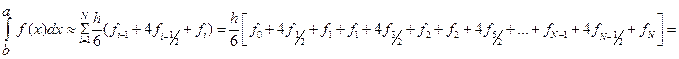
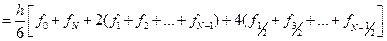