Обратные тригонометрические функции
Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными[источник?] к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1.
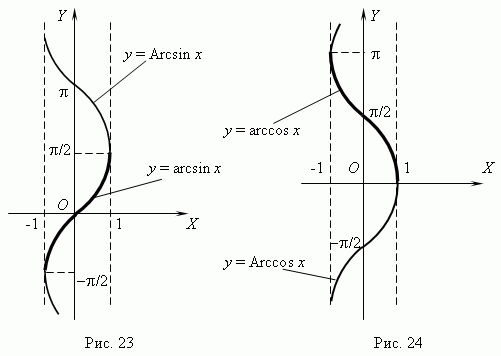
Функция arcsin.
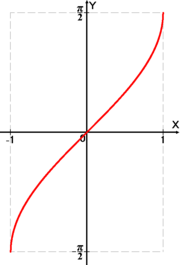
График функции y = arcsinx.
Арксинусом числа m называется такой угол x, для которого 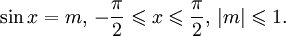
Свойства функции arcsin:
-
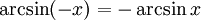 (функция является нечётной).
(функция является нечётной). -
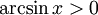 при
при 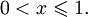
-
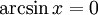 при x = 0.
при x = 0. -
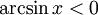 при
при 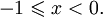
-
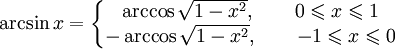
-
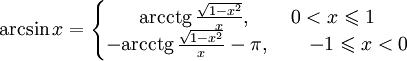
Функция arcos.
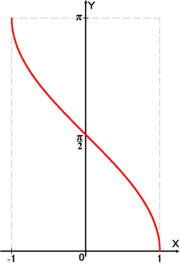
График функции y = arccosx.
Арккосинусом числа m называется такой угол x, для которого 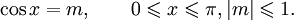
Свойства функции arcos:
- arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
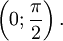
- arccosx > 0 при
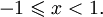
- arccosx = 0 при x = 1.
-
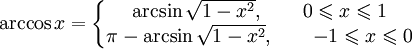
-
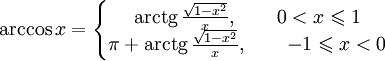
Формула выше, по-моему, не очень верна [xmode]
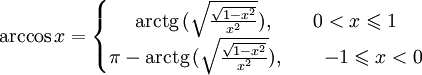
Функция arctg.
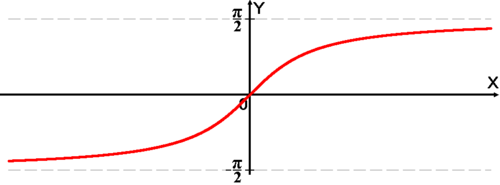
График функции 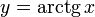 .
.
Арктангенсом числа m называется такой угол x, для которого 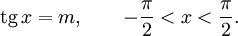
Свойства функции arctg:
-
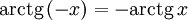 (функция нечётная).
(функция нечётная). -
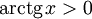 при x > 0.
при x > 0. -
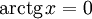 при x = 0.
при x = 0. -
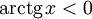 при x < 0.
при x < 0. -
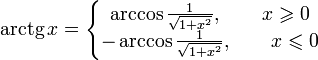
-
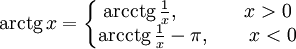
Функция arcctg.
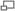
График функции y=arcctg x
Арккотангенсом числа m называется такой угол x, для которого 
Свойства функции arcctg:
-
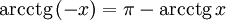 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 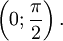
-
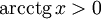 при любых x.
при любых x. -
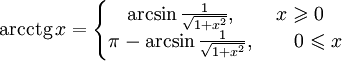
Использование в геометрии:
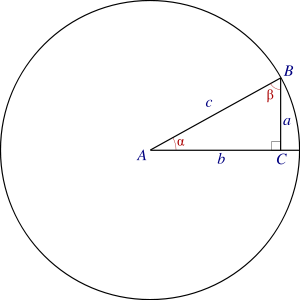
Прямоугольный треугольник ABC
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол:
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a) .
III. Заключение.
Изучением функций, в частности, элементарных, занимались многие ученые-математики на протяжении всего развития функций, но и сейчас нельзя сказать, что они полностью и подробно изучены, и я попыталась расширить кругозор своих знаний об элементарных функциях, я узнал какие функции можно получить из основных элементарных функций, и какими свойствами они обладают.
IV. Список литературы.
