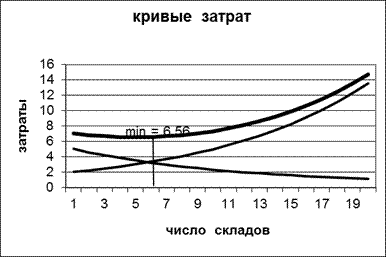
Пример выполнения лабораторной работы на Пэвм
Исходные данные:
1. y = 0,5 + 5 * exp(-x/10)
2. Y = 5 * exp(x/10-1)
Работа выполняется в программе EXCEL. Для этого в программу вводятся формулы двух зависимостей и число складов (от 1 до 20).
В программу закладывают вычерчивание графиков кривых.
Затем работу можно проводить по двум вариантам:
1. Распечатать две кривые на принтере, построить суммарную кривую вручную. Найти оптимальный результат.
2. В программе EXCEL построить суммарную кривую в уже имеющемся вышеуказанном графике и вывести всё на печать. Найти оптимальный результат.
На рисунке 4.3 приведен второй вариант выполнения задания.
|
Рисунок 5.3 – Пример выполнения лабораторной работы № 5
Выводы к работе
Студенты должны сделать вывод по конкретному заданию, т.е. при каком числе складов затраты на транспортирование и на складирование будут оптимальными.
Оформление
Работа оформляется в следующей последовательности:
1. Цель работы.
2. Классификация понятия «логистика». Выбор оптимального решения при решении функциональных задач.
3. График выбора числа складов по заданным исходным данным.
4. Вывод.
5.8 Контрольные вопросы
1. По каким основным признакам классифицируется понятие «логистика»?
2. Назвать типы понятия логистики по их основным признакам и объяснить их смысл.
3. Какая зависимость в ЛС существует между затратами на транспортирование, затратами на складирование и числом складов для хранения изделий или сырья.
Лабораторная работа № 6.
Управление запасами
Цель: расчёт параметров заказа – EOQ (Economic order quantity) – модели экономичного размера заказа.
Теоретические положения
Среди огромного разнообразия методов и моделей управления запасами на практике применяется достаточно ограниченное количество, в основном те модели, которые позволяют получить относительно простые способы регулирования параметров заказа, поставок и уровней запасов на складе, а также не требуют больших объёмов исходной информации и сложных методов контроля.
В вышеприведенном примере приведена одна из распространённых на практике оптимизационных моделей управления запасами – модель экономического размера заказа. Эта модель предполагает следующие допущения:
- спрос (расход) является непрерывным, а интенсивность спроса – постоянна;
- период между двумя смежными заказами (поставками) постоянна;
- спрос удовлетворяется полностью и мгновенно;
- транзитный и страховой запасы отсутствуют;
- ёмкость склада не ограничена;
- затраты на выполнение заказа и цена поставляемой продукции в течении планового периода постоянные;
- затраты на поддержание запаса единицы продукции в течение единицы времени постоянные.
Задание на выполнение лабораторной работы.
Исходные данные по вариантам приведены в табл. 6.1.
Таблица 6.1 – Исходные данные
| Параметры № варианта | D, ед. | C0 , ден.ед. | I, % | C, ден.ед. | 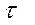 , нед. , нед. | Приме-чание |
| 60,8 | 22,0 | 29,3 | 1,5 | |||
| 99,1 | 15,0 | 21,0 | 1,0 | |||
| 72,9 | 16,0 | 23,5 | 1,3 | |||
| 17,5 | 24,8 | 1,5 | ||||
| 94,2 | 22,1 | 1,4 | ||||
| 56,7 | 24,8 | 0,9 | ||||
| 81,1 | 18,9 | 27,2 | 0,89 | |||
| 64,1 | 31,8 | 15,9 | ||||
| 135,8 | 24,1 | 18,2 | 0,95 | |||
| 17,5 | 17,1 | 1,4 | ||||
| 26,0 | 29,4 | 1,3 | ||||
| 18,3 | 29,4 | 1,1 | ||||
| 175,8 | 17,2 | 27,5 | 0,87 | |||
| 38,7 | 21,0 | 21,5 | 0,89 | |||
| 154,2 | 23,5 | 16,8 | 1,13 | |||
| 87,5 | 24,8 | 31,5 | 1,0 | |||
| 81,9 | 22,1 | 38,1 | 1,5 | |||
| 54,2 | 17,6 | 29,1 | 1,4 | |||
| 25,1 | 24,8 | 0,9 | ||||
| 29,1 | 27,2 | 0,89 | ||||
| 24,8 | 15,9 | |||||
| 27,2 | 18,2 | 0,95 | ||||
| 15,9 | 17,1 | 1,4 | ||||
| 84,9 | 18,2 | 18,3 | 1,3 | |||
| 17,1 | 17,2 | 1,1 | ||||
| 142,8 | 29,4 | 21,0 | 0,87 | |||
| 95,2 | 27,5 | 23,5 | 1,4 | |||
| 78,0 | 21,5 | 16,0 | 1,3 | |||
| 127,5 | 16,8 | 17,5 | 1,1 | |||
| 113,9 | 31,5 | 0,87 | ||||
| 38,1 | 0,89 | |||||
| 57,9 | 16,5 | 18,9 | 1,13 | |||
| 21,8 | 31,8 | 1,5 |
Необходимо рассчитать параметры системы управления запасами с фиксированным интервалом времени между заказами и построить график моделирования её работы. Сделать вывод.
Пример выполнения.
Покажем порядок расчёта на примере исходных данных, приведенных в табл. 6.2.
Таблица 6.2 – пример исходных данных
| Параметры | D, ед. | C0 , ден.ед. | I, % | C, ден.ед. | 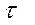 , нед. , нед. | |
| Величина | 60,8 | 22,0 | 29,3 | 1,5 |
где: D – годовая потребность в МП (спрос на ГП – готовую продукцию);
C0 –затраты на выполнение заказа, ден.ед.;
I – доля от цены, приходящаяся на затраты по поддержанию запасов, ден.ед.;
C – цена единицы продукции, хранимой на складе, ден.ед.;
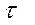 - величина времени запаздывания поставки.;
- величина времени запаздывания поставки.;
Q – средняя величина запаса, поддерживаемая на складе, ед.
Расчёт EOQ.
Для определения EOQ используем формулу:
EOQ = q = 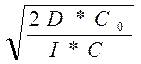 ; (6.1)
; (6.1)
EOQ = 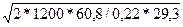 = 150,46 ед. = 151 ед.
= 150,46 ед. = 151 ед.
Таким образом, оптимальная величина заказа (партия поставки) будет равна 151 единице продукции. Оптимальное время между двумя смежными заказами будет равно:
T = q / D ; T = 150,46/1200 = 0,125383(3) года
или в неделях
T = 0,125383(3) * 52 = 6,5 недель.
Определяем оптимальное количество заказов за год:
N = D / q ; N = 1200 /0150,46 = 8 заказов.
Важное значение имеет определение момента заказа 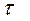 – точки заказа/перезаказа, т.е. достижение при расходовании запаса со склада такого уровня (Qз), когда необходимо делать заказ.
– точки заказа/перезаказа, т.е. достижение при расходовании запаса со склада такого уровня (Qз), когда необходимо делать заказ.
Qз = 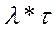 , (6.2)
, (6.2)
где: 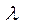 - интенсивность спроса;
- интенсивность спроса;
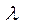 = D / 52; (6.3)
= D / 52; (6.3)
Qз = 1200/52 * 1,5 = 34,61 = 35 ед.
Таким образом, мы должны подавать заказ на пополнение, когда уровень запаса на складе снизится до 35 единиц товара.
Построим в стандартной компьютерной программе EXEL табл. 6.3 и график (рис 6.1), иллюстрирующие расчётные параметры EOQ модели.
Таблица 6.3 – Расчетные данные
| Заказы за год | Недели | Уровень максимального запаса | Точка заказа | Уровень текущего запаса |
| 6,5 | ||||
| 6,5 | ||||
| 19,5 | ||||
| 19,5 | ||||
| 32,5 | ||||
| 32,5 | ||||
| 45,5 | ||||
| 45,5 | ||||
  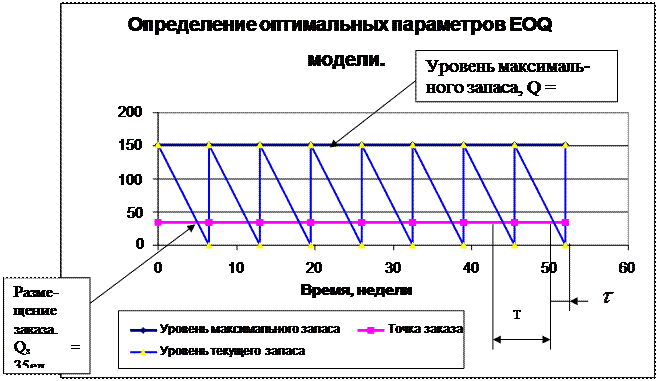 |
Рисунок 6.1 – Графическая модель работы системы управления запасами с фиксированным интервалом времени между заказами при наличии неоднократных задержках в поставках
Лабораторная работа № 7.
Нахождение оптимальной партии заказа
Цель: научиться определять оптимальную партию заказа аналитическим и графическим способом.