Пример выполнения задания. Задача.Реализовать моделирование межвидовой конкуренции при фиксированных

Задача.Реализовать моделирование межвидовой конкуренции при фиксированных значениях начальной численности популяций 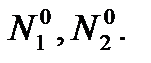Проанализировать зависимость судьбы популяций от соотношения значений параметров r₁, r₂, β₁, β₂, α₁, α₂.Выяснить, при каких условиях обе популяции выживают.

В качестве математической модели межвидовой конкуренции примем формулы (3). Исследуем модель путем нахождения особых точек на фазовой плоскости (N₁ON₂) ([6]). Как известно, судьбы популяций зависят от соотношения параметров r₁, r₂, β₁, β₂, α₁, α₂, а именно, обе популяции выживают, если на фазовой плоскости существует особая точка- устойчивый узел- c координатами 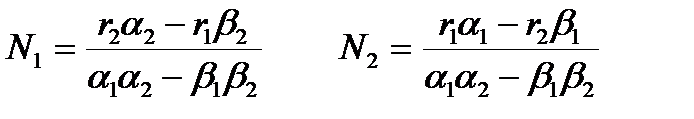. При этом выполняются следующие соотношения: 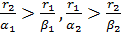. Выберем значения параметров r₁, r₂,α₁, α₂ произвольно (имея в виду, что r₁, r₂ – это числа, означающие скорость роста популяции в отсутствие конкуренции и должны иметь значения, большие единицы, а α₁, α₂ характеризуют конкуренцию, т.е. вероятность гибели особи при встрече с другой особью и должны быть меньше единицы), а параметры β₁, β₂ получим из соотношений 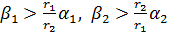. Начальные значения численности популяций 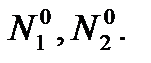возьмем, например, больше, чем координаты особой точки. Для построения таблицы значений N₁ и N₂ воспользуемся методом Эйлера решения дифференциальных уравнений (3). Из таблицы и диаграммы видно, что численности популяций уменьшаются, стремятся к особой точке и обе популяции выживают (Рис.1).

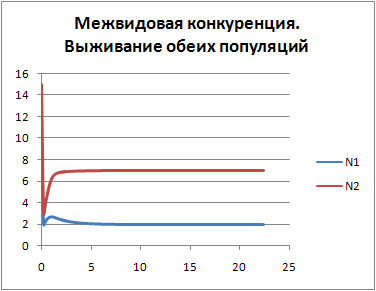
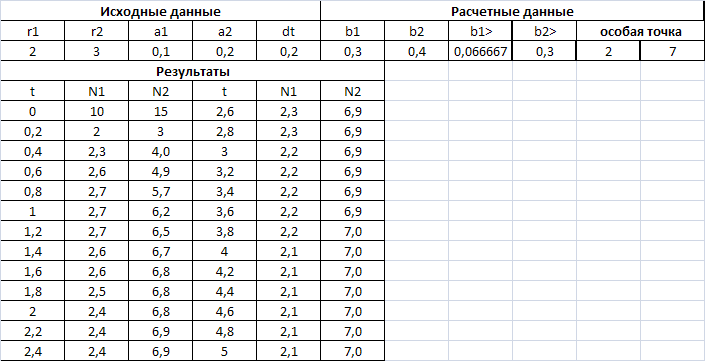Рис.1 При заданных значения входных параметров обе популяции выживают

Задание к лабораторной работе

1. Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения.

2. Спроектировать таблицу для представления результатов моделирования, предусмотрев в ней области ввода исходных данных, параметров модели и вывода результатов.

3. Выбрать метод интегрирования дифференциальных уравнений модели, разработать самостоятельно табличный алгоритм интегрирования с заданной точностью.

4. Произвести отладку и тестирование алгоритма в среде табличного процессора.

5. Выполнить конкретное задание из своего варианта работы.

6. Качественно проанализировать результаты моделирования.

7. Создать текстовый отчет по лабораторной работе, включающий:

- постановку задачи и описание модели;

- результаты тестирования программы;

- результаты, полученные в ходе выполнения задания (в различных формах);

- качественный анализ результатов.

Варианты заданий.

Вариант 1.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров b, R, N₀ в зависимости от значения параметра а. Подобрать значения а, дающие качественные различия в характере эволюции.

Вариант 2.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров a, R, N₀ в зависимости от значения параметра b в диапазоне. Подобрать значения b , дающие качественные различия в характере эволюции.

Вариант 3.

Изучить характер эволюции популяции, описываемый моделью (1), при фиксированных значениях параметров a, b, N₀ в зависимости от значения параметра R . Подобрать значения R , дающие качественные различия в характере эволюции.

Вариант 4.

Для модели (1) найти сочетания значений параметров b и R, дающих режимы монотонного и колебательного установления стационарной численности популяции изучаемой системы. Прочие параметры модели фиксированы.

Вариант 5.

Для модели (1) сочетания значений параметров b и R, дающих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов. Прочие параметры модели фиксированы.

Вариант 6.

Реализовать моделирование межвидовой конкуренции по формулам (3) при фиксированных значениях параметров r₁, r₂, β₁, β₂, α₁, α₂. Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности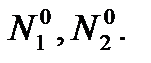

Вариант 7.

Реализовать моделирование межвидовой конкуренции по формулам (3) при значениях параметров r₁, r₂, β₁, β₂, 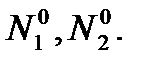. Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции a₁ и a ₂.

Вариант 8.

Подобрать значения 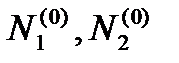обеспечивающие какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью (3)). Остальные параметры модели выбрать произвольно.

Вариант 9.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значенияхпараметров α, β, γ, δ. Проанализировать зависимость исхода эволюции от соотношения значений параметров N₀ и C₀.

Вариант 10.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значенияхпараметров α, β, γ, N₀, C₀. Проанализировать зависимость результатов моделирования от значения параметра δ.

Вариант 11.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значенияхпараметров α, β, δ, N₀, C₀. Проанализировать зависимость результатов моделирования от значения параметра γ .

Вариант 12.

Провести моделирование динамики численности популяций в системе «хищник-жертва» (модель (4)) при фиксированных значенияхпараметров β, γ, δ, N₀, C₀ . Проанализировать зависимость результатов моделирования от значения параметра α.