Задачи для самостоятельного решения. 1)Написать уравнения касательной и нормали к заданной кривой в заданной точке
1)Написать уравнения касательной и нормали к заданной кривой в заданной точке 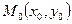 .
.
а) 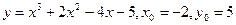 ;
;
б) 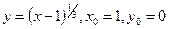 ;
;
в) 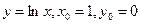 .
.
2)В какой точке касательная к параболе 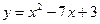
а) параллельна прямой 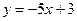 ?
?
б) перпендикулярна прямой 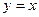 ?
?
3)Найти дифференциал 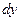 следующих функций:
следующих функций:
а) 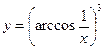 ; б)
; б) 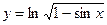 ; в)
; в) 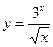 .
.
4)Вычислить приближённо:
а) 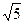 ; б)
; б) 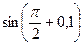 .
.
Ответы
1) а) 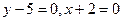 ; б)
; б) 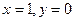 ; в)
; в) 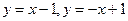 .
.
2) а) 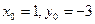 ; б)
; б) 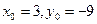 .
.
4) а) 2,25; б) 1.
Занятие №9.
Правило Лопиталя для вычисления пределов.
Производная функции, заданной параметрически.
Правило Лопиталя.
1)Пусть надо найти 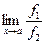 , где
, где 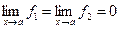 (или
(или 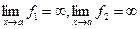 ), т.е. имеет место неопределённость вида
), т.е. имеет место неопределённость вида 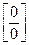 или
или 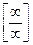 . Тогда
. Тогда
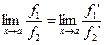 .
.
(Предполагается, что существуют производные 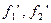 в окрестности точки
в окрестности точки 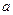 , а также существует предел, стоящий справа).
, а также существует предел, стоящий справа).
2) Пусть надо найти 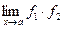 , где
, где 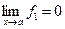 ,
, 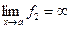 , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида 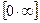 . Тогда следует сделать преобразование:
. Тогда следует сделать преобразование: 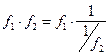 , получив неопределённость вида
, получив неопределённость вида 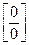 , и воспользоваться указаниями в п.1).
, и воспользоваться указаниями в п.1).
3) Пусть надо найти 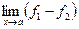 , где
, где 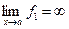 ,
, 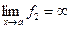 , т.е. имеется неопределённость вида
, т.е. имеется неопределённость вида 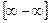 . Следует сделать подходящее преобразование выражения
. Следует сделать подходящее преобразование выражения 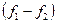 и прийти к случаю 1) или 2).
и прийти к случаю 1) или 2).
4) Пусть надо найти 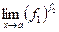 , где имеется неопределённость вида
, где имеется неопределённость вида 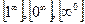 . Пользуясь свойствами логарифма, преобразуем данный предел:
. Пользуясь свойствами логарифма, преобразуем данный предел:
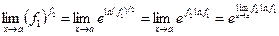
Таким образом, вычисление исходного предела сводится к вычислению предела
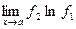 .
.
Замечание. Возможна ситуация, когда существует 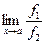 , но не существует
, но не существует 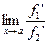 . Тогда правило Лопиталя не применимо.
. Тогда правило Лопиталя не применимо.
Производная функции, заданной параметрически
Пусть функция 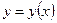 задана параметрически, т.е.
задана параметрически, т.е.
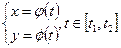 .
.
Тогда её производная 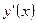 находится по следующей формуле:
находится по следующей формуле:
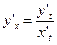 .
.
Примеры.
Найти пределы, используя правило Лопиталя:
1) 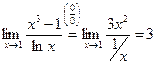 ;
;
2) 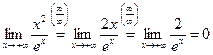 ;
;
3) 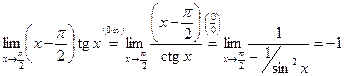 ;
;
4) 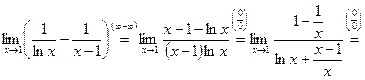
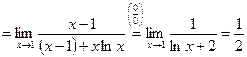 ;
;
5) 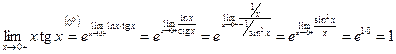 ;
;
6) 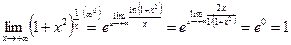 ;
;
7) 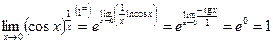 ;
;
8)Найти 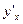 для функции
для функции 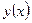 , заданной параметрически:
, заданной параметрически:
а) 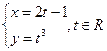 ;
;
¨ 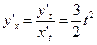 ;
;
б) 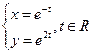 ;
;
¨ 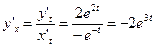 .
.
Задачи для самостоятельного решения
Найти пределы.
1) 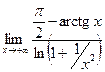 ; 2)
; 2) 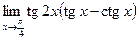 ; 3)
; 3) 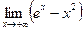 ; 4)
; 4) 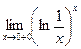 ; 5)
; 5) 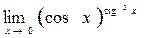 ; 6)
; 6) 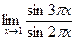 ; 7)
; 7) 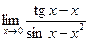 ; 8)
; 8) 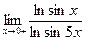 ; 9)
; 9) 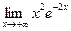 ; 10)
; 10) 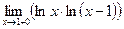 ; 11)
; 11) 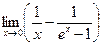 ; 12)
; 12) 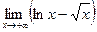 ; 13)
; 13) 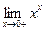 ; 14)
; 14) 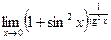 ; 15)
; 15) 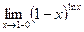 .
.
16) Найти 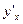 : а)
: а) 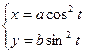 , б)
, б) 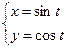 , в)
, в) 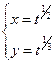 .
.
Ответы
1) 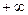 ; 2) –2; 3)
; 2) –2; 3) 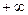 ; 4) 1; 5)
; 4) 1; 5) 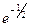 ; 6)
; 6) 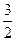 ; 7) 0; 8) 1; 9) 0; 10) 0; 11)
; 7) 0; 8) 1; 9) 0; 10) 0; 11) 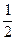 ; 12)
; 12) 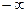 ; 13) 1; 14)
; 13) 1; 14) 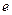 ; 15) 1; 16) а)
; 15) 1; 16) а) 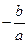 ; б)
; б) 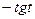 ; в)
; в) 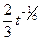 .
.
Занятие №10
Контрольная работа №2 по теме
«Производная функции одной переменной».
(Вариант-образец)
1)Написать уравнения касательной и нормали к параболе 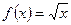 в точке с абсциссой
в точке с абсциссой 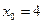 .
.
¨ Уравнения касательной и нормали в общем виде:
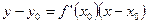 ,
, 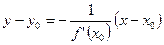 .
.
Здесь 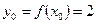 ;
; 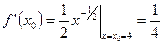 . Поэтому уравнения касательной и нормали имеют следующий вид:
. Поэтому уравнения касательной и нормали имеют следующий вид:
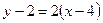 или
или 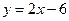 ;
;
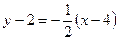 или
или 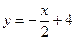 .
.
2)Найти производную 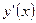 для заданной функции
для заданной функции 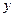 .
.
а) 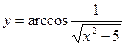 ;
;
¨ 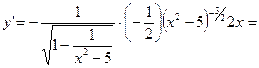
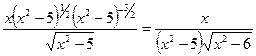 ;
;
б) 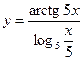 ;
;
¨ 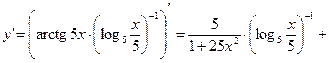
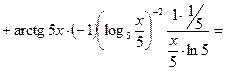
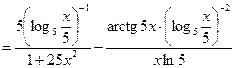 .
.
в) 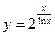 ;
;
¨ 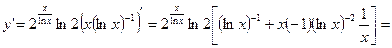
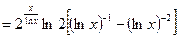 .
.
г) 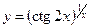 ;
;
¨ Используем логарифмическое дифференцирование: 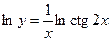 ;
;
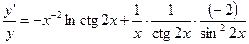 ,
,
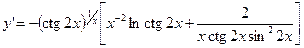 .
.
д) 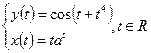
¨ Производная функции, заданной параметрически, вычисляется по формуле: 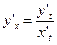 .
.
Так как здесь 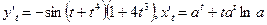 , то
, то 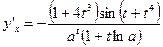 .
.
Занятие №11
Исследование функций
(нахождение интервалов возрастания/убывания функции, экстремумов, интервалов выпуклости/вогнутости, точек перегиба, асимптот графика функции)
Определение. Точка 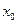 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 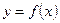 , если существует окрестность точки
, если существует окрестность точки 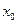 вида
вида 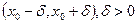 , такая что
, такая что 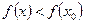
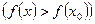 для любого х из этой окрестности. Точки максимума и минимума называются точками экстремума функции
для любого х из этой окрестности. Точки максимума и минимума называются точками экстремума функции 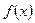 .
.
Определение. Функция 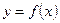 называется возрастающей (убывающей) на числовом промежутке
называется возрастающей (убывающей) на числовом промежутке 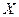 , если для
, если для 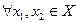 таких, что
таких, что 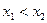 :
:
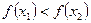
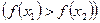 .
.
Определение. Точка 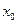 , в которой функция
, в которой функция 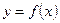 определена, но либо
определена, но либо 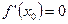 , либо
, либо 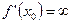 , либо
, либо 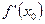 не существует, называется критической точкой 1-го рода.
не существует, называется критической точкой 1-го рода.
Как определять интервалы возрастания/убывания функции и точки экстремума:
1) Найти 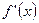 ; 2) определить критические точки 1-го рода для
; 2) определить критические точки 1-го рода для 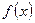 ; 3) нанести эти точки, а также точки разрыва функции, на числовую ось; 4) определить знак
; 3) нанести эти точки, а также точки разрыва функции, на числовую ось; 4) определить знак 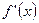 в каждом из интервалов, на которые эти точки разбивают числовую ось.
в каждом из интервалов, на которые эти точки разбивают числовую ось.
Если 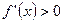
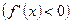 на рассматриваемом интервале, то
на рассматриваемом интервале, то 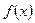 возрастает (убывает) на этом интервале. Если при переходе аргумента
возрастает (убывает) на этом интервале. Если при переходе аргумента 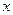 через критическую точку
через критическую точку 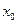 слева направо
слева направо 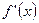 меняет знак с «+» на «—» (с «+» на «—»), то
меняет знак с «+» на «—» (с «+» на «—»), то 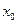 — точка максимума (минимума). Если смены знака
— точка максимума (минимума). Если смены знака 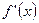 не происходит, то в точке
не происходит, то в точке 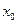 нет экстремума. Заметим, что все вышеуказанные данные можно поместить в таблицу, как это сделано в приводимых далее примерах.
нет экстремума. Заметим, что все вышеуказанные данные можно поместить в таблицу, как это сделано в приводимых далее примерах.
Примеры.
1)Найти экстремумы и интервалы возрастания (убывания) функции 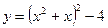 .
.
¨ Найдём 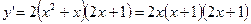 . Тогда
. Тогда 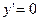 при
при 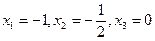 . Нанесём эти точки на числовую ось и укажем сверху знаки
. Нанесём эти точки на числовую ось и укажем сверху знаки 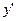 в каждом из полученных интервалов. Внизу, под осью, укажем при помощи наклонных стрелочек характер поведения функции - убывание или возрастание функции. Затем, под критическими точками
в каждом из полученных интервалов. Внизу, под осью, укажем при помощи наклонных стрелочек характер поведения функции - убывание или возрастание функции. Затем, под критическими точками 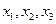 укажем, какими точками они являются — точками максимума или минимума (используя правило, данное выше).
укажем, какими точками они являются — точками максимума или минимума (используя правило, данное выше).
| x | 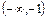 | -1 | 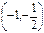 | 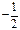 | 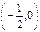 | 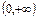 | |
| у' | — | + | — | + | |||
 y y |  | т. мин. |  | т. макс. | т. мин. |  |
2)Найти экстремумы и интервалы возрастания (убывания) функции 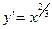 .
.
¨ Найдём 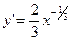 . Тогда
. Тогда 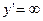 при
при 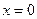 . Имеем:
. Имеем:
| x | 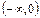 | 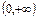 | |
| y' | — | ∞ | + |
 y y | т. мин. |  |
Определение. График функции 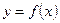 называется выпуклым (вогнутым) на
называется выпуклым (вогнутым) на 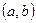 , если он расположен ниже (выше) касательной, проведённой в каждой точке
, если он расположен ниже (выше) касательной, проведённой в каждой точке 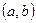 ; точка
; точка 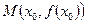 графика функции
графика функции 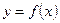 , отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Определение. Точка 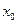 , в которой
, в которой 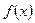 определена, но либо
определена, но либо 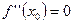 , либо
, либо 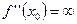 , или
, или 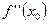 не существует, называется критической точкой 2-го рода.
не существует, называется критической точкой 2-го рода.
Как определять интервалы выпуклости (вогнутости) и точки перегиба графика функции:
1) Найти 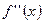 ; 2) определить критические точки 2-го рода для
; 2) определить критические точки 2-го рода для 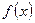 ; 3) нанести эти точки, а также точки разрыва функции, на числовую ось; 4) определить знак
; 3) нанести эти точки, а также точки разрыва функции, на числовую ось; 4) определить знак 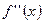 в каждом из интервалов, на которые эти точки разбивают числовую ось.
в каждом из интервалов, на которые эти точки разбивают числовую ось.
Если 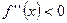
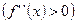 , то график функции
, то график функции 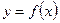 выпуклый (вогнутый) на этом интервале. Если
выпуклый (вогнутый) на этом интервале. Если 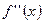 не меняет знак, то в вышеуказанной точке нет перегиба графика функции.
не меняет знак, то в вышеуказанной точке нет перегиба графика функции.
Пример.
Найти интервалы выпуклости (вогнутости) и точки перегиба графика функции 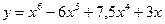 .
.
¨ 
 Найдём
Найдём 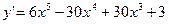 , а затем и
, а затем и 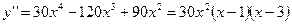 . Тогда
. Тогда 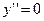 при
при 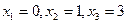 . Укажем знаки
. Укажем знаки 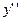 на каждом из интервалов, на которые разбивают числовую ось эти точки. Внизу, под осью, укажем особенности графика — выпуклый он или вогнутый при помощи условных знаков и , соответственно.
на каждом из интервалов, на которые разбивают числовую ось эти точки. Внизу, под осью, укажем особенности графика — выпуклый он или вогнутый при помощи условных знаков и , соответственно.
| x | 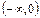 | 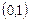 | 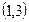 | 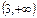 | |||
| y'’ | + | + | — | + | |||
| y | 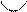 | нет пере-гиба | 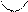 | т. пере-гиба | 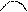 | т. пере-гиба | 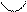 |
Определение. Асимптота графика функции 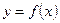 - это прямая такая, что расстояние от переменной точки
- это прямая такая, что расстояние от переменной точки 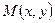 на графике до прямой стремиться к нулю при неограниченном удалении этой точки по графику от начала координат.
на графике до прямой стремиться к нулю при неограниченном удалении этой точки по графику от начала координат.
Определение. Прямая 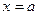 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если
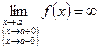
(т.е. 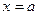 — точка разрыва 2-го рода).
— точка разрыва 2-го рода).
Определение. Прямая 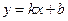 , где
, где 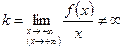 ,
, 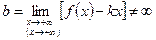 называется наклонной асимптотой. Если
называется наклонной асимптотой. Если 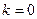 , то соответствующая прямая называется горизонтальной асимптотой.
, то соответствующая прямая называется горизонтальной асимптотой.
Пример.
Найти асимптоты графика функции: а) 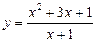 ; б)
; б) 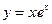 .
.
¨ а) Так как 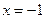 — точка разрыва 2-го рода, то
— точка разрыва 2-го рода, то 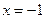 — вертикальная асимптота графика. Найдём теперь асимптоты вида
— вертикальная асимптота графика. Найдём теперь асимптоты вида 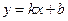 . Определим
. Определим 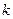 и
и 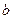 :
:
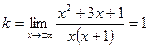 ;
; 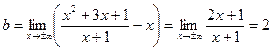 .
.
Получаем уравнение наклонной асимптоты: 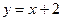 .
.
б) Вертикальных асимптот у графика нет, так как функция 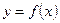 всюду непрерывна. Найдём теперь наклонные асимптоты вида
всюду непрерывна. Найдём теперь наклонные асимптоты вида 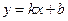 , рассматривая отдельно случаи
, рассматривая отдельно случаи 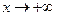 ,
, 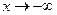 .
.
Так как при 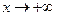
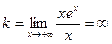 , то наклонной асимптоты при
, то наклонной асимптоты при 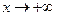 нет. При
нет. При 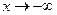
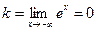 ,
, 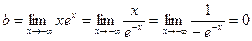 . Таким образом, уравнение наклонной (горизонтальной) асимптоты при
. Таким образом, уравнение наклонной (горизонтальной) асимптоты при 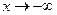 :
: 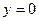 . Заметим, что для вычисления предела
. Заметим, что для вычисления предела 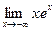 мы использовали правило Лопиталя.
мы использовали правило Лопиталя.
