По теории вероятностей
ПРИЛОЖЕНИЕ
Таблица П1
Основные вероятностные распределения
| Вид распределения | Обозна-чение | Параметры и область их изменения | Плотность распределения (дискретное распределение вероятностей) | Математическое ожидание и дисперсия |
| Равномерное | 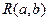 | 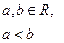 | 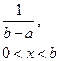 | 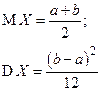 |
| Нормальное (гауссовское) | 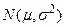 | 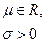 | 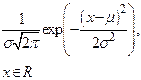 | 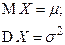 |
| Экспоненциальное (показательное) | 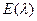 | 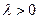 | 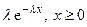 | 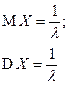 |
| Коши | 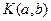 | 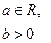 | 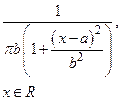 | 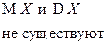 |
| Лапласа | 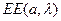 | 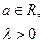 | 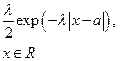 | 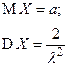 |
| Логистическое | 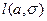 | 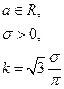 | 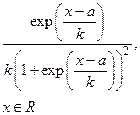 | 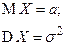 |
| Логнормальное | 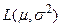 | 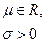 | 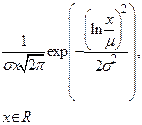 | 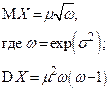 |
| Гамма-распределение | 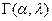 | 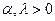 | 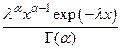 | 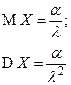 |
| Бета-распределение | 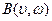 | 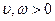 | 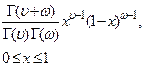 | 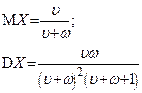 |
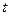 -распределение Стьюдента -распределение Стьюдента | 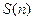 | 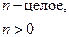 | 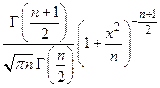 | 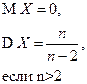 |
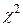 -распределение -распределение | 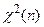 | 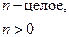 | 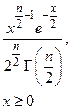 | 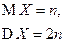 |
| Бернулли | 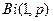 | 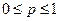 | 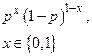 | 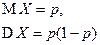 |
| Биномиальное | 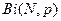 | 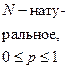 | 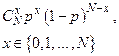 | 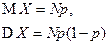 |
| Гипер-геометрическое | 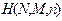 | 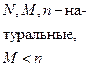 | 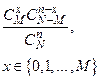 | 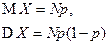 |
| Пуассона | 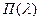 | 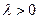 | 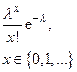 | 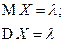 |
| Геометрическое | 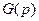 | 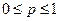 | 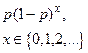 | 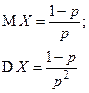 |
| Отрицательное биномиальное | 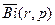 | 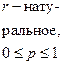 | 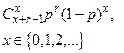 | 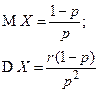 |
Таблица П2
Нормальное распределение
Квантили распределения 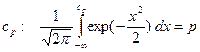 .
.
| p | 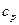 | p | 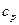 | p | 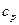 |
| 0,50 | 0.000 | 0,860 | 1,080 | 0,9910 | 2,366 |
| 0,55 | 0,126 | 0,870 | 1,126 | 0,9920 | 2,409 |
| 0,60 | 0,253 | 0,880 | 1,175 | 0,9930 | 2,457 |
| 0,65 | 0,385 | 0,890 | 1,227 | 0,9940 | 2,512 |
| 0.70 | 0,524 | 0,900 | 1,282 | 0,9950 | 2,576 |
| 0,75 | 0,674 | 0,910 | 1,341 | 0,9955 | 2,612 |
| 0,76 | 0,706 | 0,920 | 1,405 | 0,9960 | 2,652 |
| 0,77 | 0,739 | 0,930 | 1.476 | 0,9965 | 2,697 |
| 0,78 | 0,772 | 0,940 | 1,555 | 0,9970 | 2,748 |
| 0,79 | 0,806 | 0,950 | 1,645 | 0,9975 | 2,807 |
| 0,80 | 0,842 | 0,960 | 1,751 | 0,9980 | 2,878 |
| 0,81 | 0,878 | 0,970 | 1,881 | 0,9985 | 2,968 |
| 0,82 | 0,915 | 0,975 | 1,960 | 0,9990 | 3,090 |
| 0,83 | 0,954 | 0,980 | 2,051 | 0,9995 | 3,291 |
| 0,84 | 0,994 | 0,985 | 2,170 | 0,9999 | 3,720 |
| 0,85 | 1,036 | 0,990 | 2,326 | 0,99999 | 4,265 |
Примечание. Если 0<p<0.5, то 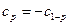 .
.
Таблица П3
Таблица значений функции 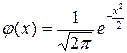
| x | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | ||||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Таблица П4
Таблица значений функции 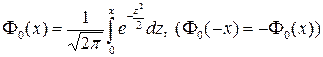
| x | ||||||||||
| 0,0 | 0,00000 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,47725 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,49865 | 3,1 | 3,2 | 3,3 | 3,4 | |||||
| 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | ||||||
| 4,0 | ||||||||||
| 4,5 | ||||||||||
| 5,0 |
Таблица П5
Таблица значений функции 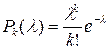
| λ k | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | ||||||
| 0,90484 | 0,81873 | 0,74082 | 0,67032 | 0,60653 | 0,54881 | 0,49659 | |||||||
| 0,09048 | 0,16375 | 0,22225 | 0,26813 | 0,30327 | 0,32929 | 0,34761 | |||||||
| 0,00452 | 0,01638 | 0,03334 | 0,05363 | 0,07582 | 0,09879 | 0,12166 | |||||||
| 0,00015 | 0,00109 | 0,00333 | 0,00715 | 0,01264 | 0,01976 | 0,02839 | |||||||
| 0,00006 | 0,00025 | 0,00072 | 0,00158 | 0,00296 | 0,00497 | ||||||||
| 0,00002 | 0,00006 | 0,00016 | 0,00036 | 0,00070 | |||||||||
| 0,00001 | 0,00004 | 0,00008 | |||||||||||
| 0,00001 | |||||||||||||
| λ k | 0,8 | 0,9 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
| 0,44933 | 0,40657 | 0,36788 | 0,13534 | 0,04979 | 0,01832 | 0,00674 | |
| 0,35946 | 0,36591 | 0,36788 | 0,27067 | 0,14936 | 0,07326 | 0,03369 | |
| 0,14379 | 0,16466 | 0,18394 | 0,27067 | 0,22404 | 0,14653 | 0,08422 | |
| 0,03834 | 0,04940 | 0,06131 | 0,18045 | 0,22404 | 0,19537 | 0,14037 | |
| 0,00767 | 0,01112 | 0,01533 | 0,09022 | 0,16803 | 0,19537 | 0,17547 | |
| 0,00123 | 0,00200 | 0,00307 | 0,03609 | 0,10082 | 0,15629 | 0,17547 | |
| 0,00016 | 0,00030 | 0,00051 | 0,01203 | 0,05041 | 0,10419 | 0,14622 | |
| 0,00002 | 0,00004 | 0,00007 | 0,00344 | 0,02160 | 0,05954 | 0,10445 | |
| 0,00001 | 0,00086 | 0,00810 | 0,02977 | 0,06528 | |||
| 0,00019 | 0,00270 | 0,01323 | 0,03627 | ||||
| 0,00004 | 0,00081 | 0,00529 | 0,01818 | ||||
| 0,00001 | 0,00022 | 0,00193 | 0,00824 | ||||
| 0,00006 | 0,00064 | 0,00343 | |||||
| 0,00001 | 0,00020 | 0,00132 | |||||
| 0,00006 | 0,00047 | ||||||
| 0,00002 | 0,00016 | ||||||
| 0,00005 | |||||||
| 0,00001 |
Таблица П6
Таблица значений функции 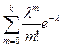
| λ k | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| 0,904837 | 0,818731 | 0,740818 | 0,670320 | 0,606531 | 0,548812 | |
| 0,995321 | 0,982477 | 0,963063 | 0,938448 | 0,909796 | 0,878099 | |
| 0,999845 | 0,998852 | 0,996390 | 0,992074 | 0,985612 | 0,977885 | |
| 0,999996 | 0,999943 | 0,999724 | 0,999224 | 0,998248 | 0,997642 | |
| 1,000000 | 0,999998 | 0,999974 | 0,999939 | 0,999828 | 0,999606 | |
| 1,000000 | 1,000000 | 0,999999 | 0,999996 | 0,999986 | 0,999962 | |
| 1,000000 | 1,000000 | 1,000000 | 1,000000 | 0,999999 | 0,999997 | |
| 1,000000 | 1,000000 | 1,000000 | 1,000000 | 1,000000 | 1,000000 |
| λ k | 0,7 | 0,8 | 0,9 | 1,0 | 2,0 | 3,0 |
| 0,496585 | 0,449329 | 0,406570 | 0,367879 | 0,135335 | 0,049787 | |
| 0,844195 | 0,808792 | 0,772483 | 0,735759 | 0,406006 | 0,199148 | |
| 0,965858 | 0,952577 | 0,937144 | 0,919699 | 0,676677 | 0,423190 | |
| 0,994246 | 0,990920 | 0,988542 | 0,981012 | 0,857124 | 0,647232 | |
| 0,999214 | 0,998589 | 0,997657 | 0,996340 | 0,947348 | 0,815263 | |
| 0,999909 | 0,999816 | 0,999658 | 0,999406 | 0,983437 | 0,916082 | |
| 0,999990 | 0,999980 | 0,999958 | 0,999917 | 0,995467 | 0,966491 | |
| 0,999998 | 0,999999 | 0,999997 | 0,999990 | 0,998904 | 0,988095 | |
| 1,000000 | 1,000000 | 1,000000 | 0,999999 | 0,999763 | 0,996196 | |
| 1,000000 | 0,999954 | 0,998897 | ||||
| 0,999992 | 0,999707 | |||||
| 0,999999 | 0,999928 | |||||
| 1,000000 | 0,999983 | |||||
| 0,999996 | ||||||
| 0,999999 | ||||||
| 1,000000 |
Предметный указатель
Аксиомы вероятности 30, 31, 1.4.4
– 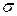 -алгебры 31
-алгебры 31
Апостериорные вероятности 43
Априорные вероятности гипотез 43
Асимметрия 2.1.76
Бернулли схема 49, 50, 54, 145, 1.6.23,
1.6.40, 3.2.1, 3.2.3, 3.2.6, 3.2.9, 3.2.20
– теорема 145
– формула 49, 54
Вероятностное пространство 31, 62, 1.4.2,
1.4.3
Вероятность 15, 65, 146
–, аксиомы 31, 1.4.4
–, геометрическое определение 25
–, классическое определение 15, 33
–, свойства 15, 18, 31, 1.4.4
– условная 30
Геометрическое определение вероятности
Гипотезы 43, 44
Дисперсия, свойство аддитивности 125
– случайного вектора 92, 2.2.26
– случайной величины 64, 2.1.4, 2.1.5
– – – дискретной 64
– – – непрерывной 64, 65, 2.1.33
– условная 94, 95, 2.2.11
– функции от случайной величины 123,
Задача Бюффона 27
– игрока де Мере 20
– композиции законов распределения
122, 123, 127, 2.3.20
– о встрече 29
Закон больших чисел 143, 149, 150, 151,
3.1.21, 3.1.23-3.1.25, 3.1.26-3.1.31
– – –, теорема Бернулли 145
– – –, – Маркова 145
– – –, – Хинчина 144, 151, 3.1.27
– – –, – Чебышева 144, 149, 3.1.18-3.1.20
– распределения 62, 66, 88, 90, 153 2.1.7,
2.1.8, 3.1.2, 3.1.19
– – арксинуса 2.1.46
– – биномиальный 3.2.20, 3.3.11
– – геометрический 71, 155
– – гипергеометрический 71
– – дискретного случайного вектора 88,
2.2.6, 2.2.9
– – дискретный 62, 65
– – Коши 156, 2.1.41
– – Лапласа 2.1.42, 2.1.76
– – непрерывного случайного вектора 90
– – непрерывный 63
Закон распределения нормальный 50
– – – двумерный 95
– – – многомерный 98
– – показательный (экспоненциальный)
2.1.84-2.1.87
– – прямоугольного треугольника 66,
2.1.38
– – Пуассона 165, 2.1.74, 2.1.78, 2.1.81,
2.1.82, 2.3.51
– – равномерный 2.1.69
– – Релея 2.1.50
– – Симпсона (закон равнобедренного
треугольника) 2.1.34, 2.1.48
– – условный 90, 2.2.11
– – функции от дискретного случайного
вектора 120, 121
– – функции от дискретной случайной
величины 119, 2.3.1-2.3.5
– – функции от непрерывного
случайного вектора 120, 121, 122
– – функции от непрерывной случайной
величины 119, 120, 2.3.6-2.3.19
Измеримая функция 62
Интегральная предельная теорема Муавра-Лапласа 50
Исходы 6, 15
– благоприятствующие 15-18, 26
– равновозможные 15, 1.2.1, 1.2.2, 1.2.14
– элементарные 6, 15
Квантиль распределения 65
Классическое определение вероятности 15,
Координаты случайного вектора 90, 91,
123, 2.2.33
Корреляционная матрица 92, 97, 103,
2.2.10
Корреляционный момент 92, 103
Коэффициент корреляции 93
Локальная предельная теорема Муавра-Лапласа 50
Маргинальные законы распределения 89
– функции распределения 88
Математическое ожидание случайной
величины 64, 2.1.4, 2.1.5
– – – – дискретной 64, 2.1.29
– – – – непрерывной 64, 2.1.33
– –, свойства 125, 2.3.84
– – случайного вектора 92, 95, 97, 98
– – – – двумерного 92
– – – – многомерного 97, 98
– – условное 93, 95
Математическое ожидание функции от случайной величины 123, 124
Медиана распределения 65, 2.1.44
Мода распределения 65, 2.1.44
Мультимодальное распределение 65
Надежность 1.4.58, 1.5.7, 1.5.26, 2.1.79
Наиболее вероятное число успехов 50
Начальный момент 65, 2.1.31
Независимые испытания 49, 50
– – с несколькими исходами 52
– случайные величины 92
Некоррелированные случайные величины
Неравенство Коши-Буняковского 125,
2.3.84
– Маркова 3.1.16
– Чебышева 143, 3.1.2-3.1.9
Операции над событиями 6
– –, произведение 6
– –, разность 6
– –, симметрическая разность 7
– –, сумма 6
Перестановка 17
Плотность вероятностей случайного
вектора 90
– – – – двумерного 90, 2.2.17, 2.2.30
– – – – многомерного 96
– – случайной величины 63, 2.1.33, 2.1.34
– – условная 91, 2.2.31
Полная группа событий 8, 1.1.13
Правило трех сигма 2.1.74
Практические рекомендации по
применению предельных теорем 52
Предельная теорема 49, 162
Производящая функция случайной
величины 153, 3.2.1-3.2.6, 3.3.11
Пространство элементарных событий 6, 8,
9, 15, 30, 31, 1.1.1-1.1.3
– вероятностное 31, 62, 1.4.2, 1.4.3
Равномерное распределение в области 94
Распределение дискретное 62
– непрерывное 63
Ряд распределения 62, 2.1.6
Свойства вероятности 15, 18, 31, 1.4.4
– плотности вероятностей случайной
величины 63
– – – случайного вектора 91
– – – – – двумерного 91
– – – – – многомерного 96
– функции распределения 62
– – – двумерной 88
– характеристической функции 154,
3.2.21-3.2.26
Свойство аддитивности дисперсии 125
– линейности математического ожидания
– «нестарения» 2.1.87
Случайная величина 62, 2.1.1, 2.1.2
– – дискретная 62, 64, 65, 2.1.6, 2.1.7,
2.1.13
– – непрерывная 63, 64, 66, 2.1.33, 2.1.34
Случайный вектор двумерный 88, 2.2.7
– – многомерный 96
– – дискретный 88
– – непрерывный 90, 94
Случайный эксперимент 6, 8, 9, 15, 25, 30
Событие 6
– достоверное 6
– невозможное 6
– противоположное 7
События 6, 145, 1.1.1, 3.1.12, 3.1.13
– независимые 32, 1.4.19
– независимые в совокупности 32
– несовместные 7
– равносильные 7
– случайные 6
– элементарные 6
Среднее квадратическое отклонение 65,
95, 2.1.4, 2.1.5, 2.1.15, 3.1.6, 3.1.10, 3.3.4
Схема Бернулли 49, 50, 54, 145, 1.6.23,
1.6.40, 3.2.1, 3.2.3, 3.2.6
– выбора без возвращения и без
упорядочивания 16
– – без возвращения, но с
упорядочиванием 17
– – с возвращением и с упорядочиванием
Сходимость по вероятности 143, 3.1.32,
3.1.34
Теорема сложения вероятностей 31, 33, 53
– Бернулли 145
– Пуассона 51, 52, 54, 1.6.29, 1.6.31-
1.6.33
– Линдеберга 163
– Ляпунова 164, 168, 3.3.8, 3.3.9
– Маркова 145
– непрерывности для производящих
функций 162
– – для характеристических функций 162
– предельная 162
– умножения вероятностей 32
– Хинчина 144, 151, 3.1.27
– Чебышева 144, 149, 3.1.18-3.1.20
Унимодальное распределение 65
Условие независимости дискретных
случайных величин 99
Условие независимости непрерывных случайных величин 97
Условие нормировки 63, 89, 96
Условная вероятность 30
Факториальный момент 153
Формула полной вероятности 43, 44
– Байеса 43, 44, 45
– Бернулли 49, 54
Функция Лапласа 53, 2.1.73
– распределения 62, 63
– –, свойства 62, 88
– – случайного вектора 88, 2.2.3, 2.2.4
– – – –, двумерная 88, 2.2.17
– – – –, многомерная 96
Характеристическая функция случайного
вектора 155, 3.3.12, 3.3.31
Характеристическая функция случайной
величины 153, 156, 3.2.7-3.2.10
Центральная предельная теорема 163, 166,
3.3.15
– – – для независимых одинаково
распределенных случайных величин 163
– – – – разнораспределенных случайных
величин: теорема Линдеберга 163;
теорема Ляпунова 164, 3.3.8, 3.3.9
Центральный момент 65, 2.1.31
Числовые характеристики функций от
случайных величин и векторов 123
Эксцесс 2.1.76
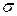 -алгебра 30, 31
-алгебра 30, 31
–, аксиомы 31
Учебное издание
Коломиец Эдуард Иванович, Дегтярев Александр Александрович
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Учебное пособие
Компьютерная верстка О.А. Дегтярева
Подписано в печать Формат 60х84 1.16.
Усл. печ. л. 11. Усл. кр.-отт. Уч.-изд. л.
Тираж 150 экз. Заказ .
Самарский государственный аэрокосмический университет
им. Академика С.П. Королева.
443086 Самара, Московское шоссе, 34.
РИО Самарского государственного
аэрокосмического университета.
443086 Самара, Московское шоссе, 34.
