Решения задачи методом потенциалов

Проверяем сбалансированность задачи:

– суммарный запас груза: 50 + 30 + 40 = 120;

– суммарные потребности: 30 + 30 + 10 + 20 = 90.

Задача несбалансированна, вводим фиктивного потребителя B_ф с потребностью 120 – 90 = 30. Для фиктивного потребителя устанавливаем стоимость, превышающую стоимость перевозок реальным потребителям. Принимаем, с_ф = 15.

Используя метод северо-западного угла, находим опорный план задачи (таблица 2.2). Суть этого метода заключается в том, что на каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполняют таким образом, что полностью выносится груз из A_i или полностью удовлетворяется потребность B_j.

Число заполненных клеток равно семи, что соответствует требуемому числу 3 + 5 – 1 = 7 (здесь 3 и 5 – количество строк и столбцов в таблице).

Таблица 2.2

Пункты отправления

Пункты назначения

Запасы

В1

В2

В3

В4

Bф

А1

А2

А3

Потребности

Стоимость перевозок без учета фиктивного потребителя составляет

S = 3∙30 + 4∙20 + 3∙10 + 1∙10 + 4∙10 + 6∙10 = 310.

Найденный опорный план проверяем на оптимальность. Находим потенциалы пунктов отправления и назначе­ния. Для этого определяем потенциалы ячеек по формуле:

p_ij = с_ij – а_i – b_j,

где с_ij – затраты на перевозку единицы груза от i-гo поставщика j-му потребителю;

а_i – потенциал i-й строки;

b_j – потенциал j-го столбца.

Потенциалы (p_ij) заполненных клеток равны нулю. Используя это свойство, получаем систему семи уравнений с восемью неизвестными:

a₁ + b₁ = 3, a₁ + b₂ = 4, a₂ + b₂ = 3, a₂ + b₃ = 1,

a₂ + b₄ = 4, a₃ + b₄ = 6, a₃ + b₅ = 15.

Полагая а₁ = 0, последовательно находим b₁ = 3, b₂ = 4, а₂ = –1, b₃ = 2, b₄ = 5, а₃ = 1, b₄ = 14.

Для каждой свободной клетки вычисляем потенциал p_ij:

р₁₃ = 2, р₁₄ = 0, р₁₅ = 1, р₂₁ = 2, р₂₅ = 2, р₃₁ = –3, р₃₂ = –1, р₃₃ = 1.

Заключаем найденные числа в рамки и записываем их в каж­дую из свободных клеток таблицы 2.3.

Таблица 2.3

Пункты отправления

Пункты назначения

Запасы

Потенциалы строк (ai)

В1

В2

В3

В4

Bф

А1

–

+

А2

–

+

–1

А3

+

–

–3

-1

Потребности

Потенциалы столбцов (bj)

Так как среди чисел p_ij имеются отрицательные, то по­строенный план перевозок не является оптимальным. Переходим к новому опорному плану. Наименьшим среди потенциалов являются р₃₁ = –3. Для данной свободной клетки строим цикл пересчета (табл. 3.3) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках рав­но 10. Клетка, в которой находится это число, становится свобод­ной в новой таблице 2.4. Далее к числам, стоящим в плюсовых клетках, добавляем 10, а из чисел, находящихся в минусовых клетках, вычтем 10 (табл. 2.4).

Число заполненных клеток равно шести, что меньше требуемого числа. Устанавливаем для клетки A₂B₂ нулевое значение загрузки.

Этот план проверяем на оптимальность. Снова находим по­тенциалы пунктов отправления и назначения. Для этого состав­ляем следующую систему уравнений:

a₁ + b₁ = 3, a₁ + b₂ = 4, a₂ + b₂ = 3, a₂ + b₃ = 1,

a₂ + b₄ = 4, a₃ + b₁ = 1, a₃ + b₅ = 15.

Полагаем a₁ = 0, последовательно получаем b₁ = 3, b₂ = 4, а₂ = –1, b₃ = 2, b₄ = 5, a₃ = –2, b₅ = 17. Для каждой свободной клетки вычисляем число р_ij; p₁₃ = 2, p₁₄ = 0, p₁₅ = –2, p₂₁ = 2, p₂₅ = –1, p₃₂ = 1, p₃₃ = 6, p₃₄ = 3.

Таблица 2.4

Пункты отправления

Пункты назначения

Запасы

Потенциалы строк (ai)

В1

В2

В3

В4

Bф

А1

–

+

20

–2

А2

–1

–1

А3

+

–

–2

Потребности

Потенциалы столбцов (bj)

Стоимость перевозок составляет

S = 3∙20 + 4∙30 + 1∙10 + 4∙20 + 1∙10 = 280.

Данный план перевозок также не являет­ся оптимальным, так как среди чисел p_ij имеются отрицательные. Поэтому переходим к новому опорному плану (табл. 2.5).

Вычислив значения потенциалов клеток, видим, что потенциалы всех свобод­ных клеток являются неотрицательными. Следова­тельно, полученный план является оптимальным. Наличие свободных ячеек с нулевыми потенциалами указывает на то, что полученный план не является единственным оптимальным планом.

Таблица 2.5

Пункты отправления

Пункты назначения

Запасы

Потенциалы строк (ai)

В1

В2

В3

В4

Bф

А1

А2

–1

А3

Потребности

Потенциалы столбцов (bj)

При данном оптимальном плане стоимость перево­зок составляет

S = 4∙30 + 1∙10 + 4∙20 + 1∙30 = 240.

Уменьшение суммарных затрат на перевозку бетона по сравнению с базовым планом составляет

∆S = 310 – 240 = 70 ед. или 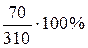= 22,6%.