Приближенное определение площади криволинейой трапеции.Риман
Первообразная функция
Функция F(х)называется первообразной функцией для функции f(х) на некотором интервале (а,b), если F/(х)= f(х), или что тоже самоеdF=f(x) dx Теорема. Если функция F(х) является первообразной функцией для функции f(х), то F(х)+С также является первообразной для f(х), где С-произвольная постоянная величина.Это следует из того, что (F(х)+С)/= F/(х)= f(х).Убедимся, что любые две первообразные F(x) и F(x) функции f(x) различаются на постоянное слагаемое. Имеем: 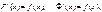
Тогда разность 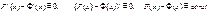
что и требовалось.
Это выражение F(х)+С называется неопределенным интегралом от функции f(х), и обозначается символом 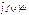 . Итак, по определению
. Итак, по определению 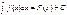 .
.
Свойства неопределенного интеграла
1) 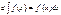 символы d и
символы d и 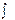 взаимно сокращаются
взаимно сокращаются
2) 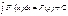 Ибо
Ибо 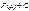 есть первообразная для
есть первообразная для 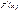
3) 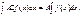
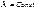
4) 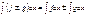
Интегрирование по частям
Метод интегрирования по частям основан на известном дифференциальном равенстве 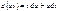 где u и v –функции от аргумента x
где u и v –функции от аргумента x
Тогда 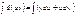
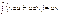 откуда
откуда 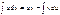 .
.
Это и есть формула интегрирования по частям.Замена переменной в неопределенном интеграле Предположим, что нам известен неопределенный интеграл
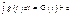 . Тогда будем иметь:
. Тогда будем иметь: 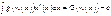 , где w(x) – произвольная дифференцируемая функция от аргумента x.
, где w(x) – произвольная дифференцируемая функция от аргумента x.
Понятие о «не берущихся» интегралах.
Существуют «берущиеся» и «не берущиеся» интегралы.
Неопределенные интегралы вида 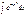 ,
, 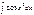 ,
, 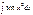 ,
, 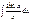 ,
,
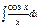 ,
, 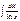 ,
, 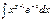 ,
, 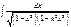 (p, k - некоторые постоянные величины), и некоторые другие не выражаются в виде конечной комбинации элементарных функций - они «не берущиеся».
(p, k - некоторые постоянные величины), и некоторые другие не выражаются в виде конечной комбинации элементарных функций - они «не берущиеся».
4 Интегрирование дробно-рациональных выражений.
от дробно-рациональных функций вида 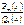 . С этой целью прежде, чем говорить об
. С этой целью прежде, чем говорить об 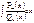 , рассмотрим элементарные (в смысле интегрирования) простые дроби (дробные выражения)
, рассмотрим элементарные (в смысле интегрирования) простые дроби (дробные выражения)
1. 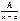 2.
2. 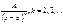 3.
3. 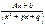 4.
4. 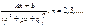
где А, a, b, р, q- вещественные числа, причем 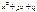 - трехчлен, не имеющий действительных корней, т.е.
- трехчлен, не имеющий действительных корней, т.е. 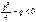 ;
; 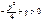
3. 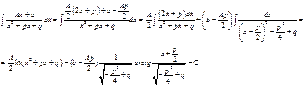
Еще прием для интегрирования таких дробных выражений:
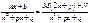 ;
; 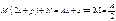 ;
; 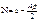 Тогда
Тогда 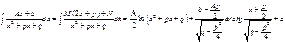
Деление в ,,уголок’’
Разложение правильных дробей Рm(х)/Qn(x) на простые. Правильная дробь – это дробь вида Рm(х)/Qn(x) , n > m. Если 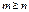 , то делением « в уголок» можно представить в виде
, то делением « в уголок» можно представить в виде 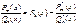 где Rk (x) – многочлен, а
где Rk (x) – многочлен, а 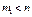 . Пусть Рm(x)/Qn(x)- правильная дробь. Разложим знаменатель на множители: Qn
. Пусть Рm(x)/Qn(x)- правильная дробь. Разложим знаменатель на множители: Qn 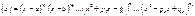 ( причем k1+k2+…..+2m1+…+2ms=n) Берем многочлен
( причем k1+k2+…..+2m1+…+2ms=n) Берем многочлен 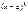 ; тогда
; тогда 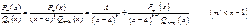 где A - постоянная, подлежащая определению, А=Соnst. Тогда
где A - постоянная, подлежащая определению, А=Соnst. Тогда
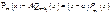 ;
; 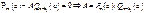 однозначно находим A, поскольку
однозначно находим A, поскольку 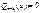 . Повторяя процедуру, находим
. Повторяя процедуру, находим
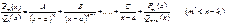 далее повторяем процедуру относительно корня b, тогда
далее повторяем процедуру относительно корня b, тогда
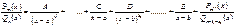 и т. д.Так можно перебрать все действительные корни.
и т. д.Так можно перебрать все действительные корни.
7 Упрощение вида Пусть 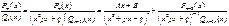 Покажем, что равенство Pm (x) – (Ax+B)Qn-2r(x) = Pm-2(x)(x2+px+q) возможно. Для этого
Покажем, что равенство Pm (x) – (Ax+B)Qn-2r(x) = Pm-2(x)(x2+px+q) возможно. Для этого
A и B определяем так, чтобы левая часть делилась на x2+px+q. Обозначим остаток от деления Рm(x) на x2+px+q чрез Мx+N, а Qn-2r(x) на x2+px+q – через Zx+K. Тогда задача сводится к подбору А и В, чтобы 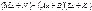 делилось нацело на x2+px+q.
делилось нацело на x2+px+q.
-АZx2+(M-ZB+Ak) x+N - BK= - AZ(x2+ 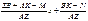 ) пропорционально x2+px+q. Делим и здесь, определяем остаток и требуем, чтобы и этот остаток обратился в нуль. Получаем:
) пропорционально x2+px+q. Делим и здесь, определяем остаток и требуем, чтобы и этот остаток обратился в нуль. Получаем:
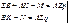 2 уравнения с двумя неизвестными A и B = ? остальные величины в этой системе известные. Можно видеть, что эта система уравнений разрешима относительно A и B.
2 уравнения с двумя неизвестными A и B = ? остальные величины в этой системе известные. Можно видеть, что эта система уравнений разрешима относительно A и B.
прежде чем интегрировать правильную дробь Pm(x)/Qn(x), ее надо представить в виде комбинации элементарных в смысле интегрирования дробей вида: 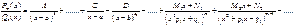
Коэффициенты A,…,С, D, …,М и т.д. удобно находить, решая систему алгебраических уравнений.
10 Интегрирование 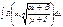
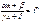 ;
; 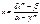 ; dx// рационально через dt Несколько более общий случай:
; dx// рационально через dt Несколько более общий случай: 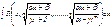
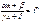 , где М – общий знаменатель
, где М – общий знаменатель 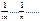
8 Дать общий вид разложения правильного дробнорационального выр-я на сумму….
Пусть многочлен, стоящий в знаменателе, удалось разложить на множители: 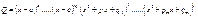 . Тогда интеграл
. Тогда интеграл 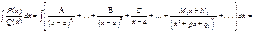 можно существенно упростить за счет следующих общих выкладок. Берем интеграл от каждого слагаемого. Так, имеем:
можно существенно упростить за счет следующих общих выкладок. Берем интеграл от каждого слагаемого. Так, имеем: 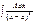 =
= 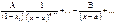 Рациональные части от всех слагаемых объединяем. Получаем в итоге равенство
Рациональные части от всех слагаемых объединяем. Получаем в итоге равенство 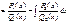 Здесь многочлены Q1(x) и Q2(x) таковы:
Здесь многочлены Q1(x) и Q2(x) таковы:
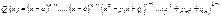
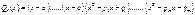
Оставшийся интеграл достаточно простой. При нахождении коэффициентов многочленов исходим из последовательности равенств: 1) 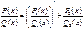 2)
2) 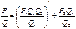 3)
3) 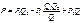
9 Интегрирование рациональных функций от sinx, cosx.
Рассмотрим неопределенный интеграл 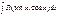 где R( , ) – рациональная функция от sin x и cos x. Этот интеграл может быть в общем случае сведен к интегралу от рациональной функции, для чего надо подставить
где R( , ) – рациональная функция от sin x и cos x. Этот интеграл может быть в общем случае сведен к интегралу от рациональной функции, для чего надо подставить 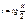 .
.
Имеем 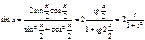
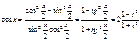
х=2arctgt 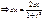
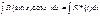
Частные случаи
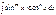
1. если 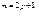 или
или 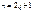 , то можно не применять универсальную подстановку. Пусть, например, m- нечетное
, то можно не применять универсальную подстановку. Пусть, например, m- нечетное
а) 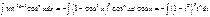
б) 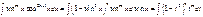
2. 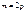 и
и 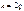 . Тогда понижаем порядок вдвое, приходим к интегралу вида
. Тогда понижаем порядок вдвое, приходим к интегралу вида 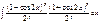 .После возведения в степени p и q и перемножения, снова имеем интегралы вида
.После возведения в степени p и q и перемножения, снова имеем интегралы вида 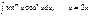 Пример
Пример
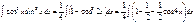 =
= 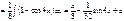
Приближенное определение площади криволинейой трапеции.Риман
Требуется определить площадь криволинейной трапеции АВСД, ограниченной сверху кривой y = f(х), слева и справа прямыми х=а и х=b и снизу прямой у = 0 (осью х). Сначала рассмотрим приближенное решение этой задачи. Разобьем [а,b] точками х0=а, х1, х2,…,хn-1, хn=b; хj-хj-1=Δ хj-1.
Проведем ординаты (вычислим) f(х0), f(х1), …, f(хn-1), f(хn).
Вычислим суммарную площадь прямоугольников высоты f(х0)…, f(хn-1)
Имеем 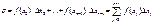
Величину σ можно рассматривать в качестве приближенного значения площади. Сумма Σ f(хj) Δхj является примером интегральной суммы.
Разбиение отрезка [а,b] можно характеризовать в данном случае максимальным значением Δхj, которое обозначим λ:
λ=max(Δxj) j=0,1,...,n-1 λ- параметр разбиения. Ему соответствует сумма площадей σ.
Возьмем более «мелкое» разбиение с параметром λ', λ'<λ . Ему соответствует сумма площадей прямоугольников: 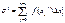 Измельчая разбиения и устремления параметра λ к нулю, получим последовательность интегральных сумм σ, σ', σ",… Если эта последовательность имеет предел при λ→0, равный S, что можно записать так
Измельчая разбиения и устремления параметра λ к нулю, получим последовательность интегральных сумм σ, σ', σ",… Если эта последовательность имеет предел при λ→0, равный S, что можно записать так 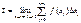 то этот предел принимают (по определению) за площадь криволинейной трапеции АВСД.
то этот предел принимают (по определению) за площадь криволинейной трапеции АВСД.
