Задача оптимизации. Некоторые математические понятия

Напомним, что множество 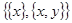называется упорядоченной парой и обозначается ещё через 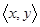. Такое название объясняется следующим свойством таких множеств:

Т е о р е м а (Теорема Куратовского)

.

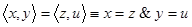Множество, все элементы которого суть упорядоченные пары, называется графиком. Иными словами, множество G есть график тогда и только тогда, когда 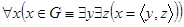. Пусть A,B оба множества. График 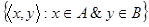называется декартовым произведением множеств A и B и обозначается через .

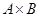Мы пишем 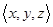вместо 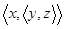и получаем упорядоченную тройку. Аналогично мы пишем 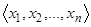вместо

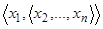и получаем упорядоченную n-ку. Если 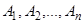все множества, символом 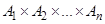обозначают множество

.

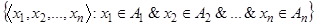Пусть А­–множество. Множество 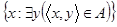называется первой проекцией множества А и обозначается через 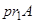, а множество 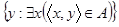называется второй проекцией множества А и обозначается через 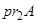. Утверждение “А есть график” эквивалентно формуле .

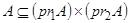График 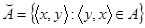называется квазиобратным (по отношению) к графику А. График А называется функциональным или однозначным, если для любых x,y,z

.

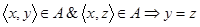График А называется инъективным, если 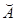функционален.

Пусть A,B–оба графики. График

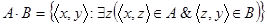
называется композицией графиков A и B и обозначается ещё через AB или 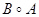. Легко показать, что композиция графиков ассоциативна, т.е. для любых трёх графиков A,B,C имеет место равенство 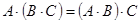. Композиция функциональных графиков есть график функциональный. Композиция инъективных графиков есть график инъективный.

Упорядоченная тройка 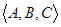множеств называется соответствием из множества А в множество B с графиком С, если имеет место включение 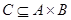. Если S есть указанное соответствие, то составляющие его множества обозначаются соответственно через 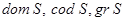и называются областью, кообластью и графиком этого соответствия. Соответствие S называется тотальным если 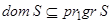. Соответствие S называется сюръективным, если 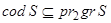. Множество 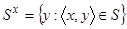называется сечением S в x. Соответствие S называется функциональным (инъективным), если таковым является график этого соответствия. Соответствие 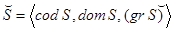называется квазиобратным к S. Функциональное и тотальное соответствие называется отображением. Сюръективное и инъективное отображение называется биективным отображением или биекцией. Отображение, кообластью которого является множество чисел, называется функционалом.

Пример 1. Пусть 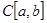означает множество непрерывных вещественных функций, заданных на отрезке 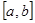. Любой функции 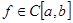однозначно соответствует число

.

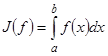Таким образом J есть функционал из множества 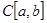в множество R вещественных чисел.

Пусть 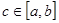. Соответствие 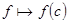, определённое на множестве 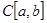, задаёт на нём вещественный функционал.