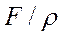Линейной неоднородной является система
Однородное дифференциальное уравнение 1 порядка решается при помощи подстановки
y=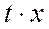 
Общим решением уравнения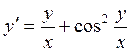 
является:
. 
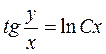
Частным решением уравнения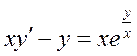 
при начальном условии y(1)=0 является:
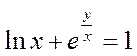
Общим решением уравнения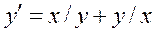 
является:
. 
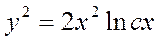
Общий вид линейного дифференциального уравнения 1 порядка есть:
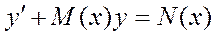
Линейным дифференциальным уравнением 1 порядка является уравнение:
. 
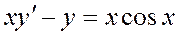
Линейное дифференциальное уравнение решается при помощи подстановки
. 
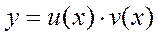
Общим решением уравнения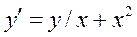 
является:
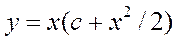
Общим решением уравнения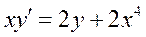 
является:
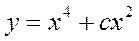
Общим видом уравнения Бернулли является:
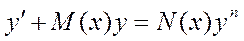
Уравнением Бернулли является уравнение
. 
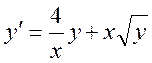
Общим решением уравнения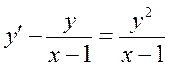 
является:
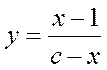
Общим решением уравнения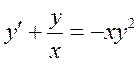 
является:
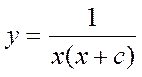
Замена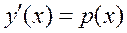 
применяется в уравнении
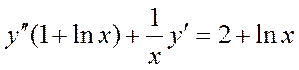
Общим решением уравнения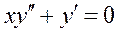 
является:
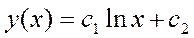
К дифференциальному уравнению вида
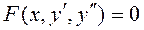относится уравнение
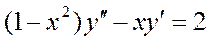
Общим решением дифференциального уравнения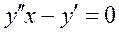 
является:
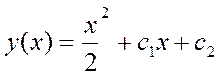
Замена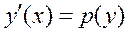 
применяется в уравнении
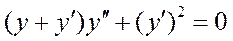
К дифференциальному уравнению вида
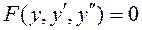относится уравнение
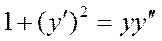
Общим решением уравнения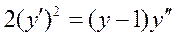 
является:
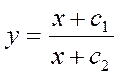
Общим решением уравнения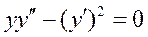 
является:
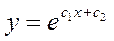
Дифференциальное уравнение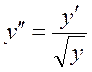 
относится к виду
. 
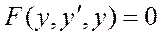
Линейным однородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение:
. 
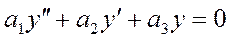
К линейному однородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
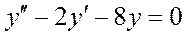
Общим решением дифференциального уравнения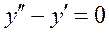 
является:
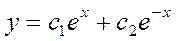
Общим решением дифференциального уравнения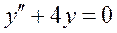 
является:
. 
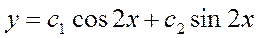
Общим решением дифференциального уравнения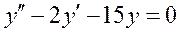 
является:
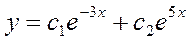
Общим решением дифференциального уравнения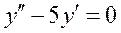 
является:
. 
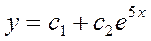
Общим решением дифференциального уравнения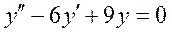 
является:
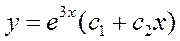
Линейным неоднородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение:
. 
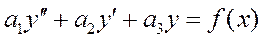
К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
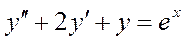
Частное решение дифференциального уравнения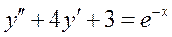 
ищется в виде:
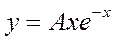
Частное решение дифференциального уравнения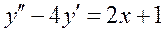 
ищется в виде:
. 
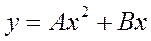
Частное решение дифференциального уравнения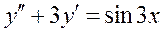 
ищется в виде:
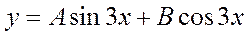
Решение дифференциального уравнения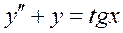 
ищется в виде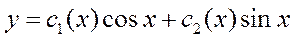 
Решение дифференциального уравнения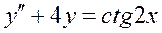 
ищется в виде 
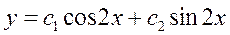, где
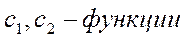
Частное решение дифференциального уравнения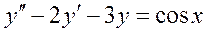 
ищется в виде:
. 
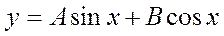
К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
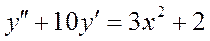Решение дифференциального уравнения 
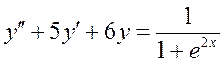ищется в виде
. 
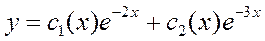
Линейной неоднородной является система
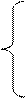
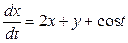
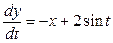В уравнении колебаний струны 
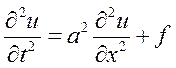a2 равно
. 
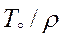
В уравнении колебаний струны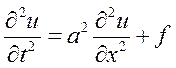 
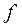равно
