Статистический критерий
Тема: Проверка статистических гипотез.
Основные понятия. Виды статистических гипотез.
На практике часто приходится на основе результатов измерений проверять различные предположения (так называемые гипотезы):
· Измерение одной и той же величины различными методами. Вопрос: Какой метод точнее?
· Лечение заболевания различными препаратами. Вопрос: Какой препарат эффективнее?
· Клиническое испытание нового препарата. Вопрос: эффективен ли препарат?
· Выявление различия между двумя выборками;
· Определение степени влияния данного фактора на результирующий показатель;
· Установление значимости полученных оценок генеральных параметров и т. д.
Определение:
Статистической гипотезой называется предположение о:
1.виде распределения;
2.значении параметра известного распределения;
3.соотношении между неизвестными параметрами случайных величин, распределённых по известному и неизвестному закону.
Классификация статистических гипотез:
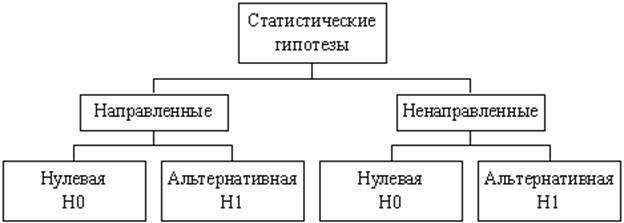
Нулевая гипотеза – это гипотеза об отсутствии различий; это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий.
Альтернативная гипотеза – это гипотеза о значимости различий; это то, что мы хотим доказать.
Ненаправленная гипотеза:
Н0: Х1 не отличается от Х2
Н1: Х1 отличается от Х2
Направленная гипотеза:
Н0: Х1 не превышает Х2
Н1: Х1 превышает Х2
Гипотезы бывают простые и сложные:
Простая:
Н0: m = 5; s – известно
Н1: m ¹ 5
Сложная:
Н0: m = 5; s – неизвестно
Н1: m ¹ 5
Направленные гипотезы формулируются, если мы заметили, что в одной группе испытуемых индивидуальные значения выше, а в другой ниже; если мы хотим доказать, что в группе А под влиянием экспериментальных условий произошли более выраженные изменения, чем в группе Б.
Статистический критерий.
Для проверки статистических гипотез используется статистический критерий К: это решающее правило, обеспечивающее надёжное поведение, т.е. принятие истинной и отклонение ложной гипотезы с высокой вероятностью. Статистический критерий – это специально подобранная величина, для которой известен (хотя бы приближённо) закон распределения.
Статистический критерий принимает в каждом случае два значения:
- эмпирическое Кэмп, рассчитанное по экспериментальным данным
- критическое Ккр, определённое по таблицам
Критическое значение статистического критерия разделяет всё множество значений критерия на две области S0 (область принятия нулевой гипотезы Н0) и S1 (область принятия альтернативной гипотезы Н1, так называемой критической области):
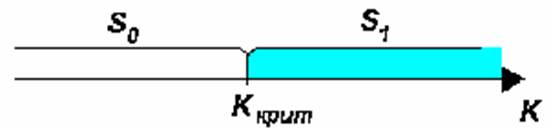
Виды критических областей:
1) двусторонняя (Довольно часто в силу симметрии закона распределения критерия Ккр1 = – Ккр2 )
2) правосторонняя
3) левосторонняя
4) односторонняя
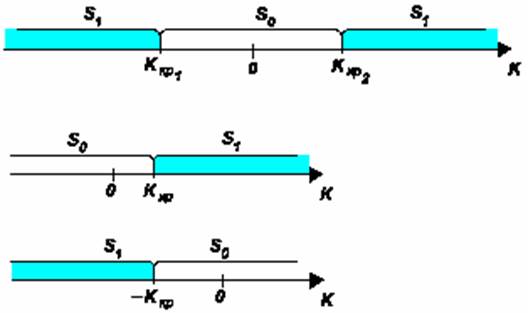
Для статистических критериев, принимающих только положительные значения, существуют двухсторонние и односторонние критические области.
Вид критической области определяется направленностью статистической гипотезы.
