Линейные уравнения и уравнение Бернулли

Уравнение вида

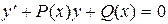(23)

называется линейным дифференциальным уравнением первого порядка, где 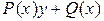- удовлетворяет условию теоремы 1.1.

Решение уравнения (23) будем искать в виде произведения некотоарых функций

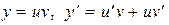, (24)

где и и v отличны от нуля. После подстановки в уравнение (23) значений у и 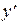, получим

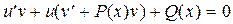. (25)

в силу произвольности выбора функций и и v, можно положить, что 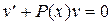. Откуда легко определяется функция v

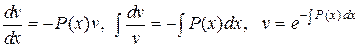. (26)

Подставив найденное решение (26) в (25), получим уравнение с разделяющимися переменными

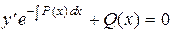, (27)

решение которого имеет вид

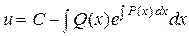. (28)

Найденные значения и и v в (24) дают окончательное решение

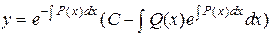. (29)

Из формулы (29) следует, что решения линейного дифференциального уравнения имеют вид

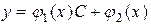, (30)

М2 Рис. 6 О С2 С С1 В2 В В1 А2 А А1 М М1 у2 у у1 Х У

т.е. у есть линейная функция произвольной постоянной.

Пусть у₁, у₂, у - различные решения, тогда отношение

,

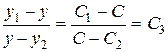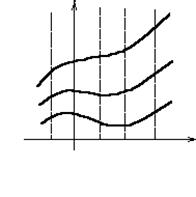
есть величина постоянная, на рис. 6 это отношения

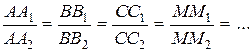
Семейство интегральных кривых линейного уравнения делит в постоянном отношении отрезок ординаты между какими-либо двумя кривыми этого семейства.

Уравнение Бернулли

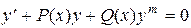(31)

является обобщением линейного дифференциального уравнения. Деление уравнения на у^т дает

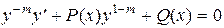. (32)

Введение вместо у новой искомой функции и вида

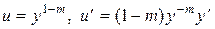
приводит к линейному дифференциальному уравнению

.

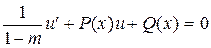Пример 1. Решить уравнение

.

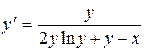Будем считать у - независимой переменной, а х - функцией, тогда

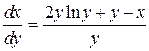
преобразуется в линейное уравнение

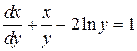. (33)

Положим х = uv, тогда (33) примет вид

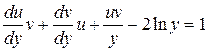. (34)

Выбираем теперь функцию v так, чтобы выполнялось равенство

,

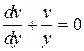отсюда

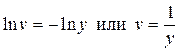. (35)

Оставшаяся часть уравнения (34) дает возможность найти функцию и, зная v - (35),

.

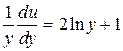Разделяя переменные и интегрируя каждую часть, получим

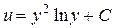. (36)

С учетом (35) и (36) решение уравнения представляет интегральную кривую вида

.

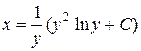Пример 2. Найти кривую, касательная к которой в точке (х_о, 2у_о) проходит через точку .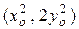

Уравнение касательной в точке (х_о, 2у_о) запишем в виде

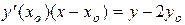. (37)

По условию точка 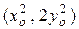удовлетворяет уравнению касательной, тогда для всех таких точек равенство (37) дает дифференциальное уравнение

,

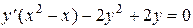(38)

представляющее собой уравнение Бернулли (т = 2).

После деления (38) на у ²

,

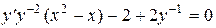вводим вместо у новую искомую функцию z = y^-1, 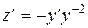, что приводит к линейному дифференциальному уравнению

.

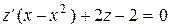Решив это линейное уравнение относительно величины z, найдем:

.

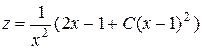Учитывая, что z = y^-1, получаем

.

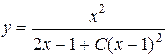[1] Изоклиной называется кривая, в каждой точке которой направления поля имеют одинаковый угловой коэффициент. Изоклина для уравнения (4) задается формулой .