Матрица исходных данных
| Периоды (наименования) наблюдений | Значение факторов | |||||
| Зависимая переменная У | Независимые переменные | |||||
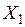 | 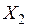 | 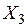 | 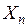 | |||
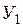 | 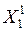 | 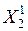 | 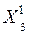 | … | 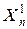 | |
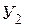 | 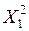 | 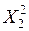 | 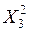 | … | 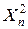 | |
| … … | 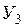 … … … … 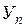 | 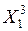 … … … … 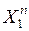 | 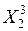 … … … … 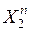 | 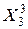 … … … … 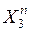 | … … | 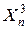 … … … … 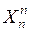 |
где: 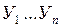 – моментные значения зависимой переменной;
– моментные значения зависимой переменной; 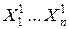 – моментные значения независимых переменных (факторов влияющих на результативный признак).
– моментные значения независимых переменных (факторов влияющих на результативный признак).
Пример конкретной матрицы приведен в таблице2.4.
Выбор зависимой (У) и независимой ( 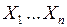 ) переменных осуществляют на основании логического анализа возможных взаимосвязей между признаками, формирующими анализируемый производственный процесс.
) переменных осуществляют на основании логического анализа возможных взаимосвязей между признаками, формирующими анализируемый производственный процесс.
В качестве результативного признака, обычно используют показатель, наиболее полно характеризующий исследуемый процесс.
Данный зависимый показатель должен иметь количественное выражение, и взят с учетом конкретных условий времени и пространства.
Не менее важным и сложным является отбор независимых факторов – аргументов. Особенностью сельскохозяйственного производства является то, что в формировании его результата (урожайности, продуктивности и т.д.) принимает участие множество факторов.
Охватить все многообразие факторов, всю сложность взаимосвязей с многочисленными случайными помехами чрезвычайно трудно, а при бесконечном множестве переменных величин задача становится неразрешимой. В связи с этим необходимо выявить наиболее существенно важные факторы, определить степень их влияния, формы взаимосвязей и установить конечное число важнейших параметров.
При корреляционном моделировании необходимо соблюдение ряда требований, предъявляемых к отбору факторов.
Во-первых, включаемые в модель факторы должны быть количественно измеримы, так как спецификой корреляционного моделирования является то, что корреляционная связь может быть выявлена только между количественно определенными признаками.
Вторым требованием является включение в модель только важнейших факторов, оказывающих наиболее существенное влияние на процесс производства.
Следующее требование заключается в том, что факторы, вошедшие в модель не должны находиться между собой и зависимым фактором в функциональной связи. Например, при построении корреляционной модели урожайности в качестве факторов-аргументов не стоит включать размер посевных площадей и объём валового сбора, так как нет смысла выявлять корреляционную связь там, где проявляется функциональный характер.
Важным требованием является не включение в модель факторов, косвенно дублирующих друг друга, или когда один фактор является частью другого, а также факторы, представляющие собой промежуточный результат по отношению к другим факторам.
Несоблюдение этих условий приведет к тому, что факторы неправильно включенные, могут исказить фактическое влияние остальных факторов, показать недостоверную и возможно даже отрицательную эффективность, что в конечном счете ведет к ошибочным выводам.
Таблица 14
